Characteristics of a Normal Distribution

In our earlier discussion of descriptive statistics, we introduced the mean as a measure of central tendency and variance and standard deviation as measures of variability. We can now use these parameters to answer questions related to probability.

For a normally distributed variable in a population the mean is the best measure of central tendency, and the standard deviation(s) provides a measure of variability.

The notation for a sample from a population is slightly different:

 

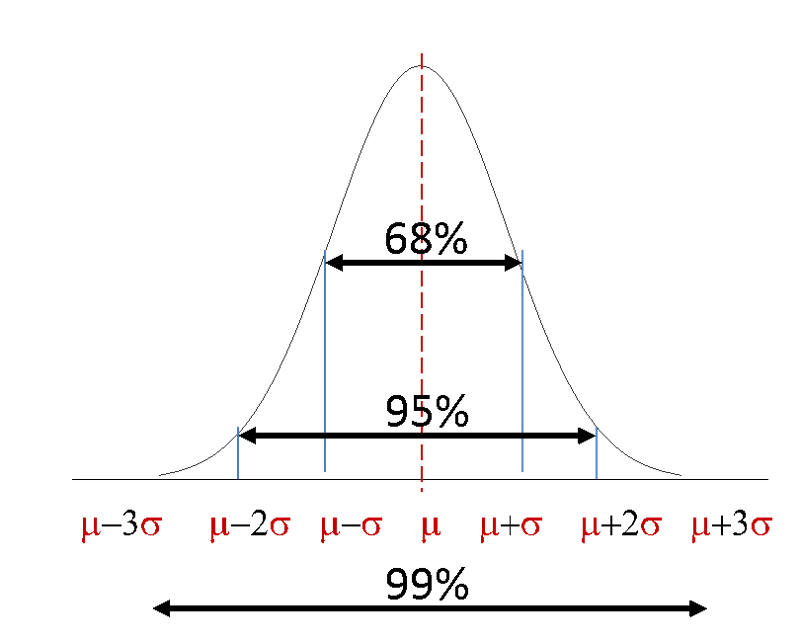
We can use the mean and standard deviation to get a handle on probability. It turns out that, as demonstrated in the figure below,

There are many variables that are normally distributed and can be modeled based on the mean and standard deviation. For example,

The ability to address probability is complicated by having many distributions with different means and different standard deviations. The solution to this problem is to project these distributions onto a standard normal distribution that will make it easy to compute probabilities.

The Standard Normal Distribution

The standard normal distribution is a special normal distribution that has a mean=0 and a standard deviation=1. This is very useful for answering questions about probability, because, once we determine how many standard deviations a particular result lies away from the mean, we can easily determine the probability of seeing a result greater or less than that.

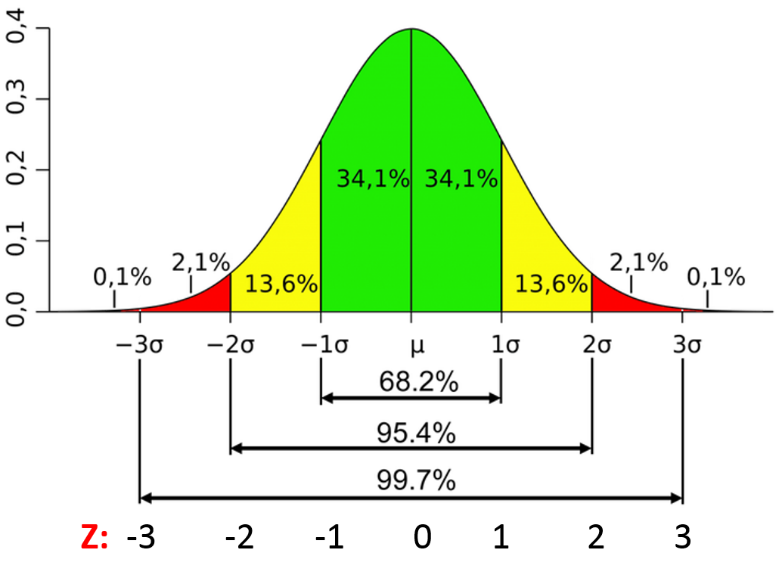
The figure below shows the percentage of observations that would lie within 1, 2, or 3 standard deviations from any mean in a distribution that is more or less normally distributed. For a given value in the distribution, the Z score is the number of standard deviations above or below the mean. We can think about probability from this.

Example:
What is the probability of a Z score less than 0?   Answer: P= 34.1+13.6+  2.1+0.1=50%
What is the probability of a Z score less than +1? Answer: P= 34.1+34.1+13.6+2.1+0.1=84%

How many standard deviation units a given observation lies above or below the mean is referred to as a Z score, and there are tables and computer functions that can tell us the probability of a value less than a given Z score.

For example, in R:

> pnorm(0)
[1] 0.5

The probability of an observation less than the mean is 50%.


 > pnorm(1)
[1] 0.8413447

The probability of an observation less than 1 standard deviation above the mean is 84.13%.

We can also look up the probability in a table of Z scores:

So, for any distribution that is more or less normally distributed, if we determine how many standard deviation units a given value is away from the mean (i.e., its corresponding Z score), then we can determine the probability of a value being less than or greater than that.

It is easy to determine how many SD units a value is from the mean of a normal distribution:

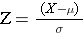
In other words, we determine how far a given value is from the mean and then divide that by the standard deviation to determine the corresponding Z score.

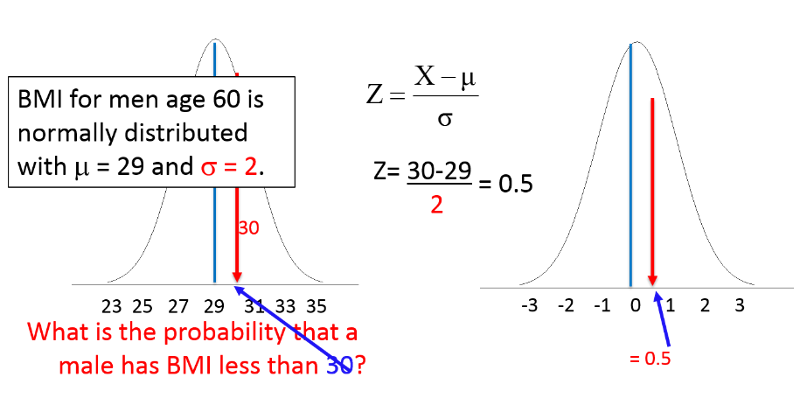
For example, BMI among 60 year old men is normally distributed with µ=29 and σ=6. What is the probability that a 60 year old male selected at random from this population will have a BMI less than 30? Stated another way, what proportion of the men have a BMI less than 30?

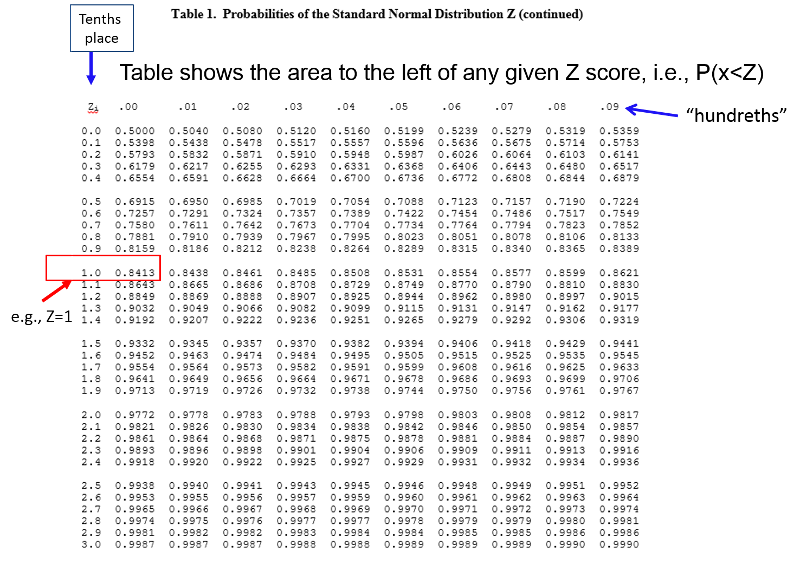
BMI=30 is just 0.17 SD units above the mean of 29. So, all we have to do is look up 0.17 in the table of Z scores to see what the probability of a value less than 30 is. Note that the table is set up in a very specific way. The entries in the middle of the table are areas under the standard normal curve BELOW the z score. The z score can be found by locating the units and tenths place along the left margin and the hundredths place across the top row.

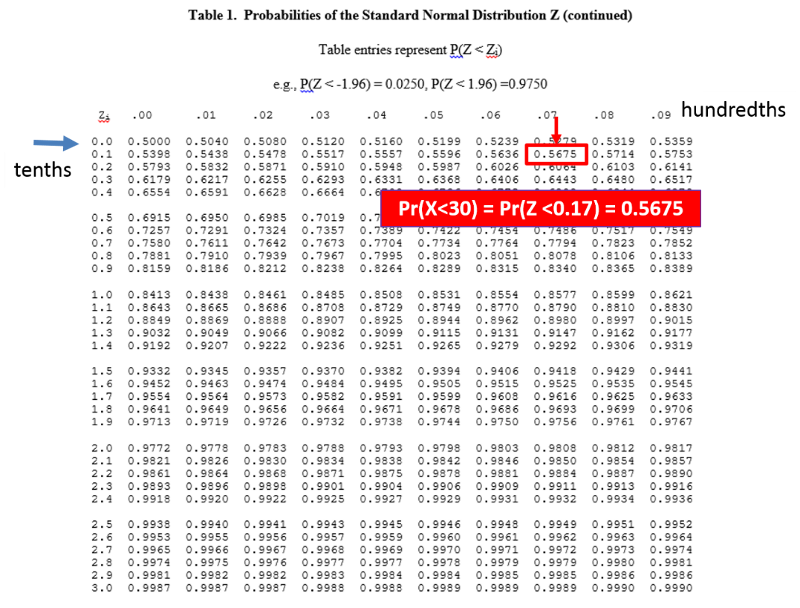
From the table of Z scores we can see that Z=0.17 corresponds to a probability of 0.5676.

We can also look up the probability using R:

>pnorm(0.17)
[1] 0.5674949

You can also have R automatically do the calculation of the Z score and look up the probability by using the pnorm function with the parameters (the value, the mean, and the standard deviation), e.g.:

# Use "pnorm(x,mean,SD)"
>pnorm(30,29,6)
[1] 0.5661838

The table of probabilities for the standard normal distribution gives the area (i.e., probability) below a given Z score, but the entire standard normal distribution has an area of 1, so the area above a Z of 0.17 = 1-0.5675 = 0.4325.

You can compute the probability above the Z score directly in R:

>1-pnorm(0.17)
[1] 0.4325051

A Slightly Different Example:

Now consider what the probability of BMI<30 would be in a slightly different population with the same mean (29), but less variability, with standard deviation=2. This distribution is narrower, so values less than 30 should represent a slightly greater proportion of the population.

Using the same equation for Z:

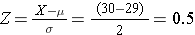
Conclusion: In this population 69% of men who are 60 years old will have BMI<30.

Test Yourself

Problem #1

BMI among 60 year old men is normally distributed with µ=29 and σ=6. What is the probability that a 60 year old male selected at random from this population will have a BMI less than 40?

Answer

Problem #2

In the same population of 60 year old men with µ=29 and σ=6. What is the probability that a male age 60 has BMI greater than 40?

Answer

Problem #3

In the same population of 60 year old men with µ=29 and σ=6. What is the probability that a 60 year old male selected at random from this population will have a BMI between 30 and 40?

Answer in a Word file

What if Z is a Negative Number?

Suppose I want to know what proportion of 60 year old men have BMI less than 25 in my population with µ=29 and σ=6. I compute the Z score as follows:

Z=(x-µ)/σ = (25-29)/6 = -0.6661

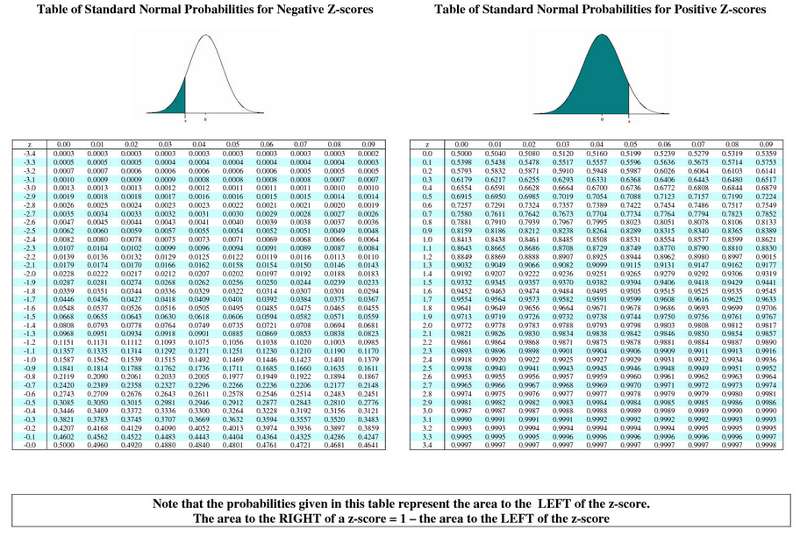
Here the value of interest is below the mean, so the Z score is negative. The full table of Z scores takes this into account as shown below. Note that the left page of the table has negative Z scores for values below the mean, and the page on the right has corresponding positive Z scores for values above the mean. In both cases the probability is the area to the left of the Z score.

If we use the left side of the table below and look up the probability for Z=-0.6661, the probability is about 0.2546.

Alternatively, we can use R to compute the probability as follows:

> pnorm(-0.666)
[1] 0.2527056

 

 


return to top | previous page | next page