The Subjects
Population Hierarchy
When clinical trials are performed there is generally a target population or reference population to which one would like to apply the findings. For example, researchers reported on the efficacy of low-dose aspirin in preventing myocardial infarction in women [Ridker P, et al.: A randomized trial of low-dose aspirin in the primary prevention of cardiovascular disease in women. N Engl J Med 2005;352:1293-304]. The reference population was adult females who have not had a myocardial infarction.
The experimental population (study population) are the potential participants, i.e., a practical subset of people who are representative of the reference population. Important practical considerations might include choosing a group that was sufficiently large and likely to produce an adequate number of end points (outcomes of interest) in order to allow valid statistical analysis and a reasonably precise estimate of the measure of effect. The participants would be those who were willing to participate (i.e., consented after being fully informed about the study) and also met eligibility criteria that take into account scientific and safety considerations. For example, an inclusion criterion
might be age 45 or older in order to achieve a study sample that would produce a sufficient number of end points. In a study of the effect of aspirin on cardiovascular disease it would also be important to specify exclusion criteria, e.g., people with pre-existing cardiovascular disease or those who were already taking aspirin or anticoagulants for other medical conditions.
The following is an excerpt from the report by Ridker et al. describing how they obtained their study population:
|
"In brief, between September 1992 and May 1995, letters of invitation were mailed to more than 1.7 million female health professionals. A total of 453,787 completed the questionnaires, with 65,169 initially willing and eligible to enroll. Women were eligible if they were 45 years of age or older; had no history of coronary heart disease, cerebrovascular disease, cancer (except non-melanoma skin cancer), or other major chronic illness; had no history of side effects to any of the study medications; were not taking aspirin or nonsteroidal anti-inflammatory medications (NSAIDs) more than once a week (or were willing to forego their use during the trial); were not taking anticoagulants or corticosteroids;
|
Eligible women were enrolled in a three-month run-in phase of placebo administration to identify a group likely to be compliant with long-term treatment. A total of 39,876 women were willing, eligible, and compliant during the run-in period and underwent randomization: 19,934 were assigned to receive aspirin and 19,942 to receive placebo."
Internal and External Validity
The eligibility criteria need to balance the needs for internal and external validity. Internal validity refers to the accuracy of the conclusions within that particular study sample, while external validity refers to whether or not the results of a particular study are relevant to a more general population. For example, in 1981 the Physicians Health Study sent invitation letters, consent forms, and enrollment questionnaires to all 261,248 male physicians between 40 and 84 years of age who lived in the United States and who were registered with the American Medical Association. Less than half responded to the invitation, and only about 59,000 were willing to participate. Of those 33,223 were both willing and eligible.
These physicians were enrolled in a run-in phase during which all received active aspirin and placebo beta-carotene (both of these were to be tested in a two-by-two factorial design, to be described later in this module). After 18 weeks, participants were sent a questionnaire asking about their health status, side effects, compliance, and willingness to continue in the trial. A total of 11,152 changed their minds, reported a reason for exclusion, or did not reliably take the study pills. The remaining 22,071 physicians were then randomly assigned to experimental groups and followed for the duration of the study. The study was restricted to physicians in order to facilitate follow-up, since all subjects were registered physicians in the AMA. The study excluded female physicians, because in 1981 the number of registered female physicians over the age of 40 was quite small and would not have provided enough statistical power to provide valid results in females. (Note that the exclusion of females is not an example of selection bias. It does not affect the validity of the results of the study but rather the nature of the target population and therefore the generalizability of the results.) The study convincingly demonstrated that the regimen of low-dose aspirin reduced the risk of myocardial infarction (heart attack) in these subjects by about 44%, and the results were reported in 1989 in the New England Journal of Medicine. However, one of the unanswered questions was whether the results were applicable to females (or even to the non-physician population at large). Consequently, the questions about the external validity, i.e. the generalizability, of the study lingered and eventually led to a separate clinical trial in The Women's Health Study. The results were published in 2005 and concluded:
|
"In this large, primary-prevention trial among women, aspirin lowered the risk of stroke without affecting the risk of myocardial infarction or death from cardiovascular causes, leading to a non-significant finding with respect to the primary end point."
Ridker et al.: A randomized trial of low-dose aspirin in the primary prevention of cardiovascular disease in women. N Engl J Med 2005;352:1293-304. |
In other words, the effect of aspirin in preventing myocardial infarctions did appear to be different in women and men.
Sample Size
The major advantage of large randomized clinical trials is that that they are the most effective way to reduce confounding. As such, they offer the opportunity to identify small to moderate effects that may be clinically very important. For example, coronary artery disease (CAD) is the most frequent cause of death and disability in the the US and worldwide. Consequently, interventions that reduce risk by 15-20% would be extremely important, because so much death and disability is attributed to CAD. While control of confounding makes it easier to accurately assess modest but important effects, it is still necessary to have an adequate sample size in order to produce a measure of association that is reasonably precise. If the study does not have a sufficient sample size (i.e., if it is "under powered"), the study might fail to identify a meaningful benefit that truly existed, and much time and money would have been wasted on an incorrect conclusion.
Actually, the key factor influencing the power of the study is the number of outcomes (often referred to as "endpoints") rather than study size per se. Of course, increasing study size will increase the number of endpoints, but two other factors that affect the power of the study are the likelihood of the outcome among the study subjects and the duration of the study. For example, both the Physicians' Health Study and the Women's Health Study required participants to be above the age of 40 at the time of enrollment, since younger subjects would be substantially less likely to have a myocardial infarction during the planned follow up period. The duration of the follow up period is obviously also relevant, since shorter periods of follow up will produce fewer events and reduce statistical power
In order to avoid conducting studies that are underpowered, investigators will perform a series of calculations referred to as sample size estimates. This is not a single calculation, but a series of calculations that, in essence, address "what if" questions. For example, the observational studies that led up to the Physicians Health Study failed to find statistically significant benefits of aspirin, but they seemed to suggest that if there were a benefit, it would likely be on the order of a 15-30% reduction in risk of myocardial infarction. If one has estimates of the magnitude of risk (the expected cumulative incidence) in the reference population, one can than perform calculations to estimate how many subjects one would need in each of two study groups to detect a given effect, if it existed. For example, if the expected incidence of myocardial infarction over five years in males over 40 years of age were around 5%, and if low-dose aspirin truly reduced the risk by about 20%, then the expected frequencies in the untreated placebo group and the aspirin treated group would be expected to be 0.05 and 0.04 respectively. The Excel file "Epi_Tools.XLS" has a worksheet entitled "Sample Size" that performs these calculations for you.
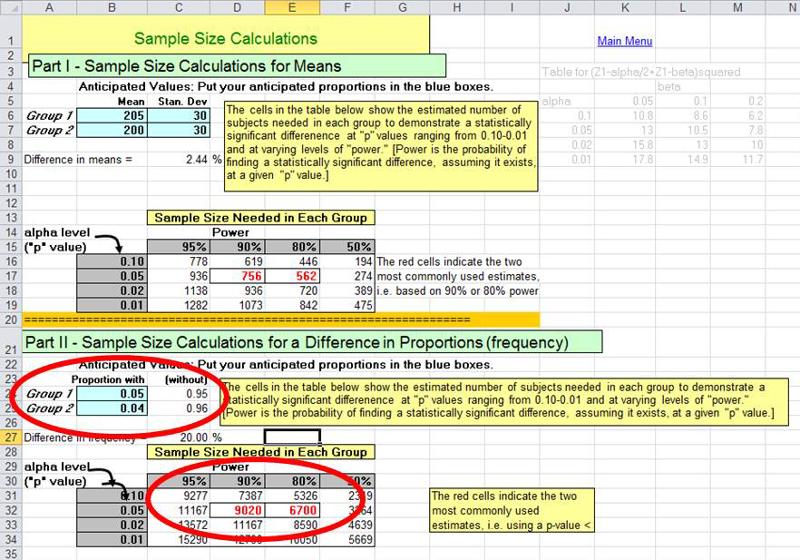
The illustration above shows that a "what if" situation, i.e. what if the frequency of myocardial infarction is 5% without aspirin and 4% with the low-dose aspirin regimen (i.e., a 20% reduction in risk). The calculations indicate that in order to have a 90% probability (statistical power) of finding a statistically significant difference using p<0.05 as the criterion of significance, we would need a little over 9,000 subjects in each group. The investigators in the Physicians' Health Study wisely sought a somewhat larger sample than the estimates indicated.