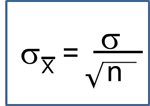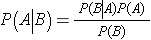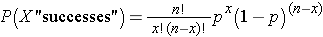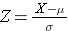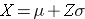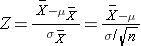Summary

In this learning module we discussed probability as it applies to selecting individuals from a population into a sample. There are certain options available when the entire population can be enumerated. However, when the population enumeration is not available, probability models can be used to determine probabilities as long as certain conditions are satisfied. The binomial and normal distribution models are popular models for discrete and continuous outcomes, respectively.

The Central Limit Theorem is very important in biostatistics, because it brings together the concepts of probability and inference. As a result, the Central Limit Theorem will be very important in later modules. 

Key Formulas and Concepts in Probability

Concept

 Formula

Basic Probability

 P(Characteristic) = # persons with characteristic / N
  • Sensitivity
  • Specificity False Positive Fraction
  • False Negative Fraction Positive Predictive Value
  • Negative Predictive Value
  • P(Screen Positive | Disease)
  • P(Screen Negative | Disease Free) P(Screen Positive | Disease Free)
  • P(Screen Negative | Disease) P(Disease | Screen Positive)
  • P(Disease Free | Screen Negative)
Independent Events

P(A|B) = P(A)

or

P(A and B) = P(A)ּP(B)

Bayes's Theorem

Binomial Distribution

Standard Normal Distribution

Percentiles of the Normal Distribution

Application of Central Limit Theorem

 


return to top | previous page | next page