Sample Sizes for Two Independent Samples, Continuous Outcome
In studies where the plan is to perform a test of hypothesis comparing the means of a continuous outcome variable in two independent populations, the hypotheses of interest are:

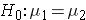
versus

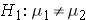
where μ 1 and μ 2 are the means in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is:

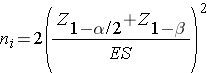
where ni is the sample size required in each group (i=1,2), α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α /2 below it, and 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as:

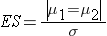
where | μ 1 - μ 2 | is the absolute value of the difference in means between the two groups expected under the alternative hypothesis, H1. σ is the standard deviation of the outcome of interest. Recall from the module on Hypothesis Testing that, when we performed tests of hypothesis comparing the means of two independent groups, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome.
Sp is computed as follows:

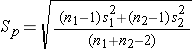
If data are available on variability of the outcome in each comparison group, then Sp can be computed and used to generate the sample sizes. However, it is more often the case that data on the variability of the outcome are available from only one group, usually the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that may have involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated.
Note also that the formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used (see Howell3 for more details).
Example 9:
An investigator is planning a clinical trial to evaluate the efficacy of a new drug designed to reduce systolic blood pressure. The plan is to enroll participants and to randomly assign them to receive either the new drug or a placebo. Systolic blood pressures will be measured in each participant after 12 weeks on the assigned treatment. Based on prior experience with similar trials, the investigator expects that 10% of all participants will be lost to follow up or will drop out of the study. If the new drug shows a 5 unit reduction in mean systolic blood pressure, this would represent a clinically meaningful reduction. How many patients should be enrolled in the trial to ensure that the power of the test is 80% to detect this difference? A two sided test will be used with a 5% level of significance.
In order to compute the effect size, an estimate of the variability in systolic blood pressures is needed. Analysis of data from the Framingham Heart Study showed that the standard deviation of systolic blood pressure was 19.0. This value can be used to plan the trial.
The effect size is:

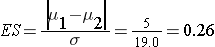
We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

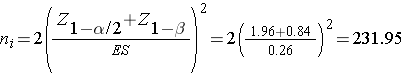
Samples of size n1=232 and n2= 232 will ensure that the test of hypothesis will have 80% power to detect a 5 unit difference in mean systolic blood pressures in patients receiving the new drug as compared to patients receiving the placebo. However, the investigators hypothesized a 10% attrition rate (in both groups), and to ensure a total sample size of 232 they need to allow for attrition.
N (number to enroll) * (% retained) = desired sample size
Therefore N (number to enroll) = desired sample size/(% retained)
N = 232/0.90 = 258.
The investigator must enroll 258 participants to be randomly assigned to receive either the new drug or placebo.

An investigator is planning a study to assess the association between alcohol consumption and grade point average among college seniors. The plan is to categorize students as heavy drinkers or not using 5 or more drinks on a typical drinking day as the criterion for heavy drinking. Mean grade point averages will be compared between students classified as heavy drinkers versus not using a two independent samples test of means. The standard deviation in grade point averages is assumed to be 0.42 and a meaningful difference in grade point averages (relative to drinking status) is 0.25 units. How many college seniors should be enrolled in the study to ensure that the power of the test is 80% to detect a 0.25 unit difference in mean grade point averages? Use a two-sided test with a 5% level of significance.
Sample Size for Matched Samples, Continuous Outcome
In studies where the plan is to perform a test of hypothesis on the mean difference in a continuous outcome variable based on matched data, the hypotheses of interest are:

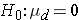
versus

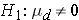
where μd is the mean difference in the population. The formula for determining the sample size to ensure that the test has a specified power is given below:

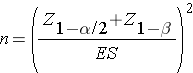
where α is the selected level of significance and Z1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, 1- β is the selected power and Z1-β is the value from the standard normal distribution holding 1- β below it and ES is the effect size, defined as follows:

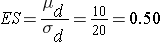
where μd is the mean difference expected under the alternative hypothesis, H1, and σd is the standard deviation of the difference in the outcome (e.g., the difference based on measurements over time or the difference between matched pairs).
Example 10:
An investigator wants to evaluate the efficacy of an acupuncture treatment for reducing pain in patients with chronic migraine headaches. The plan is to enroll patients who suffer from migraine headaches. Each will be asked to rate the severity of the pain they experience with their next migraine before any treatment is administered. Pain will be recorded on a scale of 1-100 with higher scores indicative of more severe pain. Each patient will then undergo the acupuncture treatment. On their next migraine (post-treatment), each patient will again be asked to rate the severity of the pain. The difference in pain will be computed for each patient. A two sided test of hypothesis will be conducted, at α =0.05, to assess whether there is a statistically significant difference in pain scores before and after treatment. How many patients should be involved in the study to ensure that the test has 80% power to detect a difference of 10 units on the pain scale? Assume that the standard deviation in the difference scores is approximately 20 units.
First compute the effect size:

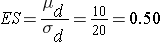
Then substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

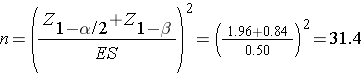
A sample of size n=32 patients with migraine will ensure that a two-sided test with α =0.05 has 80% power to detect a mean difference of 10 points in pain before and after treatment, assuming that all 32 patients complete the treatment.
Sample Sizes for Two Independent Samples, Dichotomous Outcomes
In studies where the plan is to perform a test of hypothesis comparing the proportions of successes in two independent populations, the hypotheses of interest are:
H0: p1 = p2 versus H1: p1 ≠ p2
where p 1 and p2 are the proportions in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is given below:

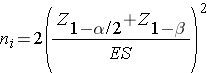
where ni is the sample size required in each group (i=1,2), α is the selected level of significance and Z1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, and 1- β is the selected power and Z1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as follows:

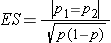 ,
,
where |p1 - p2| is the absolute value of the difference in proportions between the two groups expected under the alternative hypothesis, H1, and p is the overall proportion, based on pooling the data from the two comparison groups (p can be computed by taking the mean of the proportions in the two comparison groups, assuming that the groups will be of approximately equal size).
Example 11:
An investigator hypothesizes that there is a higher incidence of flu among students who use their athletic facility regularly than their counterparts who do not. The study will be conducted in the spring. Each student will be asked if they used the athletic facility regularly over the past 6 months and whether or not they had the flu. A test of hypothesis will be conducted to compare the proportion of students who used the athletic facility regularly and got flu with the proportion of students who did not and got flu. During a typical year, approximately 35% of the students experience flu. The investigators feel that a 30% increase in flu among those who used the athletic facility regularly would be clinically meaningful. How many students should be enrolled in the study to ensure that the power of the test is 80% to detect this difference in the proportions? A two sided test will be used with a 5% level of significance.
We first compute the effect size by substituting the proportions of students in each group who are expected to develop flu, p1=0.46 (i.e., 0.35*1.30=0.46) and p2=0.35 and the overall proportion, p=0.41 (i.e., (0.46+0.35)/2):

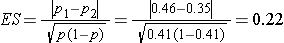
We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.

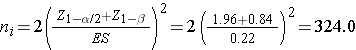
Samples of size n1=324 and n2=324 will ensure that the test of hypothesis will have 80% power to detect a 30% difference in the proportions of students who develop flu between those who do and do not use the athletic facilities regularly.

Donor Feces? Really? Clostridium difficile (also referred to as "C. difficile" or "C. diff.") is a bacterial species that can be found in the colon of humans, although its numbers are kept in check by other normal flora in the colon. Antibiotic therapy sometimes diminishes the normal flora in the colon to the point that C. difficile flourishes and causes infection with symptoms ranging from diarrhea to life-threatening inflammation of the colon. Illness from C. difficile most commonly affects older adults in hospitals or in long term care facilities and typically occurs after use of antibiotic medications. In recent years, C. difficile infections have become more frequent, more severe and more difficult to treat. Ironically, C. difficile is first treated by discontinuing antibiotics, if they are still being prescribed. If that is unsuccessful, the infection has been treated by switching to another antibiotic. However, treatment with another antibiotic frequently does not cure the C. difficile infection. There have been sporadic reports of successful treatment by infusing feces from healthy donors into the duodenum of patients suffering from C. difficile. (Yuk!) This re-establishes the normal microbiota in the colon, and counteracts the overgrowth of C. diff. The efficacy of this approach was tested in a randomized clinical trial reported in the New England Journal of Medicine (Jan. 2013) . The investigators planned to randomly assign patients with recurrent C. difficile infection to either antibiotic therapy or to duodenal infusion of donor feces. In order to estimate the sample size that would be needed, the investigators assumed that the feces infusion would be successful 90% of the time, and antibiotic therapy would be successful in 60% of cases. How many subjects will be needed in each group to ensure that the power of the study is 80% with a level of significance α = 0.05?
. The investigators planned to randomly assign patients with recurrent C. difficile infection to either antibiotic therapy or to duodenal infusion of donor feces. In order to estimate the sample size that would be needed, the investigators assumed that the feces infusion would be successful 90% of the time, and antibiotic therapy would be successful in 60% of cases. How many subjects will be needed in each group to ensure that the power of the study is 80% with a level of significance α = 0.05?