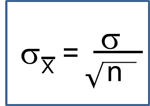Issues in Estimating Sample Size for Confidence Intervals Estimates
The module on confidence intervals provided methods for estimating confidence intervals for various parameters (e.g., μ , p, ( μ1 - μ2 ), μd , (p1-p2)). Confidence intervals for every parameter take the following general form:
Point Estimate + Margin of Error
In the module on confidence intervals we derived the formula for the confidence interval for μ as
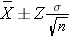
In practice we use the sample standard deviation to estimate the population standard deviation. Note that there is an alternative formula for estimating the mean of a continuous outcome in a single population, and it is used when the sample size is small (n<30). It involves a value from the t distribution, as opposed to one from the standard normal distribution, to reflect the desired level of confidence. When performing sample size computations, we use the large sample formula shown here. [Note: The resultant sample size might be small, and in the analysis stage, the appropriate confidence interval formula must be used.]
The point estimate for the population mean is the sample mean and the margin of error is
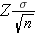
In planning studies, we want to determine the sample size needed to ensure that the margin of error is sufficiently small to be informative. For example, suppose we want to estimate the mean weight of female college students. We conduct a study and generate a 95% confidence interval as follows 125 + 40 pounds, or 85 to 165 pounds. The margin of error is so wide that the confidence interval is uninformative. To be informative, an investigator might want the margin of error to be no more than 5 or 10 pounds (meaning that the 95% confidence interval would have a width (lower limit to upper limit) of 10 or 20 pounds). In order to determine the sample size needed, the investigator must specify the desired margin of error. It is important to note that this is not a statistical issue, but a clinical or a practical one. For example, suppose we want to estimate the mean birth weight of infants born to mothers who smoke cigarettes during pregnancy. Birth weights in infants clearly have a much more restricted range than weights of female college students. Therefore, we would probably want to generate a confidence interval for the mean birth weight that has a margin of error not exceeding 1 or 2 pounds.
The margin of error in the one sample confidence interval for μ can be written as follows:
.
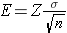Our goal is to determine the sample size, n, that ensures that the margin of error, "E," does not exceed a specified value. We can take the formula above and, with some algebra, solve for n:
First, multipy both sides of the equation by the square root of n. Then cancel out the square root of n from the numerator and denominator on the right side of the equation (since any number divided by itself is equal to 1). This leaves:
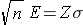
Now divide both sides by "E" and cancel out "E" from the numerator and denominator on the left side. This leaves:
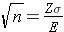
Finally, square both sides of the equation to get:
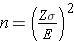
This formula generates the sample size, n, required to ensure that the margin of error, E, does not exceed a specified value. To solve for n, we must input "Z," "σ," and "E."
- Z is the value from the table of probabilities of the standard normal distribution for the desired confidence level (e.g., Z = 1.96 for 95% confidence)
- E is the margin of error that the investigator specifies as important from a clinical or practical standpoint.
- σ is the standard deviation of the outcome of interest.
Sometimes it is difficult to estimate σ. When we use the sample size formula above (or one of the other formulas that we will present in the sections that follow), we are planning a study to estimate the unknown mean of a particular outcome variable in a population. It is unlikely that we would know the standard deviation of that variable. In sample size computations, investigators often use a value for the standard deviation from a previous study or a study done in a different, but comparable, population. The sample size computation is not an application of statistical inference and therefore it is reasonable to use an appropriate estimate for the standard deviation. The estimate can be derived from a different study that was reported in the literature; some investigators perform a small pilot study to estimate the standard deviation. A pilot study usually involves a small number of participants (e.g., n=10) who are selected by convenience, as opposed to by random sampling. Data from the participants in the pilot study can be used to compute a sample standard deviation, which serves as a good estimate for σ in the sample size formula. Regardless of how the estimate of the variability of the outcome is derived, it should always be conservative (i.e., as large as is reasonable), so that the resultant sample size is not too small.
The formula 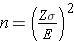produces the minimum sample size to ensure that the margin of error in a confidence interval will not exceed E. In planning studies, investigators should also consider attrition or loss to follow-up. The formula above gives the number of participants needed with complete data to ensure that the margin of error in the confidence interval does not exceed E. We will illustrate how attrition is addressed in planning studies through examples in the following sections.