Tests with Two Independent Samples, Dichotomous Outcome
Here we consider the situation where there are two independent comparison groups and the outcome of interest is dichotomous (e.g., success/failure). The goal of the analysis is to compare proportions of successes between the two groups. The relevant sample data are the sample sizes in each comparison group (n1 and n2) and the sample proportions (
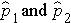 ) which are computed by taking the ratios of the numbers of successes to the sample sizes in each group, i.e.,
) which are computed by taking the ratios of the numbers of successes to the sample sizes in each group, i.e.,

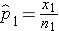 and
and 
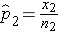
There are several approaches that can be used to test hypotheses concerning two independent proportions. Here we present one approach - the chi-square test of independence is an alternative, equivalent, and perhaps more popular approach to the same analysis. Hypothesis testing with the chi-square test is addressed in the third module in this series: BS704_HypothesisTesting-ChiSquare.
In tests of hypothesis comparing proportions between two independent groups, one test is performed and results can be interpreted to apply to a risk difference, relative risk or odds ratio. As a reminder, the risk difference is computed by taking the difference in proportions between comparison groups, the risk ratio is computed by taking the ratio of proportions, and the odds ratio is computed by taking the ratio of the odds of success in the comparison groups. Because the null values for the risk difference, the risk ratio and the odds ratio are different, the hypotheses in tests of hypothesis look slightly different depending on which measure is used. When performing tests of hypothesis for the risk difference, relative risk or odds ratio, the convention is to label the exposed or treated group 1 and the unexposed or control group 2.
For example, suppose a study is designed to assess whether there is a significant difference in proportions in two independent comparison groups. The test of interest is as follows:
H0: p1 = p2 versus H1: p1 ≠ p2.
The following are the hypothesis for testing for a difference in proportions using the risk difference, the risk ratio and the odds ratio. First, the hypotheses above are equivalent to the following:
- For the risk difference, H0: p1 - p2 = 0 versus H1: p1 - p2 ≠ 0 which are, by definition, equal to H0: RD = 0 versus H1: RD ≠ 0.
- If an investigator wants to focus on the risk ratio, the equivalent hypotheses are H0: RR = 1 versus H1: RR ≠ 1.
- If the investigator wants to focus on the odds ratio, the equivalent hypotheses are H0: OR = 1 versus H1: OR ≠ 1.
Suppose a test is performed to test H0: RD = 0 versus H1: RD ≠ 0 and the test rejects H0 at α=0.05. Based on this test we can conclude that there is significant evidence, α=0.05, of a difference in proportions, significant evidence that the risk difference is not zero, significant evidence that the risk ratio and odds ratio are not one. The risk difference is analogous to the difference in means when the outcome is continuous. Here the parameter of interest is the difference in proportions in the population, RD = p1-p2 and the null value for the risk difference is zero. In a test of hypothesis for the risk difference, the null hypothesis is always H0: RD = 0. This is equivalent to H0: RR = 1 and H0: OR = 1. In the research hypothesis, an investigator can hypothesize that the first proportion is larger than the second (H1: p 1 > p 2 , which is equivalent to H1: RD > 0, H1: RR > 1 and H1: OR > 1), that the first proportion is smaller than the second (H1: p 1 < p 2 , which is equivalent to H1: RD < 0, H1: RR < 1 and H1: OR < 1), or that the proportions are different (H1: p 1 ≠ p 2 , which is equivalent to H1: RD ≠ 0, H1: RR ≠ 1 and H1: OR ≠
1). The three different alternatives represent upper-, lower- and two-tailed tests, respectively.
The formula for the test of hypothesis for the difference in proportions is given below.
Test Statistics for Testing H0: p 1 = p

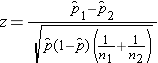
Where 
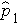 is the proportion of successes in sample 1,
is the proportion of successes in sample 1, 
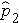 is the proportion of successes in sample 2, and
is the proportion of successes in sample 2, and 
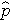 is the proportion of successes in the pooled sample.
is the proportion of successes in the pooled sample. 
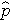 is computed by summing all of the successes and dividing by the total sample size, as follows:
is computed by summing all of the successes and dividing by the total sample size, as follows:

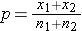
(this is similar to the pooled estimate of the standard deviation, Sp, used in two independent samples tests with a continuous outcome; just as Sp is in between s1 and s2, 
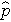 will be in between
will be in between 
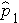 and
and 
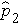 ).
).
The formula above is appropriate for large samples, defined as at least 5 successes (np>5) and at least 5 failures (n(1-p>5)) in each of the two samples. If there are fewer than 5 successes or failures in either comparison group, then alternative procedures, called exact methods must be used to estimate the difference in population proportions.
Example:
The following table summarizes data from n=3,799 participants who attended the fifth examination of the Offspring in the Framingham Heart Study. The outcome of interest is prevalent CVD and we want to test whether the prevalence of CVD is significantly higher in smokers as compared to non-smokers.
|
|
Free of CVD |
History of CVD |
Total |
|---|---|---|---|
|
Non-Smoker |
2,757 |
298 |
3,055 |
|
Current Smoker |
663 |
81 |
744 |
|
Total |
3,420 |
379 |
3,799 |
The prevalence of CVD (or proportion of participants with prevalent CVD) among non-smokers is 298/3,055 = 0.0975 and the prevalence of CVD among current smokers is 81/744 = 0.1089. Here smoking status defines the comparison groups and we will call the current smokers group 1 (exposed) and the non-smokers (unexposed) group 2. The test of hypothesis is conducted below using the five step approach.
- Step 1. Set up hypotheses and determine level of significance
H0: p1 = p2 H1: p1 ≠ p2 α=0.05
- Step 2. Select the appropriate test statistic.
We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group. In this example, we have more than enough successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group. The sample size is more than adequate so the following formula can be used:

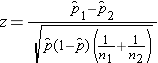
.
- Step 3. Set up decision rule.
Reject H0 if Z < -1.960 or if Z > 1.960.
- Step 4. Compute the test statistic.
We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

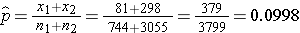
We now substitute to compute the test statistic.

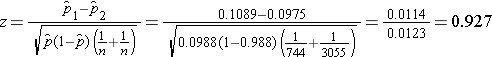
- Step 5. Conclusion.
We do not reject H0 because -1.960 < 0.927 < 1.960. We do not have statistically significant evidence at α=0.05 to show that there is a difference in prevalent CVD between smokers and non-smokers.
A 95% confidence interval for the difference in prevalent CVD (or risk difference) between smokers and non-smokers as 0.0114 + 0.0247, or between -0.0133 and 0.0361. Because the 95% confidence interval for the risk difference includes zero we again conclude that there is no statistically significant difference in prevalent CVD between smokers and non-smokers.
Smoking has been shown over and over to be a risk factor for cardiovascular disease. What might explain the fact that we did not observe a statistically significant difference using data from the Framingham Heart Study? HINT: Here we consider prevalent CVD, would the results have been different if we considered incident CVD?
Example:
A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.
|
Treatment Group |
n |
Number with Reduction of 3+ Points |
Proportion with Reduction of 3+ Points |
|---|---|---|---|
|
New Pain Reliever |
50 |
23 |
0.46 |
|
Standard Pain Reliever |
50 |
11 |
0.22 |
We now test whether there is a statistically significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using the five step approach.
- Step 1. Set up hypotheses and determine level of significance
H0: p1 = p2 H1: p1 ≠ p2 α=0.05
Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.
- Step 2. Select the appropriate test statistic.
We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group, i.e.,

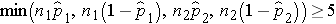
In this example, we have min(50(0.46), 50(1-0.46), 50(0.22), 50(1-0.22)) = min(23, 27, 11, 39) = 11. The sample size is adequate so the following formula can be used

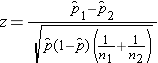
- Step 3. Set up decision rule.
Reject H0 if Z < -1.960 or if Z > 1.960.
- Step 4. Compute the test statistic.
We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

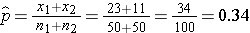
We now substitute to compute the test statistic.

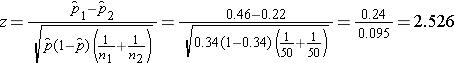
- Step 5. Conclusion.
We reject H0 because 2.526 > 1960. We have statistically significant evidence at a =0.05 to show that there is a difference in the proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever.
A 95% confidence interval for the difference in proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever is 0.24 + 0.18 or between 0.06 and 0.42. Because the 95% confidence interval does not include zero we concluded that there was a statistically significant difference in proportions which is consistent with the test of hypothesis result.
Again, the procedures discussed here apply to applications where there are two independent comparison groups and a dichotomous outcome. There are other applications in which it is of interest to compare a dichotomous outcome in matched or paired samples. For example, in a clinical trial we might wish to test the effectiveness of a new antibiotic eye drop for the treatment of bacterial conjunctivitis. Participants use the new antibiotic eye drop in one eye and a comparator (placebo or active control treatment) in the other. The success of the treatment (yes/no) is recorded for each participant for each eye. Because the two assessments (success or failure) are paired, we cannot use the procedures discussed here. The appropriate test is called McNemar's test (sometimes called McNemar's test for dependent proportions).
Vide0 - Hypothesis Testing With Two Independent Samples and a Dichotomous Outcome (2:55)
Link to transcript of the video