
Hypothesis Testing for Means & Proportions
Lisa Sullivan, PhD
Professor of Biostatistics
Boston University School of Public Health

This is the first of three modules that will addresses the second area of statistical inference, which is hypothesis testing, in which a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The process of hypothesis testing involves setting up two competing hypotheses, the null hypothesis and the alternate hypothesis. One selects a random sample (or multiple samples when there are more comparison groups), computes summary statistics and then assesses the likelihood that the sample data support the research or alternative hypothesis. Similar to estimation, the process of hypothesis testing is based on probability theory and the Central Limit Theorem.
This module will focus on hypothesis testing for means and proportions. The next two modules in this series will address analysis of variance and chi-squared tests.
After completing this module, the student will be able to:

The techniques for hypothesis testing depend on
In estimation we focused explicitly on techniques for one and two samples and discussed estimation for a specific parameter (e.g., the mean or proportion of a population), for differences (e.g., difference in means, the risk difference) and ratios (e.g., the relative risk and odds ratio). Here we will focus on procedures for one and two samples when the outcome is either continuous (and we focus on means) or dichotomous (and we focus on proportions).
The Centers for Disease Control (CDC) reported on trends in weight, height and body mass index from the 1960's through 2002.1 The general trend was that Americans were much heavier and slightly taller in 2002 as compared to 1960; both men and women gained approximately 24 pounds, on average, between 1960 and 2002. In 2002, the mean weight for men was reported at 191 pounds. Suppose that an investigator hypothesizes that weights are even higher in 2006 (i.e., that the trend continued over the subsequent 4 years). The research hypothesis is that the mean weight in men in 2006 is more than 191 pounds. The null hypothesis is that there is no change in weight, and therefore the mean weight is still 191 pounds in 2006.
|
Null Hypothesis |
H0: μ= 191 (no change) |
|
Research Hypothesis |
H1: μ> 191 (investigator's belief) |
In order to test the hypotheses, we select a random sample of American males in 2006 and measure their weights. Suppose we have resources available to recruit n=100 men into our sample. We weigh each participant and compute summary statistics on the sample data. Suppose in the sample we determine the following:
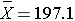
Do the sample data support the null or research hypothesis? The sample mean of 197.1 is numerically higher than 191. However, is this difference more than would be expected by chance? In hypothesis testing, we assume that the null hypothesis holds until proven otherwise. We therefore need to determine the likelihood of observing a sample mean of 197.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true or under the null hypothesis). We can compute this probability using the Central Limit Theorem. Specifically,
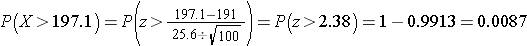
(Notice that we use the sample standard deviation in computing the Z score. This is generally an appropriate substitution as long as the sample size is large, n > 30. Thus, there is less than a 1% probability of observing a sample mean as large as 197.1 when the true population mean is 191. Do you think that the null hypothesis is likely true? Based on how unlikely it is to observe a sample mean of 197.1 under the null hypothesis (i.e., <1% probability), we might infer, from our data, that the null hypothesis is probably not true.
Suppose that the sample data had turned out differently. Suppose that we instead observed the following in 2006:
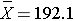
How likely it is to observe a sample mean of 192.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true)? We can again compute this probability using the Central Limit Theorem. Specifically,
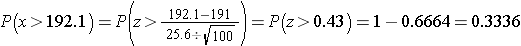
There is a 33.4% probability of observing a sample mean as large as 192.1 when the true population mean is 191. Do you think that the null hypothesis is likely true?
Neither of the sample means that we obtained allows us to know with certainty whether the null hypothesis is true or not. However, our computations suggest that, if the null hypothesis were true, the probability of observing a sample mean >197.1 is less than 1%. In contrast, if the null hypothesis were true, the probability of observing a sample mean >192.1 is about 33%. We can't know whether the null hypothesis is true, but the sample that provided a mean value of 197.1 provides much stronger evidence in favor of rejecting the null hypothesis, than the sample that provided a mean value of 192.1. Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it.
In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis. In hypothesis testing, we determine a threshold or cut-off point (called the critical value) to decide when to believe the null hypothesis and when to believe the research hypothesis. It is important to note that it is possible to observe any sample mean when the true population mean is true (in this example equal to 191), but some sample means are very unlikely. Based on the two samples above it would seem reasonable to believe the research hypothesis when x̄ = 197.1, but to believe the null hypothesis when x̄ =192.1. What we need is a threshold value such that if x̄ is above that threshold then we believe that H1 is true and if x̄ is below that threshold then we believe that H0 is true. The difficulty in determining a threshold for x̄ is that it depends on the scale of measurement. In this example, the threshold, sometimes called the critical value, might be 195 (i.e., if the sample mean is 195 or more then we believe that H1 is true and if the sample mean is less than 195 then we believe that H0 is true). Suppose we are interested in assessing an increase in blood pressure over time, the critical value will be different because blood pressures are measured in millimeters of mercury (mmHg) as opposed to in pounds. In the following we will explain how the critical value is determined and how we handle the issue of scale.
First, to address the issue of scale in determining the critical value, we convert our sample data (in particular the sample mean) into a Z score. We know from the module on probability that the center of the Z distribution is zero and extreme values are those that exceed 2 or fall below -2. Z scores above 2 and below -2 represent approximately 5% of all Z values. If the observed sample mean is close to the mean specified in H0 (here m =191), then Z will be close to zero. If the observed sample mean is much larger than the mean specified in H0, then Z will be large.
In hypothesis testing, we select a critical value from the Z distribution. This is done by first determining what is called the level of significance, denoted α ("alpha"). What we are doing here is drawing a line at extreme values. The level of significance is the probability that we reject the null hypothesis (in favor of the alternative) when it is actually true and is also called the Type I error rate.
α = Level of significance = P(Type I error) = P(Reject H0 | H0 is true).
Because α is a probability, it ranges between 0 and 1. The most commonly used value in the medical literature for α is 0.05, or 5%. Thus, if an investigator selects α=0.05, then they are allowing a 5% probability of incorrectly rejecting the null hypothesis in favor of the alternative when the null is in fact true. Depending on the circumstances, one might choose to use a level of significance of 1% or 10%. For example, if an investigator wanted to reject the null only if there were even stronger evidence than that ensured with α=0.05, they could choose a =0.01as their level of significance. The typical values for α are 0.01, 0.05 and 0.10, with α=0.05 the most commonly used value.
Suppose in our weight study we select α=0.05. We need to determine the value of Z that holds 5% of the values above it (see below).
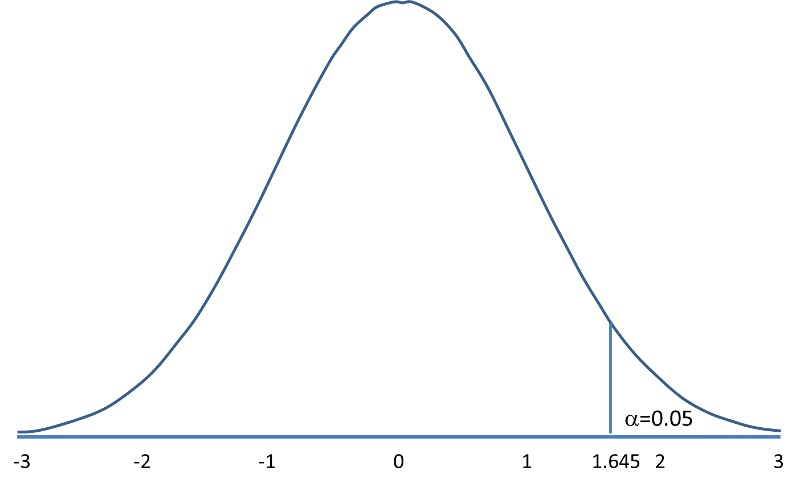
The critical value of Z for α =0.05 is Z = 1.645 (i.e., 5% of the distribution is above Z=1.645). With this value we can set up what is called our decision rule for the test. The rule is to reject H0 if the Z score is 1.645 or more.
With the first sample we have
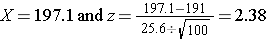
Because 2.38 > 1.645, we reject the null hypothesis. (The same conclusion can be drawn by comparing the 0.0087 probability of observing a sample mean as extreme as 197.1 to the level of significance of 0.05. If the observed probability is smaller than the level of significance we reject H0). Because the Z score exceeds the critical value, we conclude that the mean weight for men in 2006 is more than 191 pounds, the value reported in 2002. If we observed the second sample (i.e., sample mean =192.1), we would not be able to reject the null hypothesis because the Z score is 0.43 which is not in the rejection region (i.e., the region in the tail end of the curve above 1.645). With the second sample we do not have sufficient evidence (because we set our level of significance at 5%) to conclude that weights have increased. Again, the same conclusion can be reached by comparing probabilities. The probability of observing a sample mean as extreme as 192.1 is 33.4% which is not below our 5% level of significance.
The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.
H0: Null hypothesis (no change, no difference);
H1: Research hypothesis (investigator's belief); α =0.05
|
Upper-tailed, Lower-tailed, Two-tailed Tests The research or alternative hypothesis can take one of three forms. An investigator might believe that the parameter has increased, decreased or changed. For example, an investigator might hypothesize:
The exact form of the research hypothesis depends on the investigator's belief about the parameter of interest and whether it has possibly increased, decreased or is different from the null value. The research hypothesis is set up by the investigator before any data are collected.
|
The test statistic is a single number that summarizes the sample information. An example of a test statistic is the Z statistic computed as follows:
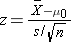
When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.
The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.
The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.
|
Rejection Region for Upper-Tailed Z Test (H1: μ > μ0 ) with α=0.05 The decision rule is: Reject H0 if Z > 1.645. |
|
||||||||||||||||||
|
Rejection Region for Lower-Tailed Z Test (H1: μ < μ0 ) with α =0.05 The decision rule is: Reject H0 if Z < 1.645. |
|
||||||||||||||||||
|
Rejection Region for Two-Tailed Z Test (H1: μ ≠ μ 0 ) with α =0.05 The decision rule is: Reject H0 if Z < -1.960 or if Z > 1.960. |
|
||||||||||||||||||
The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."
Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."
Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.
The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).
If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H0.
Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H0.
|
Things to Remember When Interpreting P Values
|
We now use the five-step procedure to test the research hypothesis that the mean weight in men in 2006 is more than 191 pounds. We will assume the sample data are as follows: n=100, 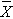 =197.1 and s=25.6.
=197.1 and s=25.6.
H0: μ = 191 H1: μ > 191 α =0.05
The research hypothesis is that weights have increased, and therefore an upper tailed test is used.
Because the sample size is large (n>30) the appropriate test statistic is
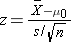
In this example, we are performing an upper tailed test (H1: μ> 191), with a Z test statistic and selected α =0.05. Reject H0 if Z > 1.645.
We now substitute the sample data into the formula for the test statistic identified in Step 2.
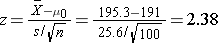
We reject H0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H0. In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H0. In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.
In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).
Table - Conclusions in Test of Hypothesis
|
|
Do Not Reject H0 |
Reject H0 |
|---|---|---|
|
H0 is True |
Correct Decision |
Type I Error |
|
H0 is False |
Type II Error |
Correct Decision |
In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H0, then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H0 that the research hypothesis is true (as it is the more likely scenario when we reject H0).
When we run a test of hypothesis and decide not to reject H0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H0 | H0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H0, it may be very likely that we are committing a Type II error (i.e., failing to reject H0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H0, we conclude that we do not have significant evidence to show that H1 is true. We do not conclude that H0 is true.

The most common reason for a Type II error is a small sample size.
Hypothesis testing applications with a continuous outcome variable in a single population are performed according to the five-step procedure outlined above. A key component is setting up the null and research hypotheses. The objective is to compare the mean in a single population to known mean (μ0). The known value is generally derived from another study or report, for example a study in a similar, but not identical, population or a study performed some years ago. The latter is called a historical control. It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.
In one sample tests for a continuous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data - including the sample size (n), the sample mean ( 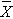 ) and the sample standard deviation (s). We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formulas for test statistics depend on the sample size and are given below.
) and the sample standard deviation (s). We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formulas for test statistics depend on the sample size and are given below.
Test Statistics for Testing H0: μ= μ0
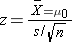
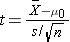 where df=n-1
where df=n-1
Note that statistical computing packages will use the t statistic exclusively and make the necessary adjustments for comparing the test statistic to appropriate values from probability tables to produce a p-value.
Example:
The National Center for Health Statistics (NCHS) published a report in 2005 entitled Health, United States, containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races. The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured. The sample data are summarized as follows: n=100, x̄
=$3,190 and s=$890. Is there statistical evidence of a reduction in expenditures on health care and prescription drugs in 2005? Is the sample mean of $3,190 evidence of a true reduction in the mean or is it within chance fluctuation? We will run the test using the five-step approach.
H0: μ = 3,302 H1: μ < 3,302 α =0.05
The research hypothesis is that expenditures have decreased, and therefore a lower-tailed test is used.
Because the sample size is large (n> 30) the appropriate test statistic is
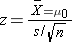
This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H0 if Z < -1.645.
We now substitute the sample data into the formula for the test statistic identified in Step 2.
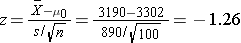
We do not reject H0 because -1.26 > -1.645. We do not have statistically significant evidence at α=0.05 to show that the mean expenditures on health care and prescription drugs are lower in 2005 than the mean of $3,302 reported in 2002.
Recall that when we fail to reject H0 in a test of hypothesis that either the null hypothesis is true (here the mean expenditures in 2005 are the same as those in 2002 and equal to $3,302) or we committed a Type II error (i.e., we failed to reject H0 when in fact it is false). In summarizing this test, we conclude that we do not have sufficient evidence to reject H0. We do not conclude that H0 is true, because there may be a moderate to high probability that we committed a Type II error. It is possible that the sample size is not large enough to detect a difference in mean expenditures.
Example:
The NCHS reported that the mean total cholesterol level in 2002 for all adults was 203. Total cholesterol levels in participants who attended the seventh examination of the Offspring in the Framingham Heart Study are summarized as follows: n=3,310, x̄ =200.3, and s=36.8. Is there statistical evidence of a difference in mean cholesterol levels in the Framingham Offspring?
Here we want to assess whether the sample mean of 200.3 in the Framingham sample is statistically significantly different from 203 (i.e., beyond what we would expect by chance). We will run the test using the five-step approach.
H0: μ= 203 H1: μ≠ 203 α=0.05
The research hypothesis is that cholesterol levels are different in the Framingham Offspring, and therefore a two-tailed test is used.
Because the sample size is large (n>30) the appropriate test statistic is
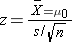
This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H0 if Z < -1.960 or is Z > 1.960.
We now substitute the sample data into the formula for the test statistic identified in Step 2.
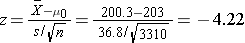
We reject H0 because -4.22 ≤ -1. .960. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level in the Framingham Offspring is different from the national average of 203 reported in 2002. Because we reject H0, we also approximate a p-value. Using the two-sided significance levels, p < 0.0001.
This example raises an important concept of statistical versus clinical or practical significance. From a statistical standpoint, the total cholesterol levels in the Framingham sample are highly statistically significantly different from the national average with p < 0.0001 (i.e., there is less than a 0.01% chance that we are incorrectly rejecting the null hypothesis). However, the sample mean in the Framingham Offspring study is 200.3, less than 3 units different from the national mean of 203. The reason that the data are so highly statistically significant is due to the very large sample size. It is always important to assess both statistical and clinical significance of data. This is particularly relevant when the sample size is large. Is a 3 unit difference in total cholesterol a meaningful difference?
Example:
Consider again the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. Suppose a new drug is proposed to lower total cholesterol. A study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients are enrolled in the study and asked to take the new drug for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows: n=15, x̄ =195.9 and s=28.7. Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new drug for 6 weeks? We will run the test using the five-step approach.
H0: μ= 203 H1: μ< 203 α=0.05
Because the sample size is small (n<30) the appropriate test statistic is
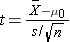 .
.
This is a lower tailed test, using a t statistic and a 5% level of significance. In order to determine the critical value of t, we need degrees of freedom, df, defined as df=n-1. In this example df=15-1=14. The critical value for a lower tailed test with df=14 and a =0.05 is -2.145 and the decision rule is as follows: Reject H0 if t < -2.145.
We now substitute the sample data into the formula for the test statistic identified in Step 2.
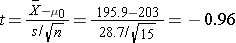
We do not reject H0 because -0.96 > -2.145. We do not have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower than the national mean in patients taking the new drug for 6 weeks. Again, because we failed to reject the null hypothesis we make a weaker concluding statement allowing for the possibility that we may have committed a Type II error (i.e., failed to reject H0 when in fact the drug is efficacious).

This example raises an important issue in terms of study design. In this example we assume in the null hypothesis that the mean cholesterol level is 203. This is taken to be the mean cholesterol level in patients without treatment. Is this an appropriate comparator? Alternative and potentially more efficient study designs to evaluate the effect of the new drug could involve two treatment groups, where one group receives the new drug and the other does not, or we could measure each patient's baseline or pre-treatment cholesterol level and then assess changes from baseline to 6 weeks post-treatment. These designs are also discussed here.
Video - Comparing a Sample Mean to Known Population Mean (8:20)
Link to transcript of the video
Hypothesis testing applications with a dichotomous outcome variable in a single population are also performed according to the five-step procedure. Similar to tests for means, a key component is setting up the null and research hypotheses. The objective is to compare the proportion of successes in a single population to a known proportion (p0). That known proportion is generally derived from another study or report and is sometimes called a historical control. It is important in setting up the hypotheses in a one sample test that the proportion specified in the null hypothesis is a fair and reasonable comparator.
In one sample tests for a dichotomous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the sample proportion which is computed by taking the ratio of the number of successes to the sample size,
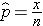
We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formula for the test statistic is given below.
Test Statistic for Testing H0: p = p 0
if min(np0 , n(1-p0))> 5
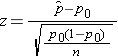
The formula above is appropriate for large samples, defined when the smaller of np0 and n(1-p0) is at least 5. This is similar, but not identical, to the condition required for appropriate use of the confidence interval formula for a population proportion, i.e.,
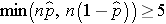
Here we use the proportion specified in the null hypothesis as the true proportion of successes rather than the sample proportion. If we fail to satisfy the condition, then alternative procedures, called exact methods must be used to test the hypothesis about the population proportion.
.
Example:
The NCHS report indicated that in 2002 the prevalence of cigarette smoking among American adults was 21.1%. Data on prevalent smoking in n=3,536 participants who attended the seventh examination of the Offspring in the Framingham Heart Study indicated that 482/3,536 = 13.6% of the respondents were currently smoking at the time of the exam. Suppose we want to assess whether the prevalence of smoking is lower in the Framingham Offspring sample given the focus on cardiovascular health in that community. Is there evidence of a statistically lower prevalence of smoking in the Framingham Offspring study as compared to the prevalence among all Americans?
H0: p = 0.211 H1: p < 0.211 α=0.05
We must first check that the sample size is adequate. Specifically, we need to check min(np0, n(1-p0)) = min( 3,536(0.211), 3,536(1-0.211))=min(746, 2790)=746. The sample size is more than adequate so the following formula can be used:
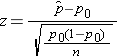 .
.
This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H0 if Z < -1.645.
We now substitute the sample data into the formula for the test statistic identified in Step 2.
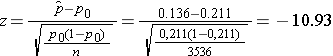
We reject H0 because -10.93 < -1.645. We have statistically significant evidence at α=0.05 to show that the prevalence of smoking in the Framingham Offspring is lower than the prevalence nationally (21.1%). Here, p < 0.0001.

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?
Calculate this on your own before checking the answer.
Answer
Video - Hypothesis Test for One Sample and a Dichotomous Outcome (3:55)
Link to transcript of the video
There are many applications where it is of interest to compare two independent groups with respect to their mean scores on a continuous outcome. Here we compare means between groups, but rather than generating an estimate of the difference, we will test whether the observed difference (increase, decrease or difference) is statistically significant or not. Remember, that hypothesis testing gives an assessment of statistical significance, whereas estimation gives an estimate of effect and both are important.
Here we discuss the comparison of means when the two comparison groups are independent or physically separate. The two groups might be determined by a particular attribute (e.g., sex, diagnosis of cardiovascular disease) or might be set up by the investigator (e.g., participants assigned to receive an experimental treatment or placebo). The first step in the analysis involves computing descriptive statistics on each of the two samples. Specifically, we compute the sample size, mean and standard deviation in each sample and we denote these summary statistics as follows:
for sample 1:
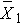
for sample 2:
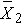
The designation of sample 1 and sample 2 is arbitrary. In a clinical trial setting the convention is to call the treatment group 1 and the control group 2. However, when comparing men and women, for example, either group can be 1 or 2.
In the two independent samples application with a continuous outcome, the parameter of interest in the test of hypothesis is the difference in population means, μ1-μ2. The null hypothesis is always that there is no difference between groups with respect to means, i.e.,
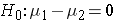
The null hypothesis can also be written as follows: H0: μ1 = μ2. In the research hypothesis, an investigator can hypothesize that the first mean is larger than the second (H1: μ1 > μ2 ), that the first mean is smaller than the second (H1: μ1 < μ2 ), or that the means are different (H1: μ1 ≠ μ2 ). The three different alternatives represent upper-, lower-, and two-tailed tests, respectively. The following test statistics are used to test these hypotheses.
Test Statistics for Testing H0: μ1 = μ2
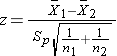
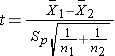 where df =n1+n2-2.
where df =n1+n2-2.
NOTE: The formulas above assume equal variability in the two populations (i.e., the population variances are equal, or s12 = s22). This means that the outcome is equally variable in each of the comparison populations. For analysis, we have samples from each of the comparison populations. If the sample variances are similar, then the assumption about variability in the populations is probably reasonable. As a guideline, if the ratio of the sample variances, s12/s22 is between 0.5 and 2 (i.e., if one variance is no more than double the other), then the formulas above are appropriate. If the ratio of the sample variances is greater than 2 or less than 0.5 then alternative formulas must be used to account for the heterogeneity in variances.
The test statistics include Sp, which is the pooled estimate of the common standard deviation (again assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples as follows:
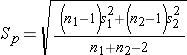
Because we are assuming equal variances between groups, we pool the information on variability (sample variances) to generate an estimate of the variability in the population. Note: Because Sp is a weighted average of the standard deviations in the sample, Sp will always be in between s1 and s2.)
Example:
Data measured on n=3,539 participants who attended the seventh examination of the Offspring in the Framingham Heart Study are shown below.
|
|
Men |
Women |
||||
|
Characteristic |
n |
|
S |
n |
|
s |
|
Systolic Blood Pressure |
1,623 |
128.2 |
17.5 |
1,911 |
126.5 |
20.1 |
|
Diastolic Blood Pressure |
1,622 |
75.6 |
9.8 |
1,910 |
72.6 |
9.7 |
|
Total Serum Cholesterol |
1,544 |
192.4 |
35.2 |
1,766 |
207.1 |
36.7 |
|
Weight |
1,612 |
194.0 |
33.8 |
1,894 |
157.7 |
34.6 |
|
Height |
1,545 |
68.9 |
2.7 |
1,781 |
63.4 |
2.5 |
|
Body Mass Index |
1,545 |
28.8 |
4.6 |
1,781 |
27.6 |
5.9 |
Suppose we now wish to assess whether there is a statistically significant difference in mean systolic blood pressures between men and women using a 5% level of significance.
H0: μ1 = μ2
H1: μ1 ≠ μ2 α=0.05
Because both samples are large (> 30), we can use the Z test statistic as opposed to t. Note that statistical computing packages use t throughout. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The guideline suggests investigating the ratio of the sample variances, s12/s22. Suppose we call the men group 1 and the women group 2. Again, this is arbitrary; it only needs to be noted when interpreting the results. The ratio of the sample variances is 17.52/20.12 = 0.76, which falls between 0.5 and 2 suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is
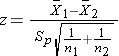 .
.
This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H0 if Z < -1.960 or is Z > 1.960.
We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.
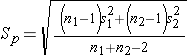
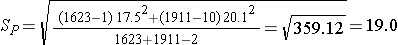
Notice that the pooled estimate of the common standard deviation, Sp, falls in between the standard deviations in the comparison groups (i.e., 17.5 and 20.1). Sp is slightly closer in value to the standard deviation in the women (20.1) as there were slightly more women in the sample. Recall, Sp is a weight average of the standard deviations in the comparison groups, weighted by the respective sample sizes.
Now the test statistic:
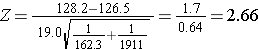
We reject H0 because 2.66 > 1.960. We have statistically significant evidence at α=0.05 to show that there is a difference in mean systolic blood pressures between men and women. The p-value is p < 0.010.
Here again we find that there is a statistically significant difference in mean systolic blood pressures between men and women at p < 0.010. Notice that there is a very small difference in the sample means (128.2-126.5 = 1.7 units), but this difference is beyond what would be expected by chance. Is this a clinically meaningful difference? The large sample size in this example is driving the statistical significance. A 95% confidence interval for the difference in mean systolic blood pressures is: 1.7 + 1.26 or (0.44, 2.96). The confidence interval provides an assessment of the magnitude of the difference between means whereas the test of hypothesis and p-value provide an assessment of the statistical significance of the difference.
Above we performed a study to evaluate a new drug designed to lower total cholesterol. The study involved one sample of patients, each patient took the new drug for 6 weeks and had their cholesterol measured. As a means of evaluating the efficacy of the new drug, the mean total cholesterol following 6 weeks of treatment was compared to the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. At the end of the example, we discussed the appropriateness of the fixed comparator as well as an alternative study design to evaluate the effect of the new drug involving two treatment groups, where one group receives the new drug and the other does not. Here, we revisit the example with a concurrent or parallel control group, which is very typical in randomized controlled trials or clinical trials (refer to the EP713 module on Clinical Trials).
Example:
A new drug is proposed to lower total cholesterol. A randomized controlled trial is designed to evaluate the efficacy of the medication in lowering cholesterol. Thirty participants are enrolled in the trial and are randomly assigned to receive either the new drug or a placebo. The participants do not know which treatment they are assigned. Each participant is asked to take the assigned treatment for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows.
|
Treatment |
Sample Size |
Mean |
Standard Deviation |
|---|---|---|---|
|
New Drug |
15 |
195.9 |
28.7 |
|
Placebo |
15 |
227.4 |
30.3 |
Is there statistical evidence of a reduction in mean total cholesterol in patients taking the new drug for 6 weeks as compared to participants taking placebo? We will run the test using the five-step approach.
H0: μ1 = μ2 H1: μ1 < μ2 α=0.05
Because both samples are small (< 30), we use the t test statistic. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The ratio of the sample variances, s12/s22 =28.72/30.32 = 0.90, which falls between 0.5 and 2, suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is:
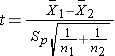 .
.
This is a lower-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table (in More Resources to the right). In order to determine the critical value of t we need degrees of freedom, df, defined as df=n1+n2-2 = 15+15-2=28. The critical value for a lower tailed test with df=28 and α=0.05 is -1.701 and the decision rule is: Reject H0 if t < -1.701.
We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.
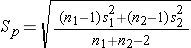
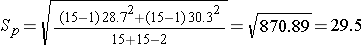
Now the test statistic,
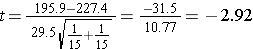
We reject H0 because -2.92 < -1.701. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower in patients taking the new drug for 6 weeks as compared to patients taking placebo, p < 0.005.
The clinical trial in this example finds a statistically significant reduction in total cholesterol, whereas in the previous example where we had a historical control (as opposed to a parallel control group) we did not demonstrate efficacy of the new drug. Notice that the mean total cholesterol level in patients taking placebo is 217.4 which is very different from the mean cholesterol reported among all Americans in 2002 of 203 and used as the comparator in the prior example. The historical control value may not have been the most appropriate comparator as cholesterol levels have been increasing over time. In the next section, we present another design that can be used to assess the efficacy of the new drug.
Video - Comparison of Two Independent Samples With a Continuous Outcome (8:02)
Link to transcript of the video
In the previous section we compared two groups with respect to their mean scores on a continuous outcome. An alternative study design is to compare matched or paired samples. The two comparison groups are said to be dependent, and the data can arise from a single sample of participants where each participant is measured twice (possibly before and after an intervention) or from two samples that are matched on specific characteristics (e.g., siblings). When the samples are dependent, we focus on difference scores in each participant or between members of a pair and the test of hypothesis is based on the mean difference, μd. The null hypothesis again reflects "no difference" and is stated as H0: μd =0 . Note that there are some instances where it is of interest to test whether there is a difference of a particular magnitude (e.g., μd =5) but in most instances the null hypothesis reflects no difference (i.e., μd=0).
The appropriate formula for the test of hypothesis depends on the sample size. The formulas are shown below and are identical to those we presented for estimating the mean of a single sample presented (e.g., when comparing against an external or historical control), except here we focus on difference scores.
Test Statistics for Testing H0: μd =0
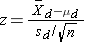
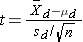 where df =n-1
where df =n-1
Example:
A new drug is proposed to lower total cholesterol and a study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients agree to participate in the study and each is asked to take the new drug for 6 weeks. However, before starting the treatment, each patient's total cholesterol level is measured. The initial measurement is a pre-treatment or baseline value. After taking the drug for 6 weeks, each patient's total cholesterol level is measured again and the data are shown below. The rightmost column contains difference scores for each patient, computed by subtracting the 6 week cholesterol level from the baseline level. The differences represent the reduction in total cholesterol over 4 weeks. (The differences could have been computed by subtracting the baseline total cholesterol level from the level measured at 6 weeks. The way in which the differences are computed does not affect the outcome of the analysis only the interpretation.)
|
Subject Identification Number |
Baseline |
6 Weeks |
Difference |
|---|---|---|---|
|
1 |
215 |
205 |
10 |
|
2 |
190 |
156 |
34 |
|
3 |
230 |
190 |
40 |
|
4 |
220 |
180 |
40 |
|
5 |
214 |
201 |
13 |
|
6 |
240 |
227 |
13 |
|
7 |
210 |
197 |
13 |
|
8 |
193 |
173 |
20 |
|
9 |
210 |
204 |
6 |
|
10 |
230 |
217 |
13 |
|
11 |
180 |
142 |
38 |
|
12 |
260 |
262 |
-2 |
|
13 |
210 |
207 |
3 |
|
14 |
190 |
184 |
6 |
|
15 |
200 |
193 |
7 |
Because the differences are computed by subtracting the cholesterols measured at 6 weeks from the baseline values, positive differences indicate reductions and negative differences indicate increases (e.g., participant 12 increases by 2 units over 6 weeks). The goal here is to test whether there is a statistically significant reduction in cholesterol. Because of the way in which we computed the differences, we want to look for an increase in the mean difference (i.e., a positive reduction). In order to conduct the test, we need to summarize the differences. In this sample, we have
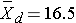
The calculations are shown below.
|
Subject Identification Number |
Difference |
Difference2 |
|---|---|---|
|
1 |
10 |
100 |
|
2 |
34 |
1156 |
|
3 |
40 |
1600 |
|
4 |
40 |
1600 |
|
5 |
13 |
169 |
|
6 |
13 |
169 |
|
7 |
13 |
169 |
|
8 |
20 |
400 |
|
9 |
6 |
36 |
|
10 |
13 |
169 |
|
11 |
38 |
1444 |
|
12 |
-2 |
4 |
|
13 |
3 |
9 |
|
14 |
6 |
36 |
|
15 |
7 |
49 |
| Totals |
254 |
7110 |
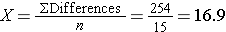
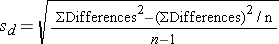
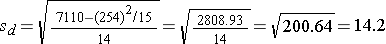
Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new medication for 6 weeks? We will run the test using the five-step approach.
H0: μd = 0 H1: μd > 0 α=0.05
NOTE: If we had computed differences by subtracting the baseline level from the level measured at 6 weeks then negative differences would have reflected reductions and the research hypothesis would have been H1: μd < 0.
Because the sample size is small (n<30) the appropriate test statistic is
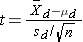 .
.
This is an upper-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table at the right, with df=15-1=14. The critical value for an upper-tailed test with df=14 and α=0.05 is 2.145 and the decision rule is Reject H0 if t > 2.145.
We now substitute the sample data into the formula for the test statistic identified in Step 2.
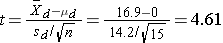
We reject H0 because 4.61 > 2.145. We have statistically significant evidence at α=0.05 to show that there is a reduction in cholesterol levels over 6 weeks.
Here we illustrate the use of a matched design to test the efficacy of a new drug to lower total cholesterol. We also considered a parallel design (randomized clinical trial) and a study using a historical comparator. It is extremely important to design studies that are best suited to detect a meaningful difference when one exists. There are often several alternatives and investigators work with biostatisticians to determine the best design for each application. It is worth noting that the matched design used here can be problematic in that observed differences may only reflect a "placebo" effect. All participants took the assigned medication, but is the observed reduction attributable to the medication or a result of these participation in a study.
Video - Hypothesis Testing With a Matched Sample and a Continuous Outcome (3:11)
Link to transcript of the video
Here we consider the situation where there are two independent comparison groups and the outcome of interest is dichotomous (e.g., success/failure). The goal of the analysis is to compare proportions of successes between the two groups. The relevant sample data are the sample sizes in each comparison group (n1 and n2) and the sample proportions (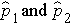 ) which are computed by taking the ratios of the numbers of successes to the sample sizes in each group, i.e.,
) which are computed by taking the ratios of the numbers of successes to the sample sizes in each group, i.e.,
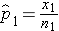 and
and 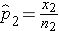
There are several approaches that can be used to test hypotheses concerning two independent proportions. Here we present one approach - the chi-square test of independence is an alternative, equivalent, and perhaps more popular approach to the same analysis. Hypothesis testing with the chi-square test is addressed in the third module in this series: BS704_HypothesisTesting-ChiSquare.
In tests of hypothesis comparing proportions between two independent groups, one test is performed and results can be interpreted to apply to a risk difference, relative risk or odds ratio. As a reminder, the risk difference is computed by taking the difference in proportions between comparison groups, the risk ratio is computed by taking the ratio of proportions, and the odds ratio is computed by taking the ratio of the odds of success in the comparison groups. Because the null values for the risk difference, the risk ratio and the odds ratio are different, the hypotheses in tests of hypothesis look slightly different depending on which measure is used. When performing tests of hypothesis for the risk difference, relative risk or odds ratio, the convention is to label the exposed or treated group 1 and the unexposed or control group 2.
For example, suppose a study is designed to assess whether there is a significant difference in proportions in two independent comparison groups. The test of interest is as follows:
H0: p1 = p2 versus H1: p1 ≠ p2.
The following are the hypothesis for testing for a difference in proportions using the risk difference, the risk ratio and the odds ratio. First, the hypotheses above are equivalent to the following:
Suppose a test is performed to test H0: RD = 0 versus H1: RD ≠ 0 and the test rejects H0 at α=0.05. Based on this test we can conclude that there is significant evidence, α=0.05, of a difference in proportions, significant evidence that the risk difference is not zero, significant evidence that the risk ratio and odds ratio are not one. The risk difference is analogous to the difference in means when the outcome is continuous. Here the parameter of interest is the difference in proportions in the population, RD = p1-p2 and the null value for the risk difference is zero. In a test of hypothesis for the risk difference, the null hypothesis is always H0: RD = 0. This is equivalent to H0: RR = 1 and H0: OR = 1. In the research hypothesis, an investigator can hypothesize that the first proportion is larger than the second (H1: p 1 > p 2 , which is equivalent to H1: RD > 0, H1: RR > 1 and H1: OR > 1), that the first proportion is smaller than the second (H1: p 1 < p 2 , which is equivalent to H1: RD < 0, H1: RR < 1 and H1: OR < 1), or that the proportions are different (H1: p 1 ≠ p 2 , which is equivalent to H1: RD ≠ 0, H1: RR ≠ 1 and H1: OR ≠
1). The three different alternatives represent upper-, lower- and two-tailed tests, respectively.
The formula for the test of hypothesis for the difference in proportions is given below.
Test Statistics for Testing H0: p 1 = p
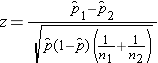
Where 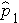 is the proportion of successes in sample 1,
is the proportion of successes in sample 1, 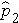 is the proportion of successes in sample 2, and
is the proportion of successes in sample 2, and 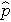 is the proportion of successes in the pooled sample.
is the proportion of successes in the pooled sample. 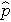 is computed by summing all of the successes and dividing by the total sample size, as follows:
is computed by summing all of the successes and dividing by the total sample size, as follows:
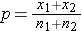
(this is similar to the pooled estimate of the standard deviation, Sp, used in two independent samples tests with a continuous outcome; just as Sp is in between s1 and s2, 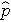 will be in between
will be in between 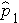 and
and 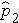 ).
).
The formula above is appropriate for large samples, defined as at least 5 successes (np>5) and at least 5 failures (n(1-p>5)) in each of the two samples. If there are fewer than 5 successes or failures in either comparison group, then alternative procedures, called exact methods must be used to estimate the difference in population proportions.
Example:
The following table summarizes data from n=3,799 participants who attended the fifth examination of the Offspring in the Framingham Heart Study. The outcome of interest is prevalent CVD and we want to test whether the prevalence of CVD is significantly higher in smokers as compared to non-smokers.
|
|
Free of CVD |
History of CVD |
Total |
|---|---|---|---|
|
Non-Smoker |
2,757 |
298 |
3,055 |
|
Current Smoker |
663 |
81 |
744 |
|
Total |
3,420 |
379 |
3,799 |
The prevalence of CVD (or proportion of participants with prevalent CVD) among non-smokers is 298/3,055 = 0.0975 and the prevalence of CVD among current smokers is 81/744 = 0.1089. Here smoking status defines the comparison groups and we will call the current smokers group 1 (exposed) and the non-smokers (unexposed) group 2. The test of hypothesis is conducted below using the five step approach.
H0: p1 = p2 H1: p1 ≠ p2 α=0.05
We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group. In this example, we have more than enough successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group. The sample size is more than adequate so the following formula can be used:
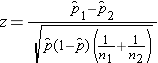
.
Reject H0 if Z < -1.960 or if Z > 1.960.
We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:
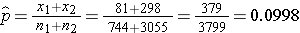
We now substitute to compute the test statistic.
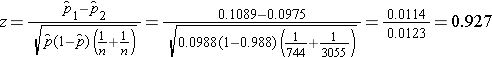
We do not reject H0 because -1.960 < 0.927 < 1.960. We do not have statistically significant evidence at α=0.05 to show that there is a difference in prevalent CVD between smokers and non-smokers.
A 95% confidence interval for the difference in prevalent CVD (or risk difference) between smokers and non-smokers as 0.0114 + 0.0247, or between -0.0133 and 0.0361. Because the 95% confidence interval for the risk difference includes zero we again conclude that there is no statistically significant difference in prevalent CVD between smokers and non-smokers.
Smoking has been shown over and over to be a risk factor for cardiovascular disease. What might explain the fact that we did not observe a statistically significant difference using data from the Framingham Heart Study? HINT: Here we consider prevalent CVD, would the results have been different if we considered incident CVD?
Example:
A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.
|
Treatment Group |
n |
Number with Reduction of 3+ Points |
Proportion with Reduction of 3+ Points |
|---|---|---|---|
|
New Pain Reliever |
50 |
23 |
0.46 |
|
Standard Pain Reliever |
50 |
11 |
0.22 |
We now test whether there is a statistically significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using the five step approach.
H0: p1 = p2 H1: p1 ≠ p2 α=0.05
Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.
We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group, i.e.,
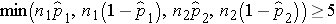
In this example, we have min(50(0.46), 50(1-0.46), 50(0.22), 50(1-0.22)) = min(23, 27, 11, 39) = 11. The sample size is adequate so the following formula can be used
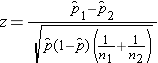
Reject H0 if Z < -1.960 or if Z > 1.960.
We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:
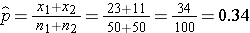
We now substitute to compute the test statistic.
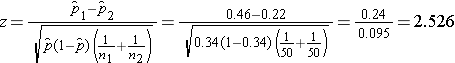
We reject H0 because 2.526 > 1960. We have statistically significant evidence at a =0.05 to show that there is a difference in the proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever.
A 95% confidence interval for the difference in proportions of patients on the new pain reliever reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) as compared to patients on the standard pain reliever is 0.24 + 0.18 or between 0.06 and 0.42. Because the 95% confidence interval does not include zero we concluded that there was a statistically significant difference in proportions which is consistent with the test of hypothesis result.
Again, the procedures discussed here apply to applications where there are two independent comparison groups and a dichotomous outcome. There are other applications in which it is of interest to compare a dichotomous outcome in matched or paired samples. For example, in a clinical trial we might wish to test the effectiveness of a new antibiotic eye drop for the treatment of bacterial conjunctivitis. Participants use the new antibiotic eye drop in one eye and a comparator (placebo or active control treatment) in the other. The success of the treatment (yes/no) is recorded for each participant for each eye. Because the two assessments (success or failure) are paired, we cannot use the procedures discussed here. The appropriate test is called McNemar's test (sometimes called McNemar's test for dependent proportions).
Vide0 - Hypothesis Testing With Two Independent Samples and a Dichotomous Outcome (2:55)
Link to transcript of the video
Here we presented hypothesis testing techniques for means and proportions in one and two sample situations. Tests of hypothesis involve several steps, including specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. There are many details to consider in hypothesis testing. The first is to determine the appropriate test. We discussed Z and t tests here for different applications. The appropriate test depends on the distribution of the outcome variable (continuous or dichotomous), the number of comparison groups (one, two) and whether the comparison groups are independent or dependent. The following table summarizes the different tests of hypothesis discussed here.
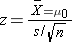
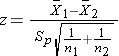
and 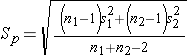
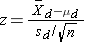
and
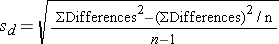
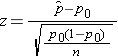
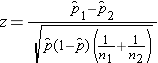
Once the type of test is determined, the details of the test must be specified. Specifically, the null and alternative hypotheses must be clearly stated. The null hypothesis always reflects the "no change" or "no difference" situation. The alternative or research hypothesis reflects the investigator's belief. The investigator might hypothesize that a parameter (e.g., a mean, proportion, difference in means or proportions) will increase, will decrease or will be different under specific conditions (sometimes the conditions are different experimental conditions and other times the conditions are simply different groups of participants). Once the hypotheses are specified, data are collected and summarized. The appropriate test is then conducted according to the five step approach. If the test leads to rejection of the null hypothesis, an approximate p-value is computed to summarize the significance of the findings. When tests of hypothesis are conducted using statistical computing packages, exact p-values are computed. Because the statistical tables in this textbook are limited, we can only approximate p-values. If the test fails to reject the null hypothesis, then a weaker concluding statement is made for the following reason.
In hypothesis testing, there are two types of errors that can be committed. A Type I error occurs when a test incorrectly rejects the null hypothesis. This is referred to as a false positive result, and the probability that this occurs is equal to the level of significance, α. The investigator chooses the level of significance in Step 1, and purposely chooses a small value such as α=0.05 to control the probability of committing a Type I error. A Type II error occurs when a test fails to reject the null hypothesis when in fact it is false. The probability that this occurs is equal to β. Unfortunately, the investigator cannot specify β at the outset because it depends on several factors including the sample size (smaller samples have higher b), the level of significance (β decreases as a increases), and the difference in the parameter under the null and alternative hypothesis.
We noted in several examples in this chapter, the relationship between confidence intervals and tests of hypothesis. The approaches are different, yet related. It is possible to draw a conclusion about statistical significance by examining a confidence interval. For example, if a 95% confidence interval does not contain the null value (e.g., zero when analyzing a mean difference or risk difference, one when analyzing relative risks or odds ratios), then one can conclude that a two-sided test of hypothesis would reject the null at α=0.05. It is important to note that the correspondence between a confidence interval and test of hypothesis relates to a two-sided test and that the confidence level corresponds to a specific level of significance (e.g., 95% to α=0.05, 90% to α=0.10 and so on). The exact significance of the test, the p-value, can only be determined using the hypothesis testing approach and the p-value provides an assessment of the strength of the evidence and not an estimate of the effect.
The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?
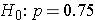
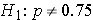
α=0.05
First, determine whether the sample size is adequate.
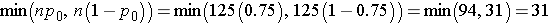
Therefore the sample size is adequate, and we can use the following formula:
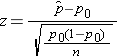
Reject H0 if Z is less than or equal to -1.96 or if Z is greater than or equal to 1.96.
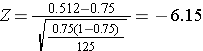
We reject the null hypothesis because -6.15<-1.96. Therefore there is a statistically significant difference in the proportion of children in Boston using dental services compated to the national proportion.