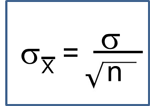Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.

Step 1. Set up hypotheses and select the level of significance α.

H₀: Null hypothesis (no change, no difference);

H₁: Research hypothesis (investigator's belief); α =0.05

Upper-tailed, Lower-tailed, Two-tailed Tests

The research or alternative hypothesis can take one of three forms. An investigator might believe that the parameter has increased, decreased or changed. For example, an investigator might hypothesize:

H₁: μ > μ ₀ , where μ₀ is the comparator or null value (e.g., μ₀ =191 in our example about weight in men in 2006) and an increase is hypothesized - this type of test is called an upper-tailed test;
H₁: μ < μ₀ , where a decrease is hypothesized and this is called a lower-tailed test; or
H₁: μ ≠ μ _0, where a difference is hypothesized and this is called a two-tailed test.

The exact form of the research hypothesis depends on the investigator's belief about the parameter of interest and whether it has possibly increased, decreased or is different from the null value. The research hypothesis is set up by the investigator before any data are collected.

Step 2. Select the appropriate test statistic.

The test statistic is a single number that summarizes the sample information. An example of a test statistic is the Z statistic computed as follows:

equation image indicator

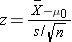
When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

Step 3. Set up decision rule.

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H₀ if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H₀ if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H₀ if the test statistic is smaller than the critical value. In a two-tailed test the decision rule has investigators reject H₀ if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.
The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value. For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.

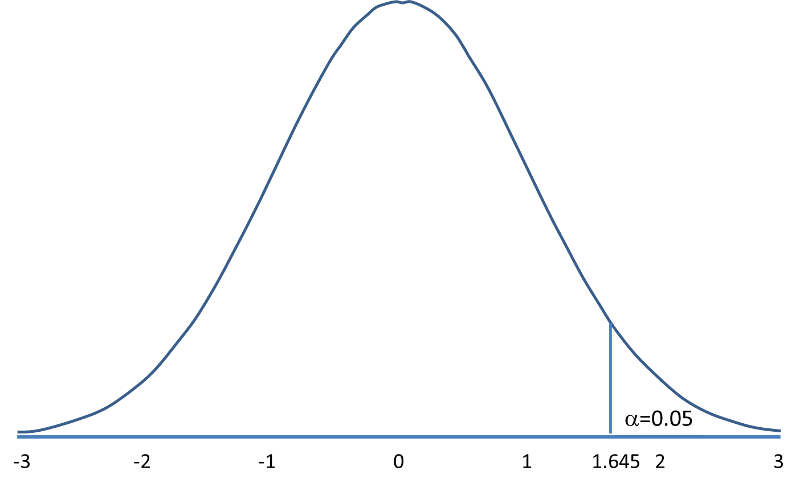
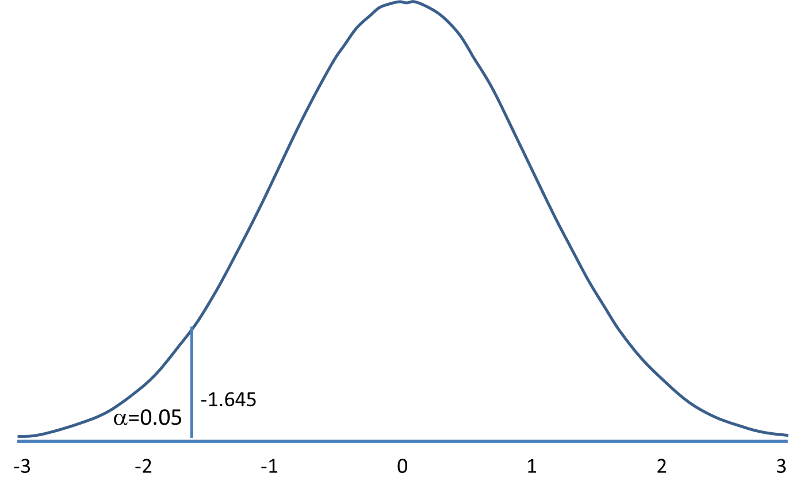
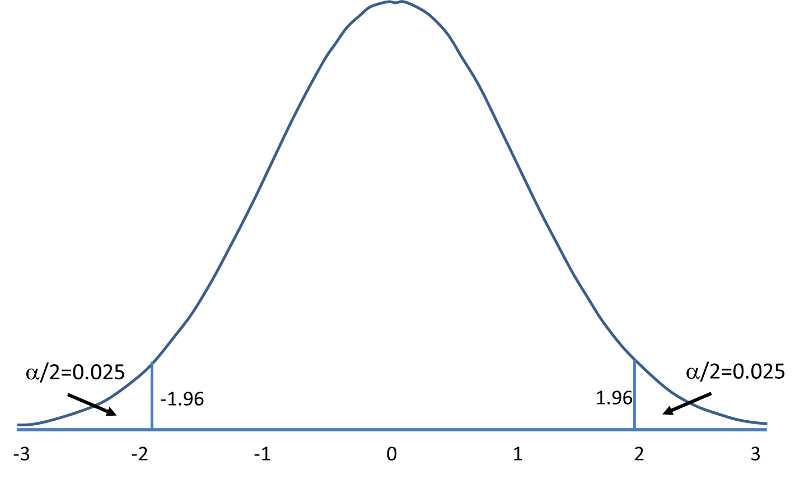
The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Standard normal distribution with upper tail at 1.645 and alpha=0.05

Rejection Region for Upper-Tailed Z Test (H₁: μ > μ₀ ) with α=0.05

The decision rule is: Reject H₀ if Z > 1.645.

Upper-Tailed Test
α	Z
0.10	1.282
0.05	1.645
0.025	1.960
0.010	2.326
0.005	2.576
0.001	3.090
0.0001	3.719

Standard normal distribution with lower tail at -1.645 and alpha=0.05

Rejection Region for Lower-Tailed Z Test (H₁: μ < μ₀ ) with α =0.05

The decision rule is: Reject H₀ if Z < 1.645.

Lower-Tailed Test
a	Z
0.10	-1.282
0.05	-1.645
0.025	-1.960
0.010	-2.326
0.005	-2.576
0.001	-3.090
0.0001	-3.719

Standard normal distribution with two tails

Rejection Region for Two-Tailed Z Test (H₁: μ ≠ μ ₀ ) with α =0.05

The decision rule is: Reject H₀ if Z < -1.960 or if Z > 1.960.

Two-Tailed Test
α	Z
0.20	1.282
0.10	1.645
0.05	1.960
0.010	2.576
0.001	3.291
0.0001	3.819

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

Step 4. Compute the test statistic.

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

Step 5. Conclusion.

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H₀.

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H₀.

Things to Remember When Interpreting P Values

P-values summarize statistical significance and do not address clinical significance. There are instances where results are both clinically and statistically significant - and others where they are one or the other but not both. This is because P-values depend upon both the magnitude of association and the precision of the estimate (the sample size). When the sample size is large, results can reach statistical significance (i.e., small p-value) even when the effect is small and clinically unimportant. Conversely, with small sample sizes, results can fail to reach statistical significance yet the effect is large and potentially clinical important. It is extremely important to assess both statistical and clinical significance of results.
Statistical tests allow us to draw conclusions of significance or not based on a comparison of the p-value to our selected level of significance. Remember that this conclusion is based on the selected level of significance ( α ) and could change with a different level of significance. While α =0.05 is standard, a p-value of 0.06 should be examined for clinical importance.
When conducting any statistical analysis, there is always a possibility of an incorrect conclusion. With many statistical analyses, this possibility is increased. Investigators should only conduct the statistical analyses (e.g., tests) of interest and not all possible tests.
Many investigators inappropriately believe that the p-value represents the probability that the null hypothesis is true. P-values are computed based on the assumption that the null hypothesis is true. The p-value is the probability that the data could deviate from the null hypothesis as much as they did or more. Consequently, the p-value measures the compatibility of the data with the null hypothesis, not the probability that the null hypothesis is correct.
Statistical significance does not take into account the possibility of bias or confounding - these issues must always be investigated.
Evidence-based decision making is important in public health and in medicine, but decisions are rarely made based on the finding of a single study. Replication is always important to build a body of evidence to support findings.

We now use the five-step procedure to test the research hypothesis that the mean weight in men in 2006 is more than 191 pounds. We will assume the sample data are as follows: n=100, 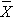equation image indicator =197.1 and s=25.6.

Step 1. Set up hypotheses and determine level of significance

H₀: μ = 191 H₁: μ > 191 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

Step 2. Select the appropriate test statistic.

Because the sample size is large (n>30) the appropriate test statistic is

equation image indicator

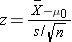
Step 3. Set up decision rule.

In this example, we are performing an upper tailed test (H₁: μ> 191), with a Z test statistic and selected α =0.05. Reject H₀ if Z > 1.645.

Step 4. Compute the test statistic.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

equation image indicator

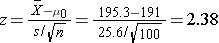
Step 5. Conclusion.

We reject H₀ because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H₀. In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H₀. In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H₀ because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H₀ because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H₀ because 2.38 < 2.576. Therefore, the smallest α where we still reject H₀ is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.

Type I and Type II Errors

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H₀ when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H₀ (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

	Do Not Reject H₀	Reject H₀
H₀ is True	Correct Decision	Type I Error
H₀ is False	Type II Error	Correct Decision

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H₀, then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H₀ that the research hypothesis is true (as it is the more likely scenario when we reject H₀).

When we run a test of hypothesis and decide not to reject H₀ (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H₀ | H₀ is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H₀, it may be very likely that we are committing a Type II error (i.e., failing to reject H₀ when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H₀, we conclude that we do not have significant evidence to show that H₁ is true. We do not conclude that H₀ is true.

Lightbulb icon signifying an important idea

The most common reason for a Type II error is a small sample size.

return to top | previous page | next page