Tests with One Sample, Continuous Outcome
Hypothesis testing applications with a continuous outcome variable in a single population are performed according to the five-step procedure outlined above. A key component is setting up the null and research hypotheses. The objective is to compare the mean in a single population to known mean (μ0). The known value is generally derived from another study or report, for example a study in a similar, but not identical, population or a study performed some years ago. The latter is called a historical control. It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.
It is important in setting up the hypotheses in a one sample test that the mean specified in the null hypothesis is a fair and reasonable comparator. This will be discussed in the examples that follow.
In one sample tests for a continuous outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data - including the sample size (n), the sample mean ( 
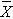 ) and the sample standard deviation (s). We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formulas for test statistics depend on the sample size and are given below.
) and the sample standard deviation (s). We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formulas for test statistics depend on the sample size and are given below.
Test Statistics for Testing H0: μ= μ0
- if n > 30

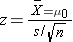
- if n < 30

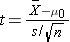 where df=n-1
where df=n-1
Note that statistical computing packages will use the t statistic exclusively and make the necessary adjustments for comparing the test statistic to appropriate values from probability tables to produce a p-value.
Example:
The National Center for Health Statistics (NCHS) published a report in 2005 entitled Health, United States , containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races. The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured. The sample data are summarized as follows: n=100, x̄
, containing extensive information on major trends in the health of Americans. Data are provided for the US population as a whole and for specific ages, sexes and races. The NCHS report indicated that in 2002 Americans paid an average of $3,302 per year on health care and prescription drugs. An investigator hypothesizes that in 2005 expenditures have decreased primarily due to the availability of generic drugs. To test the hypothesis, a sample of 100 Americans are selected and their expenditures on health care and prescription drugs in 2005 are measured. The sample data are summarized as follows: n=100, x̄
=$3,190 and s=$890. Is there statistical evidence of a reduction in expenditures on health care and prescription drugs in 2005? Is the sample mean of $3,190 evidence of a true reduction in the mean or is it within chance fluctuation? We will run the test using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance
H0: μ = 3,302 H1: μ < 3,302 α =0.05
The research hypothesis is that expenditures have decreased, and therefore a lower-tailed test is used.
- Step 2. Select the appropriate test statistic.
Because the sample size is large (n> 30) the appropriate test statistic is

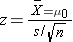
- Step 3. Set up decision rule.
This is a lower tailed test, using a Z statistic and a 5% level of significance. Reject H0 if Z < -1.645.
- Step 4. Compute the test statistic.
We now substitute the sample data into the formula for the test statistic identified in Step 2.

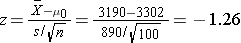
- Step 5. Conclusion.
We do not reject H0 because -1.26 > -1.645. We do not have statistically significant evidence at α=0.05 to show that the mean expenditures on health care and prescription drugs are lower in 2005 than the mean of $3,302 reported in 2002.
Recall that when we fail to reject H0 in a test of hypothesis that either the null hypothesis is true (here the mean expenditures in 2005 are the same as those in 2002 and equal to $3,302) or we committed a Type II error (i.e., we failed to reject H0 when in fact it is false). In summarizing this test, we conclude that we do not have sufficient evidence to reject H0. We do not conclude that H0 is true, because there may be a moderate to high probability that we committed a Type II error. It is possible that the sample size is not large enough to detect a difference in mean expenditures.
Example:
The NCHS reported that the mean total cholesterol level in 2002 for all adults was 203. Total cholesterol levels in participants who attended the seventh examination of the Offspring in the Framingham Heart Study are summarized as follows: n=3,310, x̄ =200.3, and s=36.8. Is there statistical evidence of a difference in mean cholesterol levels in the Framingham Offspring?
Here we want to assess whether the sample mean of 200.3 in the Framingham sample is statistically significantly different from 203 (i.e., beyond what we would expect by chance). We will run the test using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance
H0: μ= 203 H1: μ≠ 203 α=0.05
The research hypothesis is that cholesterol levels are different in the Framingham Offspring, and therefore a two-tailed test is used.
- Step 2. Select the appropriate test statistic.
Because the sample size is large (n>30) the appropriate test statistic is

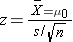
- Step 3. Set up decision rule.
This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H0 if Z < -1.960 or is Z > 1.960.
- Step 4. Compute the test statistic.
We now substitute the sample data into the formula for the test statistic identified in Step 2.

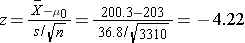
- Step 5. Conclusion.
We reject H0 because -4.22 ≤ -1. .960. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level in the Framingham Offspring is different from the national average of 203 reported in 2002. Because we reject H0, we also approximate a p-value. Using the two-sided significance levels, p < 0.0001.
Statistical Significance versus Clinical (Practical) Significance
This example raises an important concept of statistical versus clinical or practical significance. From a statistical standpoint, the total cholesterol levels in the Framingham sample are highly statistically significantly different from the national average with p < 0.0001 (i.e., there is less than a 0.01% chance that we are incorrectly rejecting the null hypothesis). However, the sample mean in the Framingham Offspring study is 200.3, less than 3 units different from the national mean of 203. The reason that the data are so highly statistically significant is due to the very large sample size. It is always important to assess both statistical and clinical significance of data. This is particularly relevant when the sample size is large. Is a 3 unit difference in total cholesterol a meaningful difference?
Example:
Consider again the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. Suppose a new drug is proposed to lower total cholesterol. A study is designed to evaluate the efficacy of the drug in lowering cholesterol. Fifteen patients are enrolled in the study and asked to take the new drug for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows: n=15, x̄ =195.9 and s=28.7. Is there statistical evidence of a reduction in mean total cholesterol in patients after using the new drug for 6 weeks? We will run the test using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance
H0: μ= 203 H1: μ< 203 α=0.05
- Step 2. Select the appropriate test statistic.
Because the sample size is small (n<30) the appropriate test statistic is

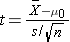 .
.
- Step 3. Set up decision rule.
This is a lower tailed test, using a t statistic and a 5% level of significance. In order to determine the critical value of t, we need degrees of freedom, df, defined as df=n-1. In this example df=15-1=14. The critical value for a lower tailed test with df=14 and a =0.05 is -2.145 and the decision rule is as follows: Reject H0 if t < -2.145.
- Step 4. Compute the test statistic.
We now substitute the sample data into the formula for the test statistic identified in Step 2.

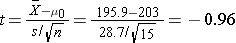
- Step 5. Conclusion.
We do not reject H0 because -0.96 > -2.145. We do not have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower than the national mean in patients taking the new drug for 6 weeks. Again, because we failed to reject the null hypothesis we make a weaker concluding statement allowing for the possibility that we may have committed a Type II error (i.e., failed to reject H0 when in fact the drug is efficacious).

This example raises an important issue in terms of study design. In this example we assume in the null hypothesis that the mean cholesterol level is 203. This is taken to be the mean cholesterol level in patients without treatment. Is this an appropriate comparator? Alternative and potentially more efficient study designs to evaluate the effect of the new drug could involve two treatment groups, where one group receives the new drug and the other does not, or we could measure each patient's baseline or pre-treatment cholesterol level and then assess changes from baseline to 6 weeks post-treatment. These designs are also discussed here.
Video - Comparing a Sample Mean to Known Population Mean (8:20)
Link to transcript of the video