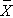Tests with Two Independent Samples, Continuous Outcome
There are many applications where it is of interest to compare two independent groups with respect to their mean scores on a continuous outcome. Here we compare means between groups, but rather than generating an estimate of the difference, we will test whether the observed difference (increase, decrease or difference) is statistically significant or not. Remember, that hypothesis testing gives an assessment of statistical significance, whereas estimation gives an estimate of effect and both are important.
Here we discuss the comparison of means when the two comparison groups are independent or physically separate. The two groups might be determined by a particular attribute (e.g., sex, diagnosis of cardiovascular disease) or might be set up by the investigator (e.g., participants assigned to receive an experimental treatment or placebo). The first step in the analysis involves computing descriptive statistics on each of the two samples. Specifically, we compute the sample size, mean and standard deviation in each sample and we denote these summary statistics as follows:
for sample 1:
- n1

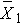
- s1
for sample 2:
- n2


- s2
The designation of sample 1 and sample 2 is arbitrary. In a clinical trial setting the convention is to call the treatment group 1 and the control group 2. However, when comparing men and women, for example, either group can be 1 or 2.
In the two independent samples application with a continuous outcome, the parameter of interest in the test of hypothesis is the difference in population means, μ1-μ2. The null hypothesis is always that there is no difference between groups with respect to means, i.e.,

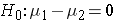
The null hypothesis can also be written as follows: H0: μ1 = μ2. In the research hypothesis, an investigator can hypothesize that the first mean is larger than the second (H1: μ1 > μ2 ), that the first mean is smaller than the second (H1: μ1 < μ2 ), or that the means are different (H1: μ1 ≠ μ2 ). The three different alternatives represent upper-, lower-, and two-tailed tests, respectively. The following test statistics are used to test these hypotheses.
Test Statistics for Testing H0: μ1 = μ2
- if n1 > 30 and n2 > 30

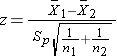
- if n1 < 30 or n2 < 30

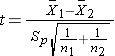 where df =n1+n2-2.
where df =n1+n2-2.
NOTE: The formulas above assume equal variability in the two populations (i.e., the population variances are equal, or s12 = s22). This means that the outcome is equally variable in each of the comparison populations. For analysis, we have samples from each of the comparison populations. If the sample variances are similar, then the assumption about variability in the populations is probably reasonable. As a guideline, if the ratio of the sample variances, s12/s22 is between 0.5 and 2 (i.e., if one variance is no more than double the other), then the formulas above are appropriate. If the ratio of the sample variances is greater than 2 or less than 0.5 then alternative formulas must be used to account for the heterogeneity in variances.
The test statistics include Sp, which is the pooled estimate of the common standard deviation (again assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples as follows:

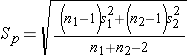
Because we are assuming equal variances between groups, we pool the information on variability (sample variances) to generate an estimate of the variability in the population. Note: Because Sp is a weighted average of the standard deviations in the sample, Sp will always be in between s1 and s2.)
Example:
Data measured on n=3,539 participants who attended the seventh examination of the Offspring in the Framingham Heart Study are shown below.
|
|
Men |
Women |
||||
|
Characteristic |
n |
|
S |
n |
|
s |
|
Systolic Blood Pressure |
1,623 |
128.2 |
17.5 |
1,911 |
126.5 |
20.1 |
|
Diastolic Blood Pressure |
1,622 |
75.6 |
9.8 |
1,910 |
72.6 |
9.7 |
|
Total Serum Cholesterol |
1,544 |
192.4 |
35.2 |
1,766 |
207.1 |
36.7 |
|
Weight |
1,612 |
194.0 |
33.8 |
1,894 |
157.7 |
34.6 |
|
Height |
1,545 |
68.9 |
2.7 |
1,781 |
63.4 |
2.5 |
|
Body Mass Index |
1,545 |
28.8 |
4.6 |
1,781 |
27.6 |
5.9 |
Suppose we now wish to assess whether there is a statistically significant difference in mean systolic blood pressures between men and women using a 5% level of significance.
- Step 1. Set up hypotheses and determine level of significance
H0: μ1 = μ2
H1: μ1 ≠ μ2 α=0.05
- Step 2. Select the appropriate test statistic.
Because both samples are large (> 30), we can use the Z test statistic as opposed to t. Note that statistical computing packages use t throughout. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The guideline suggests investigating the ratio of the sample variances, s12/s22. Suppose we call the men group 1 and the women group 2. Again, this is arbitrary; it only needs to be noted when interpreting the results. The ratio of the sample variances is 17.52/20.12 = 0.76, which falls between 0.5 and 2 suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is

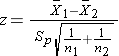 .
.
- Step 3. Set up decision rule.
This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H0 if Z < -1.960 or is Z > 1.960.
- Step 4. Compute the test statistic.
We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.

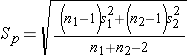

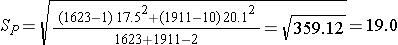
Notice that the pooled estimate of the common standard deviation, Sp, falls in between the standard deviations in the comparison groups (i.e., 17.5 and 20.1). Sp is slightly closer in value to the standard deviation in the women (20.1) as there were slightly more women in the sample. Recall, Sp is a weight average of the standard deviations in the comparison groups, weighted by the respective sample sizes.
Now the test statistic:

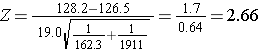
- Step 5. Conclusion.
We reject H0 because 2.66 > 1.960. We have statistically significant evidence at α=0.05 to show that there is a difference in mean systolic blood pressures between men and women. The p-value is p < 0.010.
Here again we find that there is a statistically significant difference in mean systolic blood pressures between men and women at p < 0.010. Notice that there is a very small difference in the sample means (128.2-126.5 = 1.7 units), but this difference is beyond what would be expected by chance. Is this a clinically meaningful difference? The large sample size in this example is driving the statistical significance. A 95% confidence interval for the difference in mean systolic blood pressures is: 1.7 + 1.26 or (0.44, 2.96). The confidence interval provides an assessment of the magnitude of the difference between means whereas the test of hypothesis and p-value provide an assessment of the statistical significance of the difference.
Above we performed a study to evaluate a new drug designed to lower total cholesterol. The study involved one sample of patients, each patient took the new drug for 6 weeks and had their cholesterol measured. As a means of evaluating the efficacy of the new drug, the mean total cholesterol following 6 weeks of treatment was compared to the NCHS-reported mean total cholesterol level in 2002 for all adults of 203. At the end of the example, we discussed the appropriateness of the fixed comparator as well as an alternative study design to evaluate the effect of the new drug involving two treatment groups, where one group receives the new drug and the other does not. Here, we revisit the example with a concurrent or parallel control group, which is very typical in randomized controlled trials or clinical trials (refer to the EP713 module on Clinical Trials).
Example:
A new drug is proposed to lower total cholesterol. A randomized controlled trial is designed to evaluate the efficacy of the medication in lowering cholesterol. Thirty participants are enrolled in the trial and are randomly assigned to receive either the new drug or a placebo. The participants do not know which treatment they are assigned. Each participant is asked to take the assigned treatment for 6 weeks. At the end of 6 weeks, each patient's total cholesterol level is measured and the sample statistics are as follows.
|
Treatment |
Sample Size |
Mean |
Standard Deviation |
|---|---|---|---|
|
New Drug |
15 |
195.9 |
28.7 |
|
Placebo |
15 |
227.4 |
30.3 |
Is there statistical evidence of a reduction in mean total cholesterol in patients taking the new drug for 6 weeks as compared to participants taking placebo? We will run the test using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance
H0: μ1 = μ2 H1: μ1 < μ2 α=0.05
- Step 2. Select the appropriate test statistic.
Because both samples are small (< 30), we use the t test statistic. Before implementing the formula, we first check whether the assumption of equality of population variances is reasonable. The ratio of the sample variances, s12/s22 =28.72/30.32 = 0.90, which falls between 0.5 and 2, suggesting that the assumption of equality of population variances is reasonable. The appropriate test statistic is:

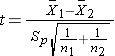 .
.
- Step 3. Set up decision rule.
This is a lower-tailed test, using a t statistic and a 5% level of significance. The appropriate critical value can be found in the t Table (in More Resources to the right). In order to determine the critical value of t we need degrees of freedom, df, defined as df=n1+n2-2 = 15+15-2=28. The critical value for a lower tailed test with df=28 and α=0.05 is -1.701 and the decision rule is: Reject H0 if t < -1.701.
- Step 4. Compute the test statistic.
We now substitute the sample data into the formula for the test statistic identified in Step 2. Before substituting, we will first compute Sp, the pooled estimate of the common standard deviation.

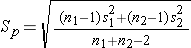

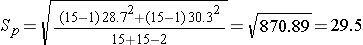
Now the test statistic,

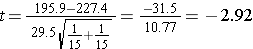
- Step 5. Conclusion.
We reject H0 because -2.92 < -1.701. We have statistically significant evidence at α=0.05 to show that the mean total cholesterol level is lower in patients taking the new drug for 6 weeks as compared to patients taking placebo, p < 0.005.
The clinical trial in this example finds a statistically significant reduction in total cholesterol, whereas in the previous example where we had a historical control (as opposed to a parallel control group) we did not demonstrate efficacy of the new drug. Notice that the mean total cholesterol level in patients taking placebo is 217.4 which is very different from the mean cholesterol reported among all Americans in 2002 of 203 and used as the comparator in the prior example. The historical control value may not have been the most appropriate comparator as cholesterol levels have been increasing over time. In the next section, we present another design that can be used to assess the efficacy of the new drug.
Video - Comparison of Two Independent Samples With a Continuous Outcome (8:02)
Link to transcript of the video