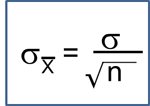Time to Event Variables
There are unique features of time to event variables. First, times to event are always positive and their distributions are often skewed. For example, in a study assessing time to relapse in high risk patients, the majority of events (relapses) may occur early in the follow up with very few occurring later. On the other hand, in a study of time to death in a community based sample, the majority of events (deaths) may occur later in the follow up. Standard statistical procedures that assume normality of distributions do not apply. Nonparametric procedures could be invoked except for the fact that there are additional issues. Specifically, complete data (actual time to event data) is not always available on each participant in a study. In many studies, participants are enrolled over a period of time (months or years) and the study ends on a specific calendar date. Thus, participants who enroll later are followed for a shorter period than participants who enroll early. Some participants may drop out of the study before the end of the follow-up period (e.g., move away, become disinterested) and others may die during the follow-up period (assuming the outcome of interest is not death).
In each of these instances, we have incomplete follow-up information. True survival time (sometimes called failure time) is not known because the study ends or because a participant drops out of the study before experiencing the event. What we know is that the participants survival time is greater than their last observed follow-up time. These times are called censored times.
Censoring
There are several different types of censoring. The most common is called right censoring and occurs when a participant does not have the event of interest during the study and thus their last observed follow-up time is less than their time to event. This can occur when a participant drops out before the study ends or when a participant is event free at the end of the observation period.
In the first instance, the participants observed time is less than the length of the follow-up and in the second, the participant's observed time is equal to the length of the follow-up period. These issues are illustrated in the following examples.
Example:
A small prospective study is run and follows ten participants for the development of myocardial infarction (MI, or heart attack) over a period of 10 years. Participants are recruited into the study over a period of two years and are followed for up to 10 years. The graphic below indicates when they enrolled and what subsequently happened to them during the observation period.
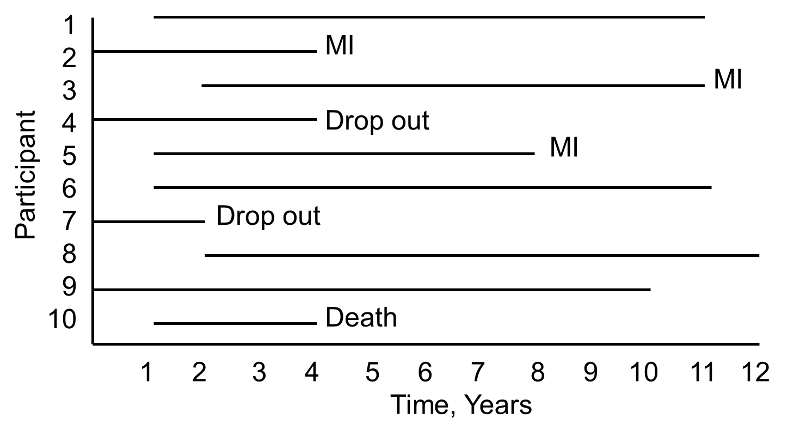
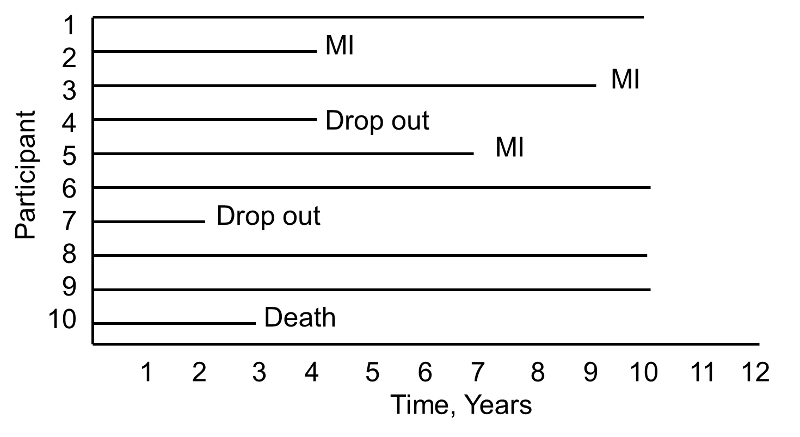
During the study period, three participants suffer myocardial infarction (MI), one dies, two drop out of the study (for unknown reasons), and four complete the 10-year follow-up without suffering MI. The figure below shows the same data, but shows survival time starting at a common time zero (i.e., as if all participants enrolled in the study at the same time).
Based on this data, what is the likelihood that a participant will suffer an MI over 10 years? Three of 10 participants suffer MI over the course of follow-up, but 30% is probably an underestimate of the true percentage as two participants dropped out and might have suffered an MI had they been observed for the full 10 years. Their observed times are censored. In addition, one participant dies after 3 years of follow-up. Should these three individuals be included in the analysis, and if so, how?
If we exclude all three, the estimate of the likelihood that a participant suffers an MI is 3/7 = 43%, substantially higher than the initial estimate of 30%. The fact that all participants are often not observed over the entire follow-up period makes survival data unique. In this small example, participant 4 is observed for 4 years and over that period does not have an MI. Participant 7 is observed for 2 years and over that period does not have an MI. While they do not suffer the event of interest, they contribute important information. Survival analysis techniques make use of this information in the estimate of the probability of event.
|
An important assumption is made to make appropriate use of the censored data. Specifically, we assume that censoring is independent or unrelated to the likelihood of developing the event of interest. This is called non-informative censoring and essentially assumes that the participants whose data are censored would have the same distribution of failure times (or times to event) if they were actually observed. |
Now consider the same study and the experiences of 10 different participants as depicted below.
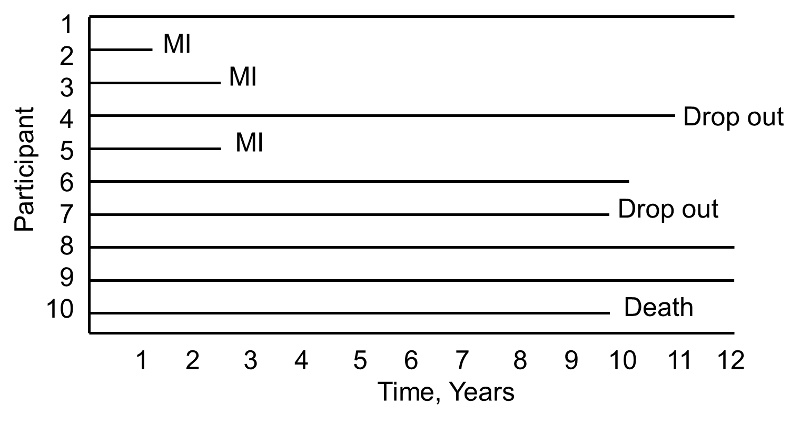
Notice here that, once again, three participants suffer MI, one dies, two drop out of the study, and four complete the 10-year follow-up without suffering MI. However, the events (MIs) occur much earlier, and the drop outs and death occur later in the course of follow-up. Should these differences in participants experiences affect the estimate of the likelihood that a participant suffers an MI over 10 years?
In survival analysis we analyze not only the numbers of participants who suffer the event of interest (a dichotomous indicator of event status), but also the times at which the events occur.