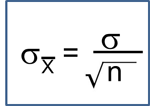Author:
Lisa Sullivan, PhD
Professor of Biostatistics
Boston University School of Public Health
Introduction
As noted in earlier modules a key goal in applied biostatistics is to make inferences about unknown population parameters based on sample statistics. There are two broad areas of statistical inference, estimation and hypothesis testing. Estimation is the process of determining a likely value for a population parameter (e.g., the true population mean or population proportion) based on a random sample. In practice, we select a sample from the target population and use sample statistics (e.g., the sample mean or sample proportion) as estimates of the unknown parameter. The sample should be representative of the population, with participants selected at random from the population. In generating estimates, it is also important to quantify the precision of estimates from different samples.
Learning Objectives
After completing this module, the student will be able to:
- Define point estimate, standard error, confidence level and margin of error
- Compare and contrast standard error and margin of error
- Compute and interpret confidence intervals for means and proportions
- Differentiate independent and matched or paired samples
- Compute confidence intervals for the difference in means and proportions in independent samples and for the mean difference in paired samples
- Identify the appropriate confidence interval formula based on type of outcome variable and number of samples
