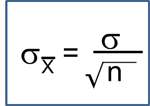Summary
This module focused on the formulas for estimating different unknown population parameters. In each application, a random sample or two independent random samples were selected from the target population and sample statistics (e.g., sample sizes, means, and standard deviations or sample sizes and proportions) were generated. Point estimates are the best single-valued estimates of an unknown population parameter. Because these can vary from sample to sample, most investigations start with a point estimate and build in a margin of error. The margin of error quantifies sampling variability and includes a value from the Z or t distribution reflecting the selected confidence level as well as the standard error of the point estimate. It is important to remember that the confidence interval contains a range of likely values for the unknown population parameter; a range of values for the population parameter consistent with the data. It is also possible, although the likelihood is small, that the confidence interval does not contain the true population parameter. This is important to remember in interpreting intervals. Confidence intervals are also very useful for comparing means or proportions and can be used to assess whether there is a statistically meaningful difference. This is based on whether the confidence interval includes the null value (e.g., 0 for the difference in means, mean difference and risk difference or 1 for the relative risk and odds ratio).
The precision of a confidence interval is defined by the margin of error (or the width of the interval). A larger margin of error (wider interval) is indicative of a less precise estimate. For example, suppose we estimate the relative risk of complications from an experimental procedure compared to the standard procedure of 5.7. This estimate indicates that patients undergoing the new procedure are 5.7 times more likely to suffer complications. Suppose that the 95% confidence interval is (0.4, 12.6). The confidence interval suggests that the relative risk could be anywhere from 0.4 to 12.6 and because it includes 1 we cannot conclude that there is a statistically significantly elevated risk with the new procedure. Suppose the same study produced an estimate of a relative risk of 2.1 with a 95% confidence interval of (1.5, 2.8). This second study suggests that patients undergoing the new procedure are 2.1 times more likely to suffer complications. However, because the confidence interval here does not contain the null value 1, we can conclude that this is a statistically elevated risk. We will discuss this idea of statistical significance in much more detail in Chapter 7.
The following summary provides the key formulas for confidence interval estimates in different situations.
- Confidence interval for a mean (μ) from one sample
For n > 30 use the z-table with this equation : 
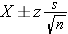
For n<30 use the t-table with degrees of freedom (df)=n-1
- Confidence interval for the difference in means (μ1-μ2) from two independent samples
If n1 > 30 and n2 > 30, use the z-table with this equation: 
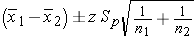
If n1 < 30 or n2 < 30, use the t-table with degrees of freedom = n1+n2-2.
For both large and small samples Sp is the pooled estimate of the common standard deviation (assuming that the variances in the populations are similar) computed as the weighted average of the standard deviations in the samples.

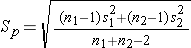
- Confidence interval for the difference in a continuous outcome (μd) with two matched or paired samples
If n > 30, use 
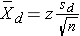 and use the z-table for standard normal distribution
and use the z-table for standard normal distribution
If n < 30, use the t-table with degrees of freedom (df)=n-1
- Confidence interval for a proportion from one sample (p) with a dichotomous outcome
- Confidence interval for a risk difference (RD) calculated from two independent samples

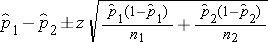
- Confidence interval for a risk ratio (RR) or prevalence ratio from two independent samples
RR = p1/p2

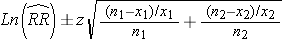
Then take exp[lower limit of Ln(RR)] and exp[upper limit of Ln(RR)] to get the lower and upper limits of the confidence interval for RR.
- Confidence interval for an odds ratio (OR)

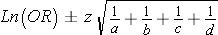
Then take exp[lower limit of Ln(OR)] and exp[upper limit of Ln(OR)] to get the lower and upper limits of the confidence interval for OR.
Note that this summary table only provides formulas for larger samples. As noted throughout the modules alternative formulas must be used for small samples.