Exponents

You can think of exponents as a shorthand notation indicating "power" or the number of times a quantity is multiplied times itself. Exponential or "scientific notation" provides a much easier way to express and think about very large or very small quantities. In addition, an understanding of exponents and logarithms is essential to effective use of methods such as multiple logistic regression.

Examples:

2 * 2 = 2² (Read as "two squared") = 4

2*2*2 = 2³ (Read as "two cubed") = 8

8⁵ = 8*8*8*8*8 = 32,768

Logarithms

Logarithms are the "opposite" or the inverse of exponentials. In a sense logarithms undo what exponentiation does.

Suppose that if one raises a base number "b" to the "x" power, the result is "y". If so, then the log (for base b) of "y" is "x".Another way to think about logarithms is that a positive logarithm is how many times you have to multiple the base to get a particular number.

For example:

2⁴ = 2*2*2*2 =16, i.e., the base number 2 exponentiated to the 4^th power is 16.

This relationship could also be expressed as

log₂(16) = 4, meaning the base 2 log of 16 is 4, i.e., in order to get 16, one would have to raise the base number 2 to the 4^th power.

Conversely, a negative logarithm is how many times you multiple by the inverse of the base to get the number. For example,

Log₁₀(0.001)= - 3, i.e., 1/10*1/10*1/10 = 1/1,000

Another example: log₆(216) = ?

This asks, to what power would the base number 6 need to be raised in order to get 216? We can start multiplying 6 to determine that 6*6 = 36 and 36*6 = 216. So, the answer is 3. One would have to raise the base 6 to the 3^rd power to get 216.

This could be expressed with these two equivalent statements:

y = b^x is equivalent to log_b(y) = x

The value of the subscripted "b" is the base of the logarithm. There are many possible "bases" that can be used, but there are two bases that are particularly useful in practical terms.

Base 10 is used for "common logarithms" or common log
Base "e" is the "natural logarithm", where "e" ≈ 2.71828

Common Logarithms

Common logs use the base 10. They are for some scales, for example those that measure acidity (pH scale), sound amplitude (decibel scale), and the intensity of earthquakes (the Richter scale). One way to think about common logs is that a positive logarithm is how many times you have to multiple the base to get a particular number. For example:

Log₁₀(1,000) = 3, i.e., 10*10*10 = 1,000
Log₁₀(1,000,000) = 6, I.e., 10*10*10*10*10*10 = 1,000,000

Numbers Expressed Exponentially & as Logarithms

Number	Exponential Expression	Logarithm (base 10)
1000	10³	3
100	10²	2
10	10¹	1
1	10⁰	0
1/10 = 0.1	10^-¹	-1
1/100 = 0.01	10^-²	-2
1/1000 = 0.001	10^-³	-3

Acidity (pH scale)

Acidity is based on the molar concentration of hydrogen ions in a solution, and it is defined as:

pH = -log₁₀ [Hydrogen ion concentration]

Example: What is the pH of an aqueous solution when the concentration of hydrogen ion is 5.0 x 10^-⁴ M?

pH = -log [H⁺] = -log (5.0 x 10^-⁴) = - (-3.30) = 3.30

Pure water has a pH value of 7. Since acidity is based on a log₁₀ scale, another way of thinking about this is that each whole pH value below 7 is ten times more acidic than the next higher value. For example, urine generally has a hydrogen ion concentration 10 times greater than that of pure water, and -log₁₀ [10] = -1, so the pH of urine is 7-1 = 6.

Vinegar is 100,000 times more acidic than water, and -log₁₀ [100,000] = -5, so the pH of vinegar is 7-5 = 2.
Sulfuric acid has a hydrogen ion concentration 1,000,000 times that of pure water, and -log₁₀ [1,000,000] = -6, so the pH of urine is 7-6 = 1.

The same holds true for pH values above 7, each of which has a hydrogen ion concentration ten times less than that the next lowest pH unit.

Bleach, for example, has a hydrogen ion concentration of 0.000001 that of pure water, and -log₁₀ [0.000001] = 6, so the pH of urine is 7+6 = 13.

Exponential Notation

Exponential notation, or scientific notation, is sometimes used to describe disease frequency. We previously computed the prevalence of HIV+ residents of Massachusetts in 2003. Recall that there were 8,263 HIV+ people living in Massachusetts. The total population of Massachusetts, based on census data, was 5.7 million. The prevalence of a condition is the proportion of the population (or group) that has the condition. Therefore, the prevalence of HIV in Massachusetts in 2003 can be calculated with a hand-held calculator or a spreadsheet:

8,263 / 5,700,000 = 0.001449649122807

In essence, the decimal fraction that results represents the frequency per resident, which is certainly not an intuitive way to think about prevalence in a population. It would make much more sense to think about this as the number of people who were HIV+ in some representative group, say per 10,000 residents or perhaps per 100,000 residents. In addition, the calculator has extended the results of the division to a ridiculous number of decimal places. We can simplify this by first rounding off the result.

0.001449649122807 can be rounded off to 0.00145

Next, we can convert this to a more intuitive expression. The decimal fraction is the frequency per person; If we want to express it as the frequency per 10,000 residents, we would multiply by 100,000 by moving the decimal point to the right 5 places.

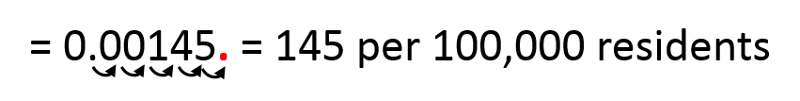
Note that this can be expressed in exponential, i.e.,scientific, notation as 1.45 x 10 ^-3 or 14.5 x 10^-4 or as 145 x 10^-5 which is equivalent to 145 per 100,000 residents. All of these are equivalent expressions.

0.00145 = 145 x 10^-5 = 145 per 100,000 residents

Natural Logarithms

Natural logs use a special base which turns out to be very useful when dealing with exponential growth or decay. Natural logs use the base "e" which is a constant with an approximate value of 2.71828. Like the constant "pi" (p), "e" is an irrational number that goes on forever when expressed as a decimal.

Expressed another way:

From http://betterexplained.com/articles/an-intuitive-guide-to-exponential-functions-e/

"e is the base rate of growth shared by all continually growing processes. e lets you take a simple growth rate (where all change happens at the end of the year) and find the impact of compound, continuous growth, where every nanosecond (or faster) you are growing just a little bit.

e shows up whenever systems grow exponentially and continuously: population, radioactive decay, interest calculations, [etc.]"

e^x lets us plug in time and get growth.
ln(x) lets us plug in growth and get the time it would take.

For example:

e^3 is 20.08. After 3 units of time, we end up with 20.08 times what we started with.
ln(20.08) is about 3. If we want growth of 20.08, we'd wait 3 units of time (again, assuming a 100% continuous growth rate).

e³ = 2.71828 * 2.71828 * 2.71828 = 20.085496, and conversely, log_e(20.085496) = 3

However, to avoid confusion the natural log of "x" is written as "ln(x)" rather than log_e(x), the preceding expression would be written ln(20.085496) = 3.

It is often desirable to estimate the precision of estimates used in public health, such as risk ratios and odds ratios. Techniques for evaluating precision rely on the assumption that the values are normally distributed, i.e. that the distribution of possible values is similar to a bell-shaped curve. However, estimates of risk ratios and odds ratios are generally not normally distributed; they are skewed toward a value of 1, but could be much higher. One of the common methods of "normalizing" distributions like this is to transform the data into a logarithmic distribution. For example, if we examined the frequency of hospital length of stay for most conditions, we would find that it generally conformed to a distribution that is skewed toward shorter lengths of stay with progressively fewer patients having longer stays. However, taking the natural logarithm of length of stay tends to make the distribution more symmetrical.

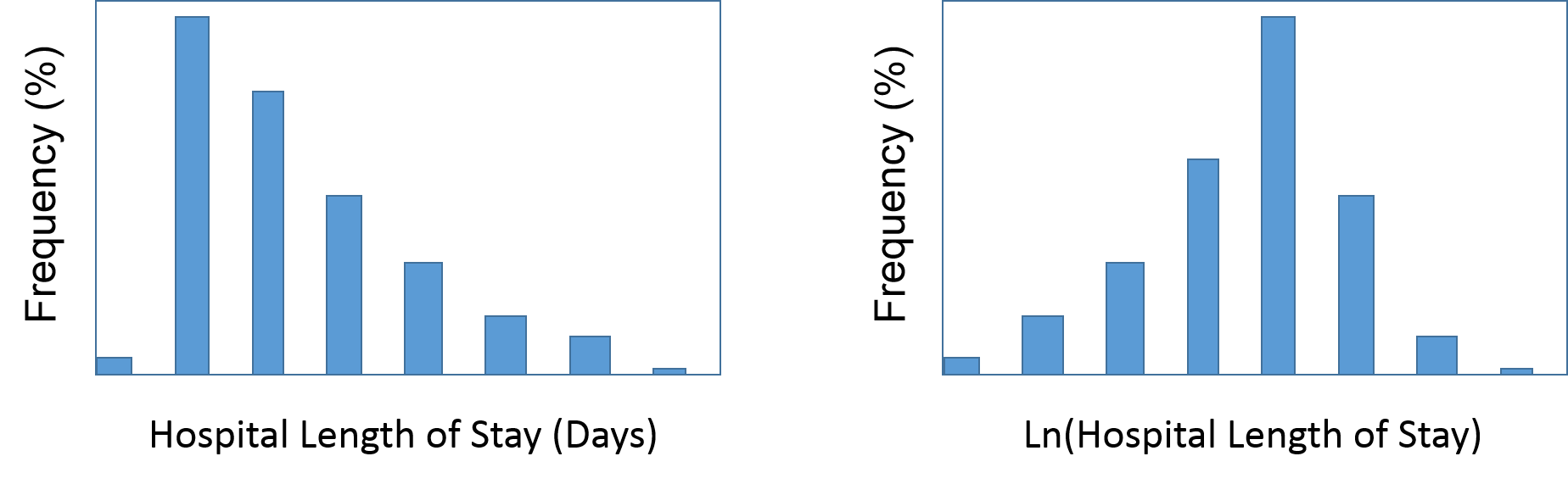
As a result, estimation of the precision of some parameters in public health is facilitated by the use of natural logarithms.

Exponents & Logarithms with Excel

Video (5 min)

return to top | previous page