Fractions, Decimals, and Percentages

The British Medical Journal reported on 123 confirmed cases of H7N9 avian flu (bird flu) admitted to hospitals. They reported that 44 of these individuals died as a result of their infection. This proportion represents a case-fatality rate , and, like all proportions, it can be reported in several ways:

This decimal fraction can be computed manually, in a spreadsheet, on a simple hand-held calculator, or by using the calculator on a smart phone.

Visually we can represent this with the pie chart below.

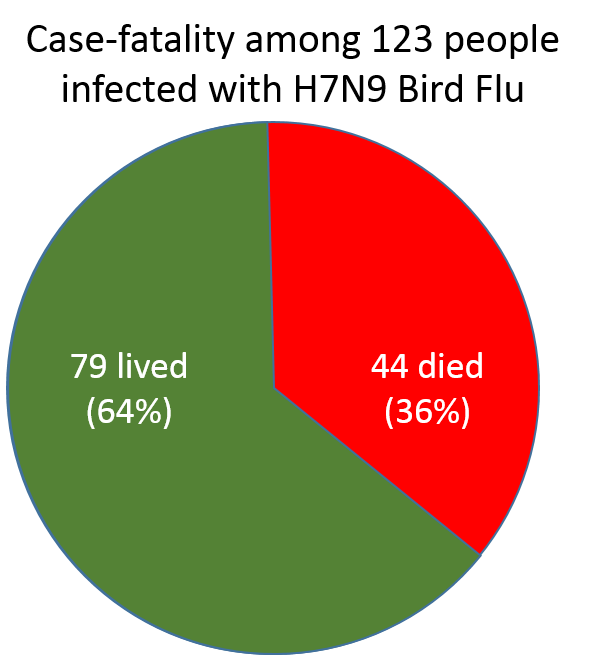
The sample consisted of 123 people with documented bird flu. The fraction of the sample that died was 44/123 = 0.36.

This can also be expressed at 36%. Percent means "per 100." It is a way of standardizing the results to make them easier to compare among different groups or at different times. The actual sample consisted of 123 people, but by expressing the case-fatality rate as a percent, we are saying that in a group of 100 people this frequency would be equivalent to 36 deaths.

 

Question: Data from the Massachusetts Department of Health indicates that in 2003 there were 8,263 people in Massachusetts known to be HIV positive. The estimated population size at the time was 5,700,000 (5.7 million). What was the estimated frequency of HIV expressed as a decimal fraction?

Answer

 

 

How would the frequency of HIV seropositivity be expressed as a percent?

 
 
 
 
 

In this problem the frequency can be expressed as a simple fraction (8,263/5,700,000) or as the equivalent decimal fraction (0.00145). When we compute the decimal fraction, we divide the total number of HIV+ people by the total number of people in the population of Massachusetts. In fact, we are computing the prevalence of HIV seropositivity in Massachusetts. If we want to express this as a percentage, i.e., per 100 people, we would move the decimal point to the right by two places.

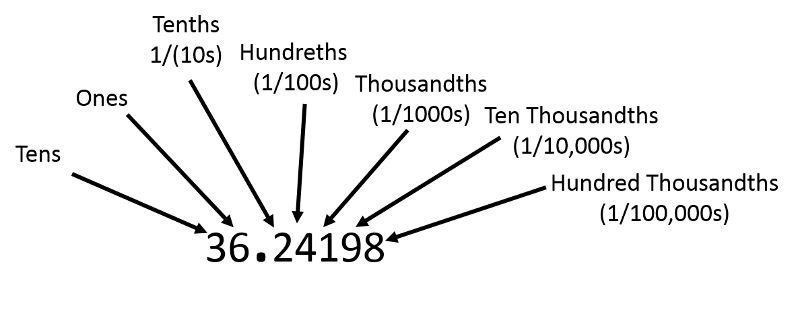
One can think of the decimal point as giving a frame of reference for the magnitude of what we are focusing on.

For example, consider the number 36.241983. This can be thought of as consisting of

3 tens,

6 ones,

2 tenths,

4 hundredths,

1 thousandth,

9 ten thousandths, and

8 hundred thousandths. 

Converting the Frequency Scale

If we go back to the prevalence of HIV in Massachusetts, the decimal fraction provided the frequency per person (e.g., a probability of HIV+ of 0.00145 per person), but this is not an intuitive way to think about prevalence, and there are more convenient ways to express this, as summarized in the table below.

 0.00145 per 1 person.

      0.0145 per 10 persons

        0.145  per 100 persons

           1.45 per 1,000 persons

           14.5 per 10,000 persons

           145 per 100,000 persons

Note that the third expression is "per 100," so this represents a percentage. However, if we wanted to communicate this information to the general public, it might be more intuitive to express this using either of the last two expressions, e.g., "Among 100,000 residents of Massachusetts, about 145 are known to be HIV positive." The first decimal fraction is what you would get when you divided (8,263/5,700,000); to convert this to the last expression, one moves the decimal point 5 places to the right to get 145 per 100,000. As easy way to remember this conversion is that we moved the decimal 5 places to the right to get a convenient whole number of people, and we expressed this as "per 100,000." Note that 100,000 has 5 "0"s after the 1, because we moved the decimal 5 places.

Percent Change

Percent change implies a starting value and an ending value. By convention the percent change is calculated by computing the change in value (i.e., the final value minus the starting value) and dividing the change by the starting value and multiplying the result times 100 in order to express it as a percentage.

 

 

Example 1: In 1960 the prevalence of type 2 diabetes was 10 per 1,000 population, and by 2010 the prevalence had increased to 60 per 1,000 population. What was the percent change?

% Change = (Final value - Starting Value) / Starting Value x 100

= [(60/1,000-10/1,000) / 10/1,000] * 100= [(60 - 10) / 10] * 100 = 5 * 100

= 500% increase

 

Example 2: Investigators created a risk reduction program for truck drivers in Kenya in order to decrease the spread of HIV and other sexually transmitted infections. During a one year follow up period the incidence of sexually transmitted diseases declined from

34 per 100 person years to 20 per 100 person-years. What was the percent change?

% Change = (Final value - Starting Value) / Starting Value x 100

= [(20/ 100 person-years - 34/100 person-years) / 34/100 PERSON-YEARS] * 100

= [-14 / 34] * 100

= - 0.41 * 100

= - 41%, i.e., it declined by 41%

 

 

Currently, under a hypothetical health insurance plan, patients have a $20 copayment for physician office visits.  During the current enrollment period, the enrolled population uses 2.0 visits per capita.  Suppose that for the next enrollment period, the copayment goes up to $25 per office visit.  The health insurer estimates that the enrollees will use only 1.8 visits per capita with the new copayment. 

What is the percent change in the copayment? 

 
 
 
 

 

Currently, under a hypothetical health insurance plan, patients have a $20 copayment for physician office visits.  During the current enrollment period, the enrolled population uses 2.0 visits per capita.  Suppose that for the next enrollment period, the copayment goes up to $25 per office visit.  The health insurer estimates that the enrollees will use only 1.8 visits per capita with the new copayment. 

 What is the percent change in the number of visits per capita? 

 
 
 
 

 

 


return to top | previous page | next page