Some Basic Algebra
In this section we will review some of the simple, basic concepts for solving algebraic equations. It is often possible to express quantitative problems with algebraic equations or expressions. This provides a useful shorthand way of laying the problem out in a way that makes it easier to see relationships, identify the information that is needed, and then solve the problem. The steps illustrated here provide some very simple, fundamental operations that can facilitate your ability to simplify algebraic expressions and then solve them to determine the value of the unknown variables that hold the answer to the problem.
Example:
Consider the simple equation x + 20 = 45. The equal sign indicates that the two sides of the equation are equivalent or equally balanced. This means that we can manipulate the equation, and, provided we do the same thing to both sides of the equation, the balance will not be upset.
In this simple example we could subtract 20 from both sides of the equation:
x + 20 -20 = 45 - 20
20 - 20 is zero, so this can be simplified to:
x = 25
Thus, we have solved the equation for "x."
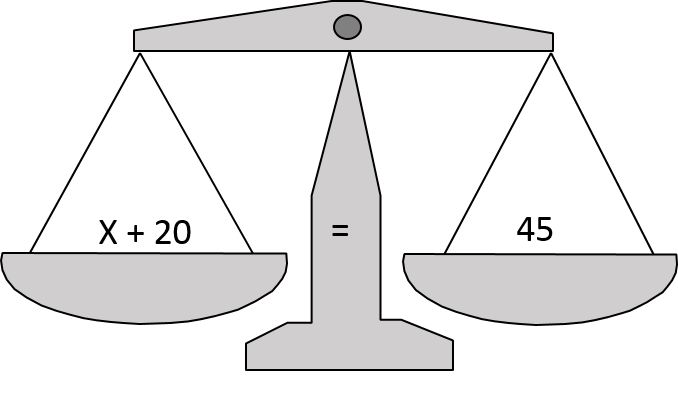
Solving by Addition or Subtraction from Both Sides
Here is another example:
x + 23 = 2x + 45
In this case, the right side has the expression "2x," meaning "2 times x." So, the 2 can be thought of as a "coefficient" indicating what the variable "x" is being multiplied by.
To simplify this equation, we can start by subtracting one "x" from both sides.
x - x + 23 = 2x - x +45
This simplifies to:
23 = 1x +45
Next, we can subtract 45 from both sides in order to get the right side to just have "x" left::
23 - 45 = x + 45 - 45
This simplifies to
-22 = x
So, x = - 22.
Solving by Dividing or Multiplying Both Sides
Suppose 4x = 48
Since we want to find the value of the variable "x," we can just divide both sides of the equation by 4. Remember that as long as we do the same thing to both sides, the equation remains balanced.
Here are the steps:
Divide both sides of the equation by 4.
The 4s on the left side of the equation cancel each other out, leaving just "x".
On the right side of the equation 48/4 =12.
Therefore, x = 12.

Rearranging and Combining Like Terms
Consider the following equation:
2 + 3x + 2x + 8 = 60
The goal is to find the value of "x." The left side of the equation has four terms that are to be added, but the order in which additions occur doesn't matter, so we can rearrange this to the following:
2 + 8 + 3x + 2x = 60
and we can now add the first two terms and combine the last two terms on the left side.
10 + 5x = 60
Next, we can subtract 10 from both sides of the equation.
5x = 50
And then divide both sides of the equation by 5 to solve for x.
x = 10
Distributing a Number
Consider the following equation:
6(2 + 4x) = 60
This indicates that we are to multiply 6 times the quantity inside the parentheses. In the section describing the order in which mathematical operations are performed we saw that the first step is to solve within parentheses, but in this case we have two dissimilar terms within the parentheses. However, we can get around this problem by distributing the multiplier (i.e., 6) over the two terms inside the parentheses as follows:
6(2) + 6(4x) = 60
This can be simplified to:
12 + 24x = 60
Now we can subtract 12 from both sides of the equation:
24x = 48
And finally, divide both sides of the equation by 24:
x = 2


