Effect Measure Modification

In the example looking at the association between physical activity and CHD we noted that the risk ratio was 0.86 in the younger subjects and 0.81 in the older subjects. The similarity indicates that the effect of physical activity on CHD was simiar in both age groups. But what if the risk ratios had been meaningfully different?

Consider the following reports. The American Journal of Family Medicine contained an article describing an unusual neurological syndrome (Reyes syndrome) that developed shortly after a viral illness in 12 subjects. All 12 had taken aspirin during their viral illness, and the author hypothesized that this was a new syndrome of toxicity to aspirin. After the publication of this small case series, the CDC issued a bulletin and asked for reports of similar neurological problems after a viral illness. The responses stimulated a second study based on 64 subjects with the same neurological problems after a viral illness and a comparison group consisting of 17,000 subjects who had had a viral illness but did not have Reyes syndrome. 

Crude Analysis
	Reyes	No Reyes
Aspirin	57	8500
No aspirin	7	8500
Total	64	17000

OR_crude = 8.14

Since most of the cases had been children, the investigators performed a stratified analysis to examine the association between aspirin and Reyes syndrome separately in children and adults. 

	Children				Adults
	Reyes	No Reyes			Reyes	No Reyes
Aspirin	52	2500		Aspirin	5	6000
No aspirin	3	1000		No aspirin	4	7500
Total	55	3500			9	13,500

     OR_children = 6.93 (2.16-22.25)                                     OR_adult = 1.56 (0.42-5.82)

In this case, the association between aspirin use after a febrile illness and development of Reyes syndrome is clearly different in children and adults. This phenomenon is called effect measure modification, but unlike confounding, this is not a mathematical distortion; it is a difference in the response to aspirin in these two age groups. Effect measure modification is not a bias or error, and it is not something that we need to avoid or adjust for. It is just an interesting observation that the measure of association differs across groups.

Effect measure modification simpley means that two or more stratum-specific estimates are different. In other words, the association between an exposure and a disease differs among groups of people. For example, we know that the the relative risk of CHD is higher in males than in females.

Consider another example. Trauma surgeons at Boston City Hospital used their trauma database to look at risk factors for death in automobile drivers who had been injured severely enough to require hospital admission after a collision. Not surprisingly, drivers over the age of 70 had a much higher risk of dying after admission compared to yournger drivers who had been admitted (risk ratio=6.75), even after adjusting to differences in severity of injury. When the data were stratified into unrestrained drivers and those who had worn a seatbelt or had a functioning air bag, the following results were obtained.

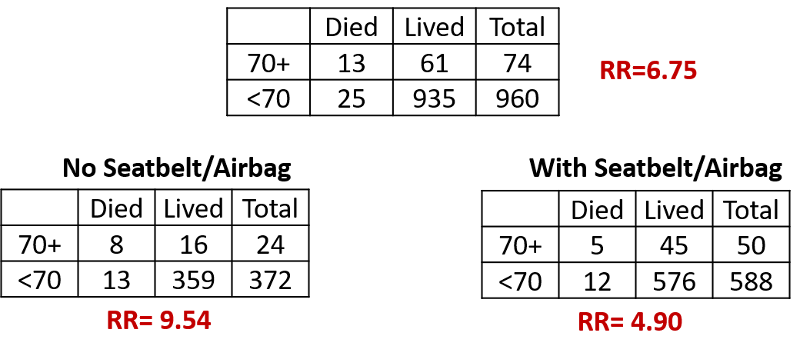
The risk ratio for the association between age and mortality 9.54 in unrestrained drivers and 4.90 in drivers with seatbelts or airbags. Drivers over 70 years of age had a greater risk of dying compared to younger drivers in both subsets, but the association was twice as strong when a seatbelt or airbag was not used.

Rather than obscuring this difference in effect by computing a Mantel-Haenszel pooled estimate, one should report the two effects separately, because it is of scientific interest and to identify subsets of the population that are particularly susceptible (more likely to develop adverse effects).

A Combination of Effect Measure Modification and Confounding

Having said that, be aware that effect measure modification and confounding can both be present. To evaluate that possibility, one can compute a Mantel-Haenszel pooled estimate for the purpose of determining whether confounding was also present. In this case,

OR_MH = 4.48

 We can use this pooled estimate to compute the magnitude of confounding:

 

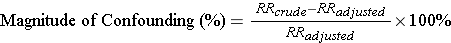
For aspirin use after a febrile illness and Reyes' syndrome:

 

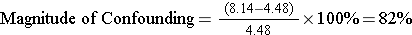
So there was both effective measure modification by age and confounding by age in this study. 

Effective Measure Modification is a Judgment

In this example, there was an obvious difference in the stratum-specific odds ratios, but sometimes there are smaller differences. Unfortunately, the 10% rule for confounding does not apply to determining whether there is effect measure modification. This is a complex area that is beyond the scope of this course. For our purposes, you must make a judgment regarding whether an observed difference in effect is "meaningful" and whether it is plausibly due to a biological phenomenon.

Summary of Stratified Analysis

While the main focus of a study may to evaluate the association between a particular exposure and a particular health outcome, attention must be given to other risk factors that might cause confounding or effect measure modification. Even if they are not of primary interest other risk factors can have several possible effects.

1. Cause neither confounding nor effect modification
2. Cause only confounding
3. Cause only effect modification
4. Cause both confounding and effect modification

 Stratification is a useful tool for

1. Adjusting, i.e., controlling for confounding
2. Detecting effect measure modification (EMM)
3. As a preliminary step prior to multiple variable regression in order to identify risk factors that are potentially causing confounding or EMM

 Steps in Stratified Analysis

1. Calculate crude (unadjusted) measure of association
2. Divide subjects into strata of the confounder
3. Calculate stratum-specific measures of association
4. Calculate adjusted measure of association
5. Determine whether crude measure differs from adjusted measure of association, and by how much (magnitude)
6. Determine whether there is effect measure modification

Some Hypothetical Practice Problems

Test Yourself

A study was conducted to examine the association between smoking and oral cancer in patients who had been previously treated for thyroid cancer. Some of the patients with thyroid cancer had been treated with radiation and some had been treated surgically without radiation. The crude risk ratio for smoking and oral cancer was 2.3. A stratified analysis showed RR=4.8 in those who had been radiated and RR=2.2 in those who had not. The Mantel-Haenszel pooled estimated was RR_MH=2.5. Was there evidence of confounding or effect measure modification?

Answer

 

Test Yourself

A prospective cohort study was conducted to evaluate the association between regular exercise and obesity. The crude incidence rate ratio (IRR) for regular exercisers compared to non-exercisers was 0.78. When stratified by diet (healthy diet versus unhealthy diet), the IRR in healthy eaters was 0.54, and the IRR for unhealthy eaters was 0.85. The Mantel-Haenszel pooled estimate was RR_MH=0.62. Was there evidence of confounding or effect measure modification?

Answer 

 

Test Yourself

Interpret the diet-adjusted incidence rate ratio in the previous question.

Answer 

 

Test Yourself

In the question above on the association between exercise and obesity, interpret the incidence rate ratio for the association of exercise and obesity among healthy eaters.

Answer

return to top | previous page