Adjusting for Confounding in the Analysis
Confounding is a type of bias, because it causes biased estimates of associations. However, confounding is different from selection bias and information bias, because it is caused by an imbalance in other risk factors, and the investigators can adjust for confounding in the analysis phase in order to minimize its effects. This is not true of selection bias or information bias; once they effect a study, there is no way to adjust for them. One can only try to figure out what effect they had on the estimate of effect.
However, if the investigators have collected data from their subjects regarding their status with respect to possible confounding factors, there are methods for computing adjusted measures of association. These are:
- Standardization
- Stratified analysis
- Multiple variable regression analysis
Analytic methods of adjustment attempt to determine how the groups would have compared if they had been comparable with respect to one or more confounding factors. As such, they provide an estimate of effect (association) that is closer to the truth.
Standardization to Control for Confounding
Standardization is a method of computing and comparing adjusted rates of disease that indicate how the groups would have differed if they had had the same distribution of confounders.
To illustrate this we will consider a comparison of mortality rates in Florida and Alaska, two states with very different age distributions. Since older age is clearly a risk factor for death, a crude comparison of mortality rates will be confounded by differences in age.
| Florida | Alaska | |
|---|---|---|
| Total annual deaths | 131,902 | 2,116 |
| Total population | 12,340,000 | 530,000 |
| Crude mortality rate/100,000 | 1,069 | 399 |
The crude mortality rates are clearly different. The crude mortality ratio is 1069/399 = 2.68. Does this mean it is riskier to live in Florida?
Age-Specific Mortality Rates
The table below shows the age-specific mortality rates for Florida and Alaska. Two things are noteworthy. First, despite the difference in overall crude mortality rates, the age-specificmortality rates are quite similar. Second, besides the obvious difference in total population size, the big difference is in the age distribution of the two states. Florida has a larger proportion of older people (who have higher age-specific mortality rates) and Alaska has a greater proportion of younger people (who have lower age-specific mortality rates).
|
|
Florida |
Alaska |
||||
|
Age |
Population |
% of total (weight) |
Rate/100,000 |
Population |
% of total (weight) |
Rate/100,000 |
|
<5 |
850,000 |
7% |
284 |
60,000 |
11% |
274 |
|
5-19 |
2,280,000 |
18% |
57 |
130,000 |
25% |
65 |
|
20-44 |
4,410,000 |
36% |
198 |
240,000 |
45% |
188 |
|
45-64 |
2,600,000 |
21% |
815 |
80,000 |
15% |
629 |
|
>65 |
2,200,000 |
18% |
4,425 |
20,000 |
4% |
4,350 |
|
Totals |
12,340,000 |
100% |
530,000 |
100% |
||
As a result, the comparison of crude rates is unfair because Florida has a much larger proportion of older people who contribute heavily to the overall crude mortality rate in Florida. This comparison is clearly confounded by differences in age.
In essence, the crude mortality rate is a weighted average of the age-specific mortality rates for which the "weight" is the proportion of each population in a given age category. For example, if I multiply the proportion in each age category for Florida by the corresponding age-specific rate and add these up, I will get the crude mortality rate for Florida:
0.07(284) + 0.18(57) + 0.36(198) + 0.21(815) + 0.18(4425) = 1069
So, the crude rates are summary rates that indicate the weighted average of the age-specific rates.
The key question here is "How would the overall mortality rates have compared if the two populations had had the same age distribution?" If we could do this, we could compute an overall mortality rate that was unconfounded and more accurately reflected the similarity that we see in the age-specific rates in the two populations.
We can actually answer this question by using each state's observed age-specific rates and a single age distribution, i.e., a uniform set of "weights," meaning the proportion in each age category. By doing this, we can calculate hypothetical summary rates that are unconfounded by differences in age distribution, because we are applying the same age distribution to each state's observed age-specific rates. By doing this we can calculate adjusted overall summary rates that are no longer confounded by differences in age distribution.
To illustrate we will arbitrarily use the distribution of the United States population in 1988 as the standard set of weights. (We could use any other year, and it won't matter as long as we apply the standard set to both populations).
The age-distribution in the US in 1988 was:
| Age Category | Percent of Total Population |
|---|---|
| <5 | 7% |
| 5-19 | 22% |
| 20-44 | 40% |
| 45-64 | 19% |
| >65 | 12% |
Now let's use these weights to calculate age-adjusted rates, first for Florida, and then for Alaska.
Mortality Rate FL.adjusted = 0.07(284) + 0.22(57) + 0.40(198) + 0.19(815) + 0.12(4425) = 797/100,000
Mortality Rate Alaska.adjusted = 0.07(274) + 0.22(65) + 0.40(188) + 0.19(629) + 0.12(4350) = 750/100,000
These summary rates are hypothetical, but we can use them to provide a comparison of mortality rates that is not confounded by age.
Standardized Mortality Rate Ratio (SMR) = 797/750 = 1.06
Recall that the mortality rate ratio was 2.68, but now the standardized mortality rate ratio is 1.06, very close to the null value of 1.
Standardization is frequently used to generate "age-adjusted" rates not only for mortality, but for many other health outcomes in publications from CDC and in publications like Healthy People 2020. The image below shows heart disease deaths for black and white males and females in Massachusetts from 1970 to 1993. The footnote at the bottom says, "Rates are age-adjusted by the direct method using the 1940 U.S. population as a standard."

Having computed age-adjusted CHD death rates for each of these four sex and gender groups at multiple points in time, we get a clear picture of differences among the four groups and trends over time, and these comparisons are not distorted by the differences in age distribution among the groups over time. We can see clearly that CHD death rates have fallen in all four groups, but there are persistent large differences between males and females, even though the gap has narrowed somewhat. In addition, white females continue to have slightly lower CHD mortality rates than black femailes, and white males have slightly lower rates than black males.
An Operational Way to Identify a Confounding Factor
A useful way to identify confounding is to calculate the crude (unadjusted) measure of association and then compute the measure of association again after adjusting for a possible confounding factor, as we did above. If the two differ, it suggests that the factor we adjusted for was a confounder. But how big a difference must there be to conclude that there was confounding?
The 10% Rule for Confounding
Most epidemiologists use a 10% difference as a "rule of thumb" for identifying the presence of confounding. The magnitude of confounding is the percent difference between the crude and adjusted measures of association, calculated as follows (for either a risk ratio or an odds ratio):

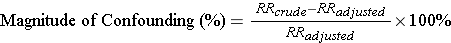
If the % difference is 10% or greater, we conclude that there was confounding. If it is <10%, we conclude that there was little, if any, confounding.
For mortality rate ratios in Florida and Alaska:

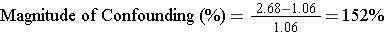
Since 152% is much greater than 10%, the comparison of mortality rates was clearly confounded by differences in age distribution
Finally, note that the 10% rule of thumb for confounding is not rigid. Epidemiologists sometimes adjust for factors when the percent difference is less than 10%.


