What Is Confounding?
Suppose we want to assess the strength of association between physical activity and coronary heart disease (CHD). For simplicity let's assume that we have just two exposure groups:
- Active
- Sedentary
We follow the subjects for ten years and find that the risk ratio for developing CHD in the active group compared to the sedentary group is 0.5, suggesting that those who are physically active have 0.5 times the risk of developing coronary heart disease compared to those who are sedentary. But is this an accurate assessment of the effect of physical activity on risk of CHD?
Older people tend to be less physically active then younger people, and age is clearly a risk factor for coronary heart disease. If the sedentary group is older, how do we separate the impact of physical activity (which we are mainly interested in) from age (which is just another risk factor that confuses things)?
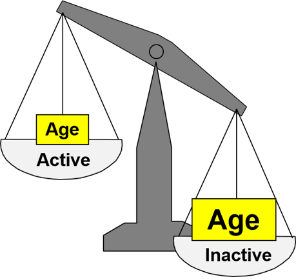
The unequal distribution of age (another risk factor) exaggerates the apparent effect of inactivity. Age differences between active and sedentary people confound the association between activity and CHD. Confounding is the distortion of a measure of association that occurs when other risk factors for the outcome are unevenly distributed between the groups being compared
If the age distribution had been similar in the active and inactive groups, we might have found that the active group had a lower risk of CHD, but the apparent benefit of exercise would have not been as great because age differences were no longer distorting the comparison.
Conditions for Confounding to Occur
Another exposure can cause confounding if three conditions are met:
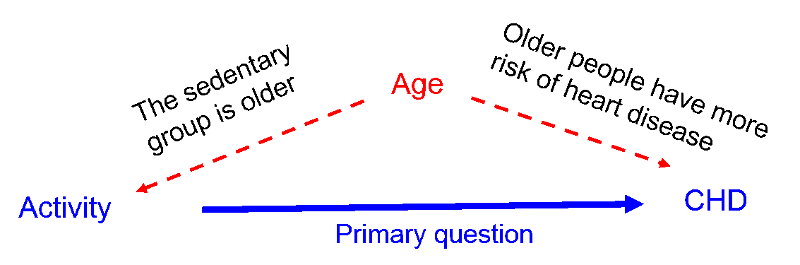
1) The additional exposure is an independent risk factor for the outcome under study, i.e., the confounding factor is associated with the outcome. In this example, older age is an independent risk factor for CHD.
2) The distribution of the confounding factor differs among the exposure groups, i.e., it is associated with the exposure. In this example, the sedentary group has a greater proportion of older people.
These first two conditions might be depicted by the figure below in which the primary question of interest is the association between activity and CHD, but differences in age distort the measure of association because older people are less active and older people have an inherently greater risk of CHD that is independent of their activity level.
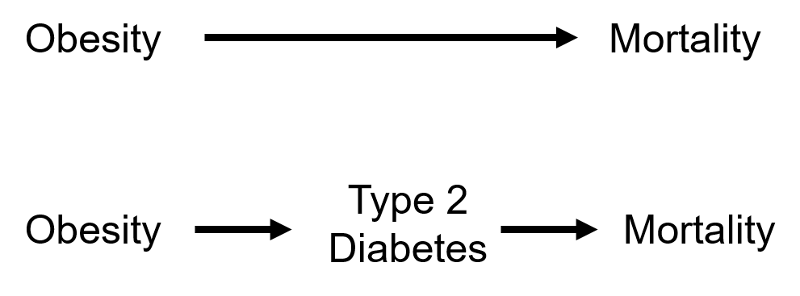
3) A confounding factor cannot be an intermediary factor in the causal pathway between the exposure and the outcome. For example, obesity is a cause of type 2 diabetes, and type 2 diabetes is a cause of coronary heart disease. Given this sequence of events in the causal chain, type 2 diabetes would not be considered a confounding factor for the association between obesity and coronary artery disease, because it is the mechanism by which obesity leads to coronary heart disease.
Effects of Confounding
Later in this module we will discuss methods for adjusting for the distortion caused by confounding. A crude measure of association is one that has not yet been adjusted for confounding factors, while an adjusted measure of association is one that has been adjusted to minimize confounding and provides an estimate that is closer to the true value.
Confounding can bias the primary measure of association toward the null, causing an underestimate of the association. This is referred to as negative confounding. As illustrated below, if the true (adjusted) risk ratio or odds ratio was 3 and the crude, i.e., confounded estimate was OR or RR=2, that would be an underestimate. Similarly, if the true ratio was 0.25 (a preventive effect) and the crude estimate was 0.5, that would be an underestimate of the preventive effective.
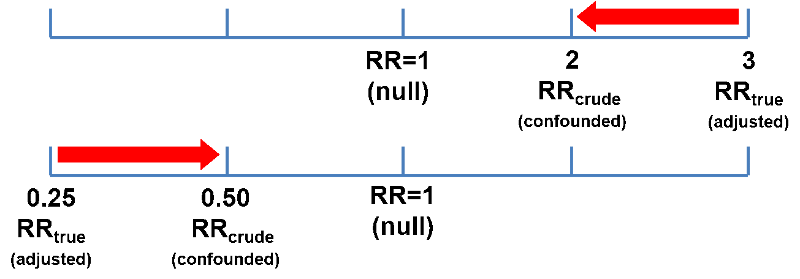
Confounding can also bias the measure of association away from the null, causing an overestimate of the association. This is called positive confounding. If the true odds ratio was 2 and the crude estimate was 3, that would represent an overestimate of the risk. And if the true odds ratio was 0.5 and the crude estimate was 0.25, that would also be bias away from the null and an overestimate of the preventive effect.
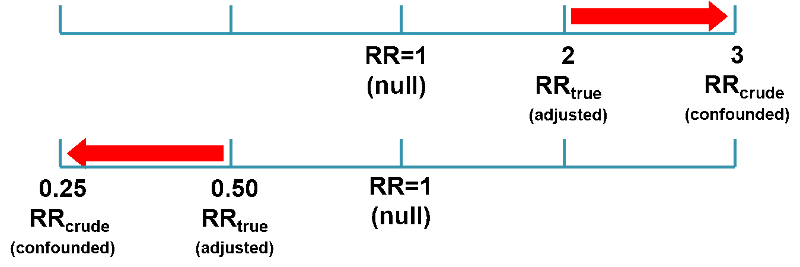
So, negative and positive confounding are distinguished not by whether it causes the measure of association to appear smaller or larger than the true value, but by whether it causes the estimated measure of association to move toward the null (negative) or away from the null (positive).


