Measuring Association in Case-Control Studies
All the examples above were for cohort studies or clinical trials in which we compared either cumulative incidence or incidence rates
or incidence rates among two or more exposure groups. However, in a true case-control study we don't measure and compare incidence. There is no "follow-up" period in case-control studies.
among two or more exposure groups. However, in a true case-control study we don't measure and compare incidence. There is no "follow-up" period in case-control studies.
In the module on Overview of Analytic Studies we considered a rare disease in a source population that looked like this:
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
7 |
1,000 |
1,007 |
|
Non-exposed |
6 |
5,634 |
5,640 |
This view of the population is hypothetical because it shows us the exposure status of all subjects in the population. We therefore know the total number of exposed and non-exposed people (in the "Total" column). If we know all this, we could compute the incidence in each group (the incidence in the exposed individuals would be 7/1,007 = 0.70%, and the incidence in the non-exposed individuals would be 6/5,640 = 0.11%), and we could compute the risk ratio (RR = 6.53). All of our computations involved the "Diseased" column and the "Total" column.
Another way of looking at this association is to consider that the "Diseased" column tells us the relative exposure status in people who developed the outcome (7/6 = 1.16667), and the "Total" column tells us the relative exposure status of the entire source population (1,007/5,640 = 0.1785). The ratio of these two distributions (7/6)/(1,007/5,640) = 6.53, because it is just an algebraic rearrangement of the same four numbers we used to compute the cumulative incidences and the risk ratio. Note also that the relative exposure distribution in the "Total" population is very similar the relative exposure distribution in the "Non-diseased" portion of the source population, because the disease is rare. Consequently, in order to estimate the risk ratio we could use the relative distribution of exposure in the "Non-diseased" subjects - OR, to be more efficient, we could just take a sample of non-diseased subjects in order to estimate their exposure distribution. We could for example, just sample 1% of the non-diseased people and I then determine their exposure status. The data might look something like this:
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
7 |
10 |
unknown |
|
Non-exposed |
6 |
56 |
unknown |
The Odds Ratio
The relative exposure distributions (7/6) and (10/56) are really odds, i.e. the odds of exposure among cases and non-diseased controls. If we compute the ratio of these two odds we would get:

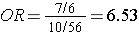
i.e., almost identical to the risk ratio we calculated when we had all the information for the source group. Note that we would get the same answer if we computed the odds ratio by dividing the odds of disease in the exposed (7/10) by the the odds of disease in the non-exposed group (6/56).

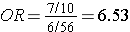
because this expression is just an algebraic rearrangement of the previous equation.
Odds Ratio as an Estimate of Risk Ratio
Provided that the disease is uncommon (say <10%), this sampling approach gives an odds ratio that is a reasonably good estimate of the risk ratio. Very rare outcomes (e.g., in the tables above) will give odds ratios that are extremely close to what the risk ratio would be. However, as the outcomes of interest become more common, the odds ratio gives estimates that are increasing more extreme than the risk ratio would have been. By more extreme, I mean that odds ratios that are greater than 1 will be larger than the corresponding risk ratio, and odds ratios that are less than 1 will be smaller than the corresponding risk ratio.
The figure below depict shows that when the outcome is more common (e.g., >10%), the odds ratio exaggerates the estimated strength of association.
|
|
Diseased |
Non-Diseased |
Total |
Cumulative Incidence |
|
Exposed |
60 |
108 |
168 |
60/(60+108) = 35.7% |
|
Non-Exposed |
45 |
341 |
386 |
45/(45+341) = 11.7% |

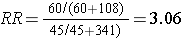

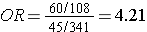
The interactive feature below allows you to simultaneously compute both the risk ratio and the odds ratio in a hypothetical cohort study. In general, the odds ratio will be close in value to the risk ratio when the outcome of interest is rare, but the odds ratio will tend to become more extreme than the risk ratio as the outcome becomes increasingly common.You can use this widget to observe how the odds and probabilities change as you make the outcome more common. For example, enter numbers in the cells that would be consistent with a rare outcome and compare the OR and the RR. Then increase the frequency of the outcome by doubling, quadrupling, etc. the number of events in the first column without changing the second column.
|
Key Concept: Remember that in a cohort study you can calculate either a risk ratio or an odds ratio, but In a case-control study: you can only calculate an odds ratio.
|
Incidence is Unknown in a Case-Control Study
In a cohort type study, one can calculate the incidence in each group, the risk ratio, the risk difference, and the attributable fraction. In addition, one can also calculate an odds ratio in a cohort study, as we did in the two examples immediately above. In contrast, in a case-control study one can only calculate the odds ratio, i.e. an estimate of relative effect size, because one cannot calculate incidence. Consider once again the table that we used above to illustrate calculation of the odds ratio.
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
7 |
10 |
unknown |
|
Non-exposed |
6 |
56 |
unknown |
In this table the total number of exposed and non-exposed subjects is not known, because sampling was done using a case-control design. One might find many or all of the cases in a source population, particularly if it is a reportable disease. In this example, the investigators found all thirteen cases, but then they just sampled 66 non-diseased people in order to estimate the exposure distribution in the source population. When a case-control approach is used for sampling, we don't know how many exposed people it took to generate the 7 cases in the first row, and we don't know how many non-exposed persons were needed to generate the 6 cases in the second row. The information from non-diseased controls allow us to estimate the exposure distribution in the source population, .we don't know the denominators ("Totals") for either exposure group.
Attributable Proportion Among the Exposed in Case-Control Studies
While it is generally not possible to calculate the absolute risk of disease (incidence) in a case control study, it is possible to estimate the attributable proportion among the exposed (AR%). It was noted earlier in the module that the attributable proportion among the exposed in cohort type studies can also be calculated from the formula:

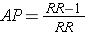
Since the OR is an estimate of RR, then by analogy the attributable proportion among the exposed can be estimated in a case-control study from the formula:

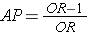
This can also be expressed as a percentage by multiplying by 100.
Population Attributable Fraction (PAF) in a Case-Control Study
Finally, since it is possible to estimate the attributable proportion in the exposed in a case-control study, it is also possible to compute the population attributable proportion in an analogous way to the computation in cohort type studies, i.e.,

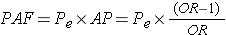
where Pe is the proportion of cases that have the exposure.