
Measures of Association
We search for the determinants of health outcomes, first, by relying on descriptive epidemiology to generate hypotheses about associations between exposures and outcomes, and, second, by employing analytical epidemiology to more rigorously assess hypotheses by drawing samples of people and comparing groups to determine whether health outcomes differ based on exposure status. If individuals with a given exposure are found to have a greater probability of developing a particular outcome, it suggests an association, and, conversely, if the groups have the same probability of developing the outcome regardless of their exposure status, it suggests that particular exposure is not associated with a greater risk of disease. In either event one must then consider whether the findings were misleading because of sampling error, bias, or confounding (the issue of validity is one that we will address later); in other words, we must consider alternative explanations that might invalidate our conclusions. In this module we will focus on methods for comparing groups and how to interpret the findings.
After successfully completing this section, the student will be able to:

In a previous module we saw that we can measure disease frequency (cumulative incidence, incidence rate, or prevalence) by identifying the number of cases in the numerator and the population (people or person-time) in the denominator. Knowing the level of disease frequency in a single group, however, does not tell us whether membership in that group increases, decreases, or has no effect on risk. We can measure the cumulative incidence of twin (or higher multiple) births among women who use fertility treatment but we can't draw any preliminary conclusion without knowing the incidence of similar births among women who didn't use such treatment. Thus, identifying the causes of disease in epidemiology inherently involves comparison between groups of people who differ by exposure. This difference could be qualitative (yes/no), such as whether one did or did not consume a certain food at a restaurant on a specific evening, or quantitative (higher/lower), such as differences in the amount of carbohydrates consumed in one's diet. By measuring and comparing the incidence of the outcome of interest in two or more groups categorized by extent of exposure, we can begin to assess whether there is an association between exposure and outcome.
Because many potential causes fit more into the quantitative rather than qualitative category, a more general way to conceptualize comparisons is to think of the category of interest (the category hypothesized to be associated with disease) as the "index" category and the category that serves as the comparison as the "reference" category. You will often see this usage.
The format in which the data for different groups can be summarized is very simple and is the same regardless of the measure of disease frequency. A generic template is shown in the figure: exposure status (in this case, yes/no) is indicated in rows, and the outcome status for each exposure category is shown in the columns.
Consider the following example regarding the management of Hodgkin lymphoma, a cancer of the lymphatic system. Years ago when a patient was diagnosed with Hodgkin Disease, they would frequently undergo a surgical procedure called a "staging laparotomy." The purpose of the staging laparotomy was to determine the extent to which the cancer had spread, because this was important information for determining the patient's prognosis and optimizing treatment. At times, the surgeons performing this procedure would also remove the patient's appendix, not because it was inflamed; it was done "incidentally" in order to ensure that the patient never had to worry about getting appendicitis. However, performing an appendectomy requires transecting it, and this has the potential to contaminate the abdomen and the wound edges with bacteria normally contained inside the appendix. Some surgeons felt that doing this "incidental appendectomy" did the patient a favor by ensuring that they would never get appendicitis, but others felt that it meant unnecessarily increasing the patient's risk of getting a post-operative wound infection by spreading around the bacteria that was once inside the appendix. To address this, the surgeons at a large hospital performed a retrospective cohort study. They began by going through the hospital's medical records to identify all subjects who had had a "staging laparotomy performed for Hodgkin." They then reviewed the medical record and looked at the operative report to determine whether the patient had an incidental appendectomy or not. They then reviewed the progress notes, the laboratory reports, the nurses notes, and the discharge summary to determine whether the patient had developed a wound infection during the week after surgery. The investigators reviewed the records of 210 patients who had undergone the staging procedure and found that 131 had also had an incidental appendectomy, while the other 79 had not. The data from that study are summarized in the table below. The numbers in the second and third columns indicate the number of subjects who did or did not develop a post-operative wound infection among those who had the incidental appendectomy (in the "Yes" row) and those who did not have the incidental appendectomy (in the "No" row). For example, the upper left cell indicates that seven of the subjects who had an incidental appendectomy (the exposure of interest) subsequently developed a wound infection. The upper right cell indicates that the other 124 subjects who had an incidental appendectomy did NOT develop a wound infection.
|
Had Incidental Appendectomy? |
Wound Infection |
No Wound Infection |
Total |
|
Yes |
7 |
124 |
131 |
|
No |
1 |
78 |
79 |
.


There is no fixed convention for setting up a 2x2 (also known as contingency) table. However, when you use these tables to compute measures of association there is a distinct advantage to setting them up the same way all the time. If you don't, you can get confused when calculating measures of association. While you should set up your tables consistently, be aware that others may organize their tables differently, so be careful. I always put the exposure groups in rows with the row labels to the left, and I put the exposed (or most exposed) group on the top row. Outcome status is listed in the vertical columns; those with the outcome are listed in the left column.
Note also that contingency tables can accommodate more than two exposure groups just adding additional rows as illustrated on page 4 of this module. .
The fundamental methods for comparing the frequency of disease (or health events in general) are to:
Measures of disease frequency can be compared by calculating their ratio. Common terms to describe these ratios are
Frequently, the term "relative risk" is used to encompass all of these. These relative measures give an indication of the "strength of association."
For the study examining wound infections after incidental appendectomy, the risk of wound infection in each exposure group is estimated from the cumulative incidence. The relative risk (or risk ratio) is an intuitive way to compare the risks for the two groups. Simply divide the cumulative incidence in exposed group by the cumulative incidence in the unexposed group:
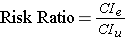
where CIe is the cumulative incidence in the 'exposed' group and CIu is the cumulative incidence in the 'unexposed' group.
The table below shows how the risk ratio was calculated in the study examining the risk of wound infections when an incidental appendectomy was done during a staging laparotomy for Hodgkin disease.
|
Had Incidental Appendectomy? |
Wound Infection |
No Wound Infection |
Total |
Cumulative Incidence |
|
Yes |
7 |
124 |
131 |
7/131 = 5.34% |
|
No |
1 |
78 |
79 |
1/79 = 1.27% |
Risk Ratio = 5.34/1.27 = 4.2
Organization of the information in a contingency table facilitates analysis and interpretation. The cumulative incidence is an estimate of risk. Incidental appendectomies were performed in a total of 131 patients, and seven of these developed post-operative wound infections, so the cumulative incidence was 7 divided by 131, or 5.34%. We can similarly calculate the cumulative incidence in the patients who did not have an incidental appendectomy, which was 1 divided by 79 or 1.27%. So, the risk ratio is 5.34/1.27 or 4.2.
Interpretation:
In this study patients who underwent incidental appendectomy had 4.2 times the risk of post-operative wound infection compared to patients who did not undergo incidental appendectomy.
It is also possible for the risk ratio to be less than 1; this would suggest that the exposure being considered is associated with a reduction in risk. In 1982 The Physicians' Health Study (a randomized clinical trial) was begun in order to test whether low-dose aspirin was beneficial in reducing myocardial infarctions (heart attacks). The study population consisted of over 22,000 male physicians who were randomly assigned to either low-dose aspirin or a placebo (an identical looking pill that was inert). They followed these physicians for about five years. Some of the data is summarized in the 2x2 table shown below.
|
Treatment |
Myocardial Infarction |
No Infarction |
Total |
Cumulative Incidence |
|
Aspirin |
139 |
10,898 |
11,037 |
139/11,037 = 0.0126 |
|
Placebo |
239 |
10,795 |
11,034 |
239/11,034 = 0.0217 |
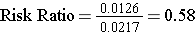
Note that the "exposure" of interest was low-dose aspirin, and the aspirin group is summarized in the top row. The group assigned to take aspirin had an incidence of 1.26%, while the placebo (unexposed) group had an incidence of about 2.17%. The cumulative incidence in the aspirin group was divided by the cumulative incidence in the placebo group, and RR= 0.58. An appropriate interpretation of this would be:
Those who take low dose aspirin regularly have 0.58 times the risk of myocardial infarction compared to those who do not take aspirin.
Note also that the unexposed (comparison, reference) group must be specified. For example, if we simply said, "Those who take low dose aspirin regularly have 0.58 times the risk of myocardial infarction", the question is "compared to what?" Is it those who didn't take any aspirin, those who took low-dose aspirin but used it irregularly, those who took high dose aspirin, those who took acetaminophen...?
In general:
An alternative way to look at and interpret these comparisons would be to compute the percent relative effect (the percent change in the exposed group). In essence, we regard the unexposed group as having 100% of the risk and express the exposed group relative to that. For example,
When RR > 1
For the wound infection study, the group that had the incidental appendectomy had a 320% increase in risk over and above the risk in the unexposed group (100%). When RR > 1,
% increase = (RR - 1) x 100, e.g. (4.2 - 1) x 100 = 320% increase in risk.
Interpretation: Those who had the incidental appendectomy had a 320% increase in risk of getting a post-operative wound infection.
When RR < 1
For the aspirin study, the men on low-dose aspirin had a 43% reduction in risk. When RR < 1,
% decrease = (1 - RR) x 100, e.g. (1 - 0.57) x 100 = 43% decrease in risk
Interpretation: Those who took low-dose aspirin had a 43% reduction in risk of myocardial infarction compared to those who did not take aspirin.
 Pitfalls: Note that in the interpretation of RR both the appendectomy study (in which the RR > 1), and the aspirin trial (in which RR < 1) used the expression "times the risk." To be precise, it is not correct to say that those who had an incidental appendectomy had 4.2 times more risk (wrong) or 4.2 times greater risk (wrong). In fact, those with the incidental appendectomy had a 320% increase in risk. Conversely, in the aspirin study it is not correct to say that those on aspirin had 0.57 times less risk (wrong). In fact, they had 43% less risk.
Pitfalls: Note that in the interpretation of RR both the appendectomy study (in which the RR > 1), and the aspirin trial (in which RR < 1) used the expression "times the risk." To be precise, it is not correct to say that those who had an incidental appendectomy had 4.2 times more risk (wrong) or 4.2 times greater risk (wrong). In fact, those with the incidental appendectomy had a 320% increase in risk. Conversely, in the aspirin study it is not correct to say that those on aspirin had 0.57 times less risk (wrong). In fact, they had 43% less risk.
CORRECT:
INCORRECT:
|
Key Concept How to Interpret Risk Ratios: Since the relative risk is a simple ratio, errors tend to occur when the terms "more" or "less" are used. Because it is a ratio and expresses how many times more probable the outcome is in the exposed group, the simplest solution is to incorporate the words "times the risk" or "times as high as" in your interpretation. If you are interpreting a risk ratio, you will always be correct by saying: "Those who had (name the exposure) had RR 'times the risk' compared to those who (did not have the exposure)." Or "The risk of (name the disease) among those who (name the exposure) was RR 'times as high as' the risk of (name the disease) among those who did not (name the exposure)."
|




Question: Does one need to specify the time units for a risk ratio? (Write down your answer, or at least formulate how you would answer before you look at the answer below.)
Answer
Rate ratios are closely related to risk ratios, but they are computed as the ratio of the incidence rate in an exposed group divided by the incidence rate in an unexposed (or less exposed) comparison group.
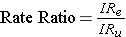
Consider an example from The Nurses' Health Study. This prospective cohort study was used to investigate the effects of hormone replacement therapy (HRT) on coronary artery disease in post-menopausal women. The investigators calculated the incidence rate of coronary artery disease in post-menopausal women who had been taking HRT and compared it to the incidence rate in post-menopausal women who had not taken HRT. The findings are summarized in this table:
|
Post-menopausal Hormone Use |
# with Coronary Artery Disease |
Person-Years of Disease-free Follow-up |
|
Yes |
30 |
54,308.7 |
|
No |
60 |
51,477.5 |
So, the rate ratio was 0.47.
Interpretation: Women who used postmenopausal hormones had 0.47 times the rate of coronary artery disease compared to women who did not use postmenopausal hormones.
(Rate ratios are often interpreted as if they were risk ratios, e.g., post-menopausal women using HRT had 0.47 times the risk of CAD compared to women not using HRT, but it is more precise to refer to the ratio of rates rather than risk.)


Some cohort studies and clinical trials compare the risk of disease or other outcomes among three or more exposure groups. In this situation, results can be summarized in a table with multiple rows to accommodate the multiple exposure groups. This is a logical extension of the basic "2 x 2" table and is sometimes referred to as an "r x c" table (row and columns).
Use of a Reference Group with Risk Ratios
The table below summarizes a study examining the association between exposure to magnetic fields, e.g., from high tension wires, and the risk of leukemia. In this study there are no unexposed subjects, but we can classify them as having low, medium, and high exposure. To compute the risk ratios , it is logical to use the least exposed group as a "reference group" against which we can compare the other two exposure (or "index") groups. Note that in this example the investigators calculated and compared cumulative incidence.
|
Magnetic Field Exposure |
Leukemia |
No Leukemia |
Total |
Cumulative Incidence |
|
High |
30 |
644 |
674 |
30 / 674 = 0.0445 |
|
Medium |
61 |
1,408 |
1,469 |
61 / 1,469 = 0.0415 |
|
Low |
2,264 |
65,160 |
67,424 |
2,264 / 67,424 = 0.0336 |
The group with the lowest exposure had a cumulative incidence of 0.0336 or 33.6 per 1000 over the period of observation, while the medium exposure group had 41.5 per 1000 and the highest exposure group had 44.5 per 1000.
Interpretation:
Compared to children exposed to low magnetic field levels, those exposed to medium levels have 1.23 times the risk of leukemia (a 23% increase in risk), and those exposed to high levels have 1.33 times the risk (a 33% increase in risk).
Use of a Reference Group with Rate Ratios
When The Nurse's Health Study looked at the association between obesity & heart disease, they compared the risk of heart attacks in five categories of body mass index. They used the leanest group of women as a reference group against which they compared each of the other four groups. Note that in the table below, the exposure groups form the rows while the columns indicate the number of outcome events, the person-years of observation, and the incidence rate for each exposure group. The last column shows the rate ratio for each group, using the leanest women as the reference group.
|
Body Mass Index (BMI) |
Non-fatal Myocardial Infarctions |
Person-Years of Event-free Observation |
Incidence Rate per 100,000 P-Yrs |
Rate Ratio |
|
<21 |
41 |
177,356 |
23.1 |
- |
|
21-23 |
57 |
194,243 |
29.3 |
1.3 |
|
23-25 |
56 |
155,717 |
36.0 |
1.6 |
|
25-29 |
67 |
148,541 |
45.1 |
2.0 |
|
>29 |
85 |
99,573 |
85.4 |
3.7 |
It is apparent that there is a progressive increase in risk as BMI goes up, and women in the highest BMI category had 3.7 times the rate of myocardial infarction compared to the leanest women.
Instead of comparing two measures of disease frequency by calculating their ratio, one can compare them in terms of their absolute difference. The risk difference is calculated by subtracting the cumulative incidence in the unexposed group (or least exposed group) from the cumulative incidence in the group with the exposure.
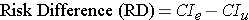
where (CIe) = cumulative incidence among the exposed subjects, and (CIu) is the cumulative incidence among unexposed subjects.
The risk difference focuses on absolute effect of the risk factor, or the excess risk of disease in those who have the factor compared with those who don't. Recall that in the wound infection study, the cumulative incidence of infection was 5.3% in the incidental appendectomy group, and only 1.3% in the group without appendectomies. The risk ratio was 4.2, but we can also compute the absolute difference, which is 5.3/100 - 1.3/100 = 4 per 100 excess wound infections among those who had the incidental appendectomy. CIu provides an estimate of the baseline risk (i.e., in the absence of the exposure), and the exposure factor imposes an additional (excess) risk on top of that.
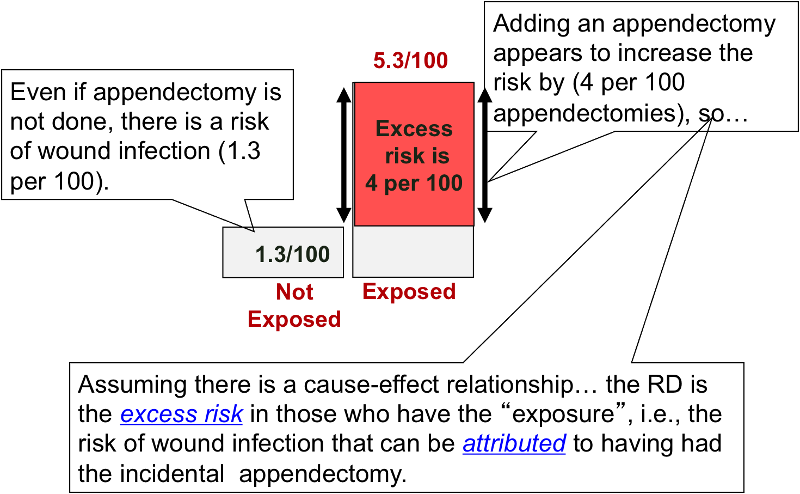
An older term for the risk difference is "attributable risk," that is the excess risk than can be attributed to having had the exposure. However, many discourage the use of this terminology because it presumes a causal relationship between the exposure and the outcome.
Note also that any measure of association in a single study, whether a ratio or difference, should be considered one estimate of the true causal relationship.
|
Tips For Interpreting Risk Difference
Example: CI with appendectomy = 5.3% = 53/1000 CI without appendectomy = 1.3% = 13/1000 Risk Difference = 40/1000= 4/100 Interpretation: Subjects who had an incidental appendectomy had 4 additional cases of wound infection per 100 people compared to subjects who did not have an incidental appendectomy. What is wrong with the following? "Subjects who had an incidental appendectomy had 4% more cases of wound infection compared to subjects who did not have an incidental appendectomy." Since percentages are also used to express excess risk relative risk, this statement could lead to confusion. Does it mean that the RR was 1.04, or that there were an additional 4 cases per 100 people in the exposed group compared to those in the unexposed group?
Example: "There were 4 excess wound infections per 100 subjects in the group that had incidental appendectomies, compared to the group without incidental appendectomy."
Example: "In the group that failed to adhere closely to the Mediterranean diet there were 120 excess deaths per 1,000 men during the two year period of observation compared to the group that did adhere to the Mediterranean diet."
|
Analogous to the risk difference, the rate difference is calculated by subtracting the incidence rate in the unexposed group (or least exposed group) from the incidence rate in the group with the exposure.
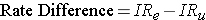
where (IRe) = incidence rate among the exposed subjects, and (IRu) is the incidence rate among unexposed subjects.
When we compute a rate ratio, the units of person-time in the denominator cancel out because of division. However, a rate difference is based on subtraction of incidence rates, so the units are retained. In the Nurses' Health Study, the difference between highest and lowest weight categories was about 62.3 cases per 100,000 person-years (see figure to the right). If you followed another 100,000 women with BMI's >29 for one year, you would expect about 85 of them to have a non-fatal MI, and we could attribute about 62 of these to their obesity. Conversely, if you got these 100,000 women to lose enough weight to get them down into the leanest category, you might expect to prevent about 62 non-fatal MIs.
Note that interpretation of risk difference in this way is based on the assumption that there is both a valid association (not due to random error, bias or confounding) and the assumption that there is a cause-effect relationship between the exposure and the disease.
Interpretation: Nurses who had a BMI>29 had 62.3 additional cases of non-fatal myocardial infarction per 100,000 person-years compared to nurses who had a BMI<21.
Tip #4: Because person-year units are retained in the denominator, the rate difference, can never be reported as a percentage.


Relative risk comparisons and risk differences provide two different perspectives on the same information.
Example:
How effective is fecal blood testing as a screening test for colorectal cancer?
A study found that people over age 40 who were screened had a 33% reduction in death (i.e. RR = 0.67) from colorectal cancer compared to people who were not screened; in other words those who were screened had 0.67 times the risk of death from colorectal cancer. However, the incidence of death in the screened group was 6 per 1,000 people, and the incidence of death in the unscreened group was 9 per 1,000. In other words, screening may have saved 3 lives per 1,000 people screened. A 33% reduction sounds like a lot, but when you consider that the risk difference was perhaps only 3 per 1,000 screened, it doesn't sound like as much of a benefit.


(Also called the Attributable Fraction or the Attributable Risk %)
The same information allows you to calculate the proportion of disease in the exposed group that can be attributed to the exposure. This can also be looked at as the proportion of disease in the exposed group that could be prevented by eliminating the risk factor. It is calculated by taking the risk difference, dividing it by the incidence in the exposed group, and then multiplying it by 100 to convert it into a percentage.

Attributable proportion can also be expressed as a percent, i.e., the percentage of disease in the exposed group that can be attributed to the exposure (sometimes called the attributable risk %). The calculation is the same, except you multiply x 100 to convert the proportion into a %.
Example:
In the wound infection study, the incidence in the exposed group was 5.3 per 100. Of this, 4 per 100 could be attributed to having had the incidental appendectomy (the other 1.3 per 100 was the "inherent risk" of the staging laparotomy). Therefore,
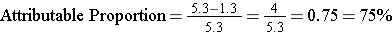
so 75% of the wound infections in the group that had the incidental appendectomy could be attributed to having had the appendectomy.

Consider the following table [adapted from Rothman: Epidemiology - An Introduction], and compute the attributable proportion in the exposed group.Do the calculation following the example above before you look at the answer.
|
Exposure Status |
Diseased |
No Disease |
Population |
|
Cumulative Incidence (Risk) |
|---|---|---|---|---|---|
|
Exposed |
500 |
9,500 |
10,000 |
|
0.050 |
|
Not Exposed |
900 |
89,100 |
90,000 |
|
0.010 |
|
Column Totals |
1,400 |
98,600 |
100,000 |
|
0.014 |
ANSWER
Sometimes you will not have the actual cumulative incidence or incidence rates available, but will know the risk or rate ratio. In that case, it is very helpful to know this alternative formula for calculating the attributable proportion:
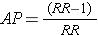
For example, the RR in the laparotomy study was 4.2. Plugging this value into the above formula gives (4.2 - 1)/4.2 = 3.2/4.2 = 76%, which differs only by rounding error from the result obtained using the other formula.

Question: Is it possible to compute the attributable proportion in the exposed from incidence rates?
Answer
The attributable proportion makes sense when one is dealing with an exposure that increases the risk of a disease. The flip side of this is the situation when one is dealing with an exposure that reduces the risk of disease. In this case, it makes more sense to think about the preventive fraction (or proportion).
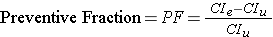
This is similar to the attributable proportion, except that the risk difference (i.e., the risk reduction) is divided by the cumulative incidence in the unexposed group. This can also be expressed as a percent, i.e., the percentage of disease reduction in the exposed group that can be attributed to the beneficial exposure.
Example:
In 1945 Newburgh, New York and two other communities began fluoridating their public water supply. As a result, the incidence of dental caries was 14.8% versus 21.3% in nearby Kingston, NY, which was non-fluoridated. Thus, the preventive fraction was (21.3-14.8)/21.3 = 30.5%, indicating that about 30% of the caries that would have occurred in Newburgh were prevented by fluoridation.
(Also called the Population Attributable Proportion or Attributable Proportion Among the Total Population)
One can also compute the proportion or percentage of cases in the entire study population that can be attributed to the exposure. In the problem above we computed the attributable fraction for the exposed group, but what is the attributable fraction for the entire population?
Consider the example on the previous page, which is summarized by this table:
|
Exposure Status |
Diseased |
No Disease |
Population |
|
Cumulative Incidence (Risk) |
|---|---|---|---|---|---|
|
Exposed |
500 |
9,500 |
10,000 |
|
0.050 |
|
Not Exposed |
900 |
89,100 |
90,000 |
|
0.010 |
|
Column Totals |
1,400 |
98,600 |
100,000 |
|
0.014 |
The attributable proportion for the entire population is the (incidence) risk in the overall population that can be attributed to the exposure. In the table above there are 1,400 total cases in the "Diseased" column, but only 500 of these had the exposure of interest. None of the other 900 cases can be attributed to the exposure, because they were not exposed. Consequently, only 500/1,400 = 0.357, or 35.7% of the diseased subjects were exposed (35.7% is the proportion of exposed cases).
However, not all of these diseased cases can be attributed to the exposure.We know from our previous calculation of the attributable fraction in the exposed group that the attributable fraction for the exposed group was 0.8, or 80%. Therefore, for the entire population, the fraction of cases that can be attributed to the exposure is 0.357 x 0.80 = 0.286, or 28.6%.
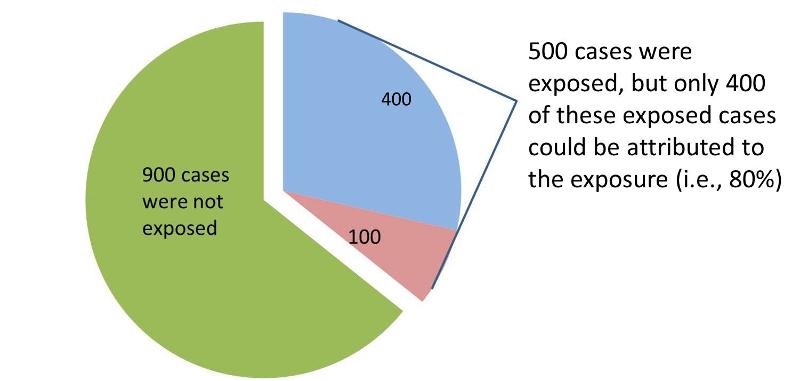
Interpretation:
28.6% of all cases in the population are attributable to the exposure.
Another way to look at this is to look at the pie chart above and consider that only 400 of the exposed cases could be attributed to the exposure, but in the population there were a total of 1,400 cases. So, 400/1400 = 28.6%, the proportion of all cases in the population that could be attributed to the exposure.
This calculation can be summarized as follows:
Population Attributable Fraction (PAF) = (proportion of cases exposed) x (attributable proportion in the exposed)
This is the proportion (fraction) of all cases in the population that can be attributed to the exposure.
Another equivalent method that can be useful is the following:
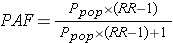
where Ppop = the proportion of exposed subjects in the entire study population, and RR = the risk or rate ratio. This formulation can be especially helpful if you have an estimate of the proportion of exposed subjects in a population from an external source, such as a population survey. For example, if we know that the relative risk for the effect of smoking on lung cancer is approximately 20, and our surveillance system data tell us that 20% of the adult population of the U.S. smokes, we can calculate the proportion of all lung cancer cases in the population that are attributable to smoking:
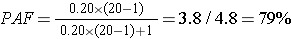
Interpretation:
79% of all cases of lung cancer in the U.S. are attributable to smoking.
All the examples above were for cohort studies or clinical trials in which we compared either cumulative incidence or incidence rates among two or more exposure groups. However, in a true case-control study we don't measure and compare incidence. There is no "follow-up" period in case-control studies.
In the module on Overview of Analytic Studies we considered a rare disease in a source population that looked like this:
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
7 |
1,000 |
1,007 |
|
Non-exposed |
6 |
5,634 |
5,640 |
This view of the population is hypothetical because it shows us the exposure status of all subjects in the population. We therefore know the total number of exposed and non-exposed people (in the "Total" column). If we know all this, we could compute the incidence in each group (the incidence in the exposed individuals would be 7/1,007 = 0.70%, and the incidence in the non-exposed individuals would be 6/5,640 = 0.11%), and we could compute the risk ratio (RR = 6.53). All of our computations involved the "Diseased" column and the "Total" column.
Another way of looking at this association is to consider that the "Diseased" column tells us the relative exposure status in people who developed the outcome (7/6 = 1.16667), and the "Total" column tells us the relative exposure status of the entire source population (1,007/5,640 = 0.1785). The ratio of these two distributions (7/6)/(1,007/5,640) = 6.53, because it is just an algebraic rearrangement of the same four numbers we used to compute the cumulative incidences and the risk ratio. Note also that the relative exposure distribution in the "Total" population is very similar the relative exposure distribution in the "Non-diseased" portion of the source population, because the disease is rare. Consequently, in order to estimate the risk ratio we could use the relative distribution of exposure in the "Non-diseased" subjects - OR, to be more efficient, we could just take a sample of non-diseased subjects in order to estimate their exposure distribution. We could for example, just sample 1% of the non-diseased people and I then determine their exposure status. The data might look something like this:
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
7 |
10 |
unknown |
|
Non-exposed |
6 |
56 |
unknown |
The relative exposure distributions (7/6) and (10/56) are really odds, i.e. the odds of exposure among cases and non-diseased controls. If we compute the ratio of these two odds we would get:
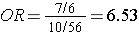
i.e., almost identical to the risk ratio we calculated when we had all the information for the source group. Note that we would get the same answer if we computed the odds ratio by dividing the odds of disease in the exposed (7/10) by the the odds of disease in the non-exposed group (6/56).
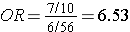
because this expression is just an algebraic rearrangement of the previous equation.
Provided that the disease is uncommon (say <10%), this sampling approach gives an odds ratio that is a reasonably good estimate of the risk ratio. Very rare outcomes (e.g., in the tables above) will give odds ratios that are extremely close to what the risk ratio would be. However, as the outcomes of interest become more common, the odds ratio gives estimates that are increasing more extreme than the risk ratio would have been. By more extreme, I mean that odds ratios that are greater than 1 will be larger than the corresponding risk ratio, and odds ratios that are less than 1 will be smaller than the corresponding risk ratio.
The figure below depict shows that when the outcome is more common (e.g., >10%), the odds ratio exaggerates the estimated strength of association.
|
|
Diseased |
Non-Diseased |
Total |
Cumulative Incidence |
|
Exposed |
60 |
108 |
168 |
60/(60+108) = 35.7% |
|
Non-Exposed |
45 |
341 |
386 |
45/(45+341) = 11.7% |
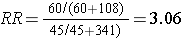
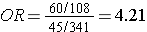
The interactive feature below allows you to simultaneously compute both the risk ratio and the odds ratio in a hypothetical cohort study. In general, the odds ratio will be close in value to the risk ratio when the outcome of interest is rare, but the odds ratio will tend to become more extreme than the risk ratio as the outcome becomes increasingly common.You can use this widget to observe how the odds and probabilities change as you make the outcome more common. For example, enter numbers in the cells that would be consistent with a rare outcome and compare the OR and the RR. Then increase the frequency of the outcome by doubling, quadrupling, etc. the number of events in the first column without changing the second column.
|
Key Concept: Remember that in a cohort study you can calculate either a risk ratio or an odds ratio, but In a case-control study: you can only calculate an odds ratio.
|
In a cohort type study, one can calculate the incidence in each group, the risk ratio, the risk difference, and the attributable fraction. In addition, one can also calculate an odds ratio in a cohort study, as we did in the two examples immediately above. In contrast, in a case-control study one can only calculate the odds ratio, i.e. an estimate of relative effect size, because one cannot calculate incidence. Consider once again the table that we used above to illustrate calculation of the odds ratio.
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
7 |
10 |
unknown |
|
Non-exposed |
6 |
56 |
unknown |
In this table the total number of exposed and non-exposed subjects is not known, because sampling was done using a case-control design. One might find many or all of the cases in a source population, particularly if it is a reportable disease. In this example, the investigators found all thirteen cases, but then they just sampled 66 non-diseased people in order to estimate the exposure distribution in the source population. When a case-control approach is used for sampling, we don't know how many exposed people it took to generate the 7 cases in the first row, and we don't know how many non-exposed persons were needed to generate the 6 cases in the second row. The information from non-diseased controls allow us to estimate the exposure distribution in the source population, .we don't know the denominators ("Totals") for either exposure group.
While it is generally not possible to calculate the absolute risk of disease (incidence) in a case control study, it is possible to estimate the attributable proportion among the exposed (AR%). It was noted earlier in the module that the attributable proportion among the exposed in cohort type studies can also be calculated from the formula:
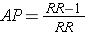
Since the OR is an estimate of RR, then by analogy the attributable proportion among the exposed can be estimated in a case-control study from the formula:
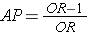
This can also be expressed as a percentage by multiplying by 100.
Finally, since it is possible to estimate the attributable proportion in the exposed in a case-control study, it is also possible to compute the population attributable proportion in an analogous way to the computation in cohort type studies, i.e.,
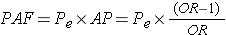
where Pe is the proportion of cases that have the exposure.




