Evaluating Effect Modification With Multiple Linear Regression

---

Considered data from a clinical trial designed to evaluate the efficacy of a new drug to increase HDL cholesterol. One hundred patients enrolled in the study and were randomized to receive either the new drug or a placebo. The investigators were at first disappointed to find very little difference in the mean HDL cholesterol levels of treated and untreated subjects.

	Sample Size	Mean HDL	Standard Deviation of HDL
New Drug	50	40.16	4.48
Placebo	50	39.21	3.91

However, when they analyzed the data separately in men and women, they found evidence of an effect in men, but not in women. We noted that when the magnitude of association differs at different levels of another variable (in this case gender), it suggests that effect modification is present.

WOMEN	Sample Size	Mean HDL	Standard Deviation of HDL
New Drug	40	38.88	3.97
Placebo	41	39.24	4.21

 

Men	Sample Size	Mean HDL	Standard Deviation of HDL
New Drug	10	45.25	1.89
Placebo	9	39.06	2.22

Multiple regression analysis can be used to assess effect modification. This is done by estimating a multiple regression equation relating the outcome of interest (Y) to independent variables representing the treatment assignment, sex and the product of the two (called the treatment by sex interaction variable). For the analysis, we let T = the treatment assignment (1=new drug and 0=placebo), M = male gender (1=yes, 0=no) and TM, i.e., T * M or T x M, the product of treatment and male gender. In this case, the multiple regression analysis revealed the following: 

Independent Variable	Regression Coefficient	T	P-value
Intercept	39.24	65.89	0.0001
T (Treatment)	-0.36	-0.43	0.6711
M (Male Gender)	-0.18	-0.13	0.8991
TM (Treatment x Male Gender)	6.55	3.37	0.0011

The multiple regression model is:

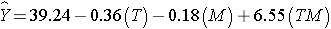
The details of the test are not shown here, but note in the table above that in this model, the regression coefficient associated with the interaction term, b₃, is statistically significant (i.e., H₀: b₃ = 0 versus H₁: b₃ ≠ 0). The fact that this is statistically significant indicates that the association between treatment and outcome differs by sex.

The model shown above can be used to estimate the mean HDL levels for men and women who are assigned to the new medication and to the placebo. In order to use the model to generate these estimates, we must recall the coding scheme (i.e., T = 1 indicates new drug, T=0 indicates placebo, M=1 indicates male sex and M=0 indicates female sex).

The expected or predicted HDL for men (M=1) assigned to the new drug (T=1) can be estimated as follows:

 

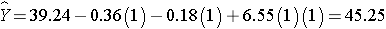
The expected HDL for men (M=1) assigned to the placebo (T=0) is:

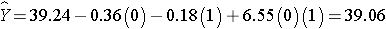
Similarly, the expected HDL for women (M=0) assigned to the new drug (T=1) is:

 

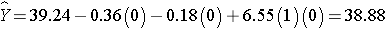
The expected HDL for women (M=0)assigned to the placebo (T=0) is:

 

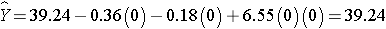
Notice that the expected HDL levels for men and women on the new drug and on placebo are identical to the means shown the table summarizing the stratified analysis. Because there is effect modification, separate simple linear regression models are estimated to assess the treatment effect in men and women:

MEN	Regression Coefficient	T	P-value
Intercept	39.08	57.09	0.0001
T (Treatment)	6.19	6.56	0.0001
WOMEN	Regression Coefficient	T	P-value
Intercept	39.24	61.36	0.0001
T (Treatment)	-0.36	-0.40	0.6927

 The regression models are:

In Men:

 

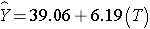
In Women:

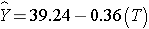
In men, the regression coefficient associated with treatment (b₁=6.19) is statistically significant (details not shown), but in women, the regression coefficient associated with treatment (b₁= -0.36) is not statistically significant (details not shown).

Multiple linear regression analysis is a widely applied technique. In this section we showed here how it can be used to assess and account for confounding and to assess effect modification. The techniques we described can be extended to adjust for several confounders simultaneously and to investigate more complex effect modification (e.g., three-way statistical interactions).

There is an important distinction between confounding and effect modification. Confounding is a distortion of an estimated association caused by an unequal distribution of another risk factor. When there is confounding, we would like to account for it (or adjust for it) in order to estimate the association without distortion. In contrast, effect modification is a biological phenomenon in which the magnitude of association is differs at different levels of another factor, e.g., a drug that has an effect on men, but not in women. In the example, present above it would be in inappropriate to pool the results in men and women. Instead, the goal should be to describe effect modification and report the different effects separately.

 

There are many other applications of multiple regression analysis. A popular application is to assess the relationships between several predictor variables simultaneously, and a single, continuous outcome. For example, it may be of interest to determine which predictors, in a relatively large set of candidate predictors, are most important or most strongly associated with an outcome. It is always important in statistical analysis, particularly in the multivariable arena, that statistical modeling is guided by biologically plausible associations.

"Dummy" Variables in Regression Models 

Independent variables in regression models can be continuous or dichotomous. Regression models can also accommodate categorical independent variables. For example, it might be of interest to assess whether there is a difference in total cholesterol by race/ethnicity. The module on Hypothesis Testing presented analysis of variance as one way of testing for differences in means of a continuous outcome among several comparison groups. Regression analysis can also be used. However, the investigator must create indicator variables to represent the different comparison groups (e.g., different racial/ethnic groups). The set of indicator variables (also called dummy variables) are considered in the multiple regression model simultaneously as a set independent variables.

For example, suppose that participants indicate which of the following best represents their race/ethnicity: White, Black or African American, American Indian or Alaskan Native, Asian, Native Hawaiian or Pacific Islander or Other Race. This categorical variable has 6 response options. To consider race/ethnicity as a predictor in a regression model, we create five indicator variables (one less than the total number of response options) to represent the 6 different groups. To create the set of indicators, or set of dummy variables, we first decide on a reference group or category. In this example, the reference group is the racial group that we will compare the other groups against. Indicator variable are created for the remaining groups are coded 1 for participants who are in that group (e.g., are of the specific race/ethnicity of interest), and all others are coded 0. In the multiple regression model, the regression coefficients associated with each of the dummy variables (representing in this example each race/ethnicity group) are interpreted as the expected difference in the mean of the outcome variable for that race/ethnicity as compared to the reference group, holding all other predictors constant. The example below uses an investigation of risk factors for low birth weight to illustrates this technique as well as the interpretation of the regression coefficients in the model.

Example of the Use of Dummy Variables

An observational study is conducted to investigate risk factors associated with infant birth weight. The study involves 832 pregnant women. Each woman provides demographic and clinical data and is followed through the outcome of pregnancy. At the time of delivery, the infant s birth weight (grams) is measures, as is their gestational age (weeks). Birth weights vary widely and range from 404 to 5400 grams. The mean birth weight is 3367.83 grams with a standard deviation of 537.21 grams. Investigators wish to determine whether there are differences in birth weight by infant gender, gestational age, mother's age and mother's race. In the study sample, 421/832 (50.6%) of the infants are male and the mean gestational age at birth is 39.49 weeks with a standard deviation of 1.81 weeks (range 22-43 weeks). The mean mother's age is 30.83 years with a standard deviation of 5.76 years (range 17-45 years). Approximately 49% of the mothers are white; 41% are Hispanic; 5% are black; and 5% identify themselves as other race. A multiple regression analysis is performed relating infant gender (coded 1=male, 0=female), gestational age in weeks, mother's age in years and 3 dummy or indicator variables reflecting mother's race. The results are summarized in the table below.

Independent Variable	Regression Coeffcient	T	P-value
Intercept	-3850.92	-11.56	0.0001
Male infant	174.79	6.06	0.0001
Gestational age (weeks)	179.89	22.35	0.0001
Mother's age (yrs.)	1.38	0.47	0.6361
Black race	-138.46	-1.93	0.0535
Hispanic race	-13.07	-0.37	0.7103
Other race	-68.67	-1.05	0.2916

Many of the predictor variables are statistically significantly associated with birth weight. Male infants are approximately 175 grams heavier than female infants, adjusting for gestational age, mother's age and mother's race/ethnicity. Gestational age is highly significant (p=0.0001), with each additional gestational week associated with an increase of 179.89 grams in birth weight, holding infant gender, mother's age and mother's race/ethnicity constant. Mother's age does not reach statistical significance (p=0.6361). Mother's race is modeled as a set of three dummy or indicator variables. In this analysis, white race is the reference group. Infants born to black mothers have lower birth weight by approximately 140 grams (as compared to infants born to white mothers), adjusting for gestational age, infant gender and mothers age. This difference is marginally significant (p=0.0535). There are no statistically significant differences in birth weight in infants born to Hispanic versus white mothers or to women who identify themselves as other race as compared to white.

return to top | previous page | next page