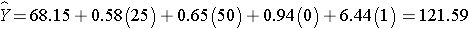The Multiple Linear Regression Equation
The multiple linear regression equation is as follows:
,
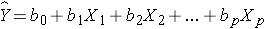where 
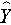is the predicted or expected value of the dependent variable, X1 through Xp are p distinct independent or predictor variables, b0 is the value of Y when all of the independent variables (X1 through Xp) are equal to zero, and b1 through bp are the estimated regression coefficients. Each regression coefficient represents the change in Y relative to a one unit change in the respective independent variable. In the multiple regression situation, b1, for example, is the change in Y relative to a one unit change in X1, holding all other independent variables constant (i.e., when the remaining independent variables are held at the same value or are fixed). Again, statistical tests can be performed to assess whether each regression coefficient is significantly different from zero.
Identifying & Controlling for Confounding With Multiple Linear Regression
As suggested on the previous page, multiple regression analysis can be used to assess whether confounding exists, and, since it allows us to estimate the association between a given independent variable and the outcome holding all other variables constant, multiple linear regression also provides a way of adjusting for (or accounting for) potentially confounding variables that have been included in the model.
Suppose we have a risk factor or an exposure variable, which we denote X1 (e.g., X1=obesity or X1=treatment), and an outcome or dependent variable which we denote Y. We can estimate a simple linear regression equation relating the risk factor (the independent variable) to the dependent variable as follows:
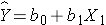
where b1 is the estimated regression coefficient that quantifies the association between the risk factor and the outcome.
If we now want to assess whether a third variable (e.g., age) is a confounder, we can denote the potential confounder X2, and then estimate a multiple linear regression equation as follows:
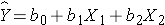
In the multiple linear regression equation, b1 is the estimated regression coefficient that quantifies the association between the risk factor X1 and the outcome, adjusted for X2 (b2 is the estimated regression coefficient that quantifies the association between the potential confounder and the outcome). As noted earlier, some investigators assess confounding by assessing how much the regression coefficient associated with the risk factor (i.e., the measure of association) changes after adjusting for the potential confounder. In this case, we compare b1 from the simple linear regression model to b1 from the multiple linear regression model. As a rule of thumb, if the regression coefficient from the simple linear regression model changes by more than 10%, then X2 is said to be a confounder.
Once a variable is identified as a confounder, we can then use multiple linear regression analysis to estimate the association between the risk factor and the outcome adjusting for that confounder. The test of significance of the regression coefficient associated with the risk factor can be used to assess whether the association between the risk factor is statistically significant after accounting for one or more confounding variables. This is also illustrated below.
Example:
The Association Between BMI and Systolic Blood Pressure
Suppose we want to assess the association between BMI and systolic blood pressure using data collected in the seventh examination of the Framingham Offspring Study. A total of n=3,539 participants attended the exam, and their mean systolic blood pressure was 127.3 with a standard deviation of 19.0. The mean BMI in the sample was 28.2 with a standard deviation of 5.3.
A simple linear regression analysis reveals the following:
|
Independent Variable |
Regression Coefficient |
T |
P-value |
|---|---|---|---|
|
Intercepte |
108.28 |
62.61 |
0.0001 |
|
BMI |
0.67 |
11.06 |
0.0001 |
The simple linear regression model is:
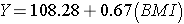
where 
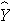is the predicted of expected systolic blood pressure. The regression coefficient associated with BMI is 0.67; each one unit increase in BMI is associated with a 0.67 unit increase in systolic blood pressure. The association between BMI and systolic blood pressure is also statistically significant (p=0.0001).
Suppose we now want to assess whether age (a continuous variable, measured in years), male gender (yes/no), and treatment for hypertension (yes/no) are potential confounders, and if so, appropriately account for these using multiple linear regression analysis. For analytic purposes, treatment for hypertension is coded as 1=yes and 0=no. Gender is coded as 1=male and 0=female. A multiple regression analysis reveals the following:
|
Independent Variable |
Regression Coefficient |
T |
P-value |
|---|---|---|---|
|
Intercept |
68.15 |
26.33 |
0.0001 |
|
BMI |
-0.58 |
10.30 |
0.0001 |
|
Age |
0.65 |
20.22 |
0.0001 |
|
Male gender |
0.94 |
1.58 |
0.1133 |
|
Treatment for hypertension |
6.44 |
9.74 |
0.0001 |
The multiple regression model is:
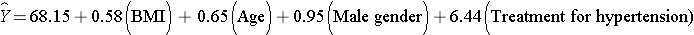
Notice that the association between BMI and systolic blood pressure is smaller (0.58 versus 0.67) after adjustment for age, gender and treatment for hypertension. BMI remains statistically significantly associated with systolic blood pressure (p=0.0001), but the magnitude of the association is lower after adjustment. The regression coefficient decreases by 13%.
[Note: Some investigators compute the percent change using the adjusted coefficient as the "beginning value," since it is theoretically unconfounded. With this approach the percent change would be = 0.09/0.58 = 15.5%. Both approaches are used, and the results are usually quite similar.]
Using the informal 10% rule (i.e., a change in the coefficient in either direction by 10% or more), we meet the criteria for confounding. Thus, part of the association between BMI and systolic blood pressure is explained by age, gender, and treatment for hypertension.
This suggests a useful way of identifying confounding. Typically, we try to establish the association between a primary risk factor and a given outcome after adjusting for one or more other risk factors. One useful strategy is to use multiple regression models to examine the association between the primary risk factor and the outcome before and after including possible confounding factors. If the inclusion of a possible confounding variable in the model causes the association between the primary risk factor and the outcome to change by 10% or more, then the additional variable is a confounder.
Relative Importance of the Independent Variables
Assessing only the p-values suggests that these three independent variables are equally statistically significant. The magnitude of the t statistics provides a means to judge relative importance of the independent variables. In this example, age is the most significant independent variable, followed by BMI, treatment for hypertension and then male gender. In fact, male gender does not reach statistical significance (p=0.1133) in the multiple regression model. Some investigators argue that regardless of whether an important variable such as gender reaches statistical significance it should be retained in the model in order to control for possible confounding. Other investigators only retain variables that are statistically significant.
This is yet another example of the complexity involved in multivariable modeling. The multiple regression model produces an estimate of the association between BMI and systolic blood pressure that accounts for differences in systolic blood pressure due to age, gender and treatment for hypertension.
A one unit increase in BMI is associated with a 0.58 unit increase in systolic blood pressure holding age, gender and treatment for hypertension constant. Each additional year of age is associated with a 0.65 unit increase in systolic blood pressure, holding BMI, gender and treatment for hypertension constant.
Men have higher systolic blood pressures, by approximately 0.94 units, holding BMI, age and treatment for hypertension constant and persons on treatment for hypertension have higher systolic blood pressures, by approximately 6.44 units, holding BMI, age and gender constant. The multiple regression equation can be used to estimate systolic blood pressures as a function of a participant's BMI, age, gender and treatment for hypertension status. For example, we can estimate the blood pressure of a 50 year old male, with a BMI of 25 who is not on treatment for hypertension as follows:
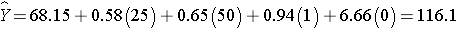
We can estimate the blood pressure of a 50 year old female, with a BMI of 25 who is on treatment for hypertension as follows:
