What is Confounding?
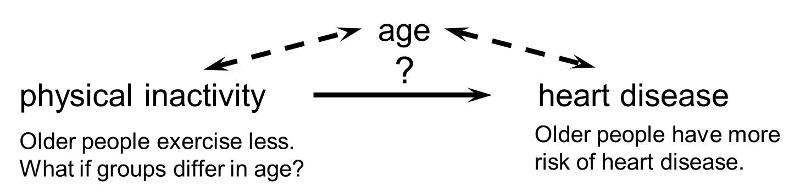
Confounding is a distortion (inaccuracy) in the estimated measure of association that occurs when the primary exposure of interest is mixed up with some other factor that is associated with the outcome. In the diagram below, the primary goal is to ascertain the strength of association between physical inactivity and heart disease. Age is a confounding factor because it is associated with the exposure (meaning that older people are more likely to be inactive), and it is also associated with the outcome (because older people are at greater risk of developing heart disease).
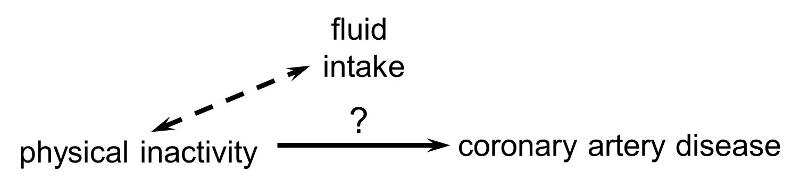
In order for confounding to occur, the extraneous factor must be associated with both the primary exposure of interest and the disease outcome of interest. For example, subjects who are physically active may drink more fluids (e.g., water and sports drinks) than inactive people, but drinking more fluid has no effect on the risk of heart disease, so fluid intake is not a confounding factor here.
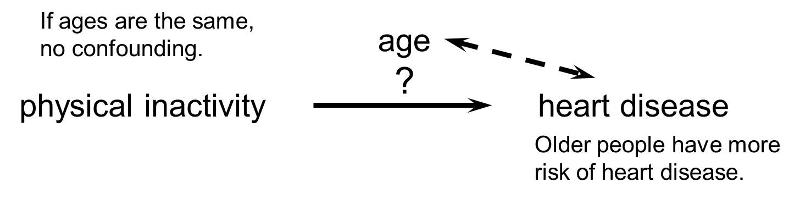
Or, if the age distribution is similar in the exposure groups being compared, then age will not cause confounding.
Refining Our Understanding of Confounding
Rothman and others use a study by Stark and Mantel
and others use a study by Stark and Mantel to illustrate the key features of confounding. These authors investigated the association between birth order and the risk of Down syndrome
to illustrate the key features of confounding. These authors investigated the association between birth order and the risk of Down syndrome . The first graph to the right shows a clear trend toward increasing prevalence of Down syndrome with increasing birth order, or an association between increasing birth order and risk of Down syndrome.
. The first graph to the right shows a clear trend toward increasing prevalence of Down syndrome with increasing birth order, or an association between increasing birth order and risk of Down syndrome.
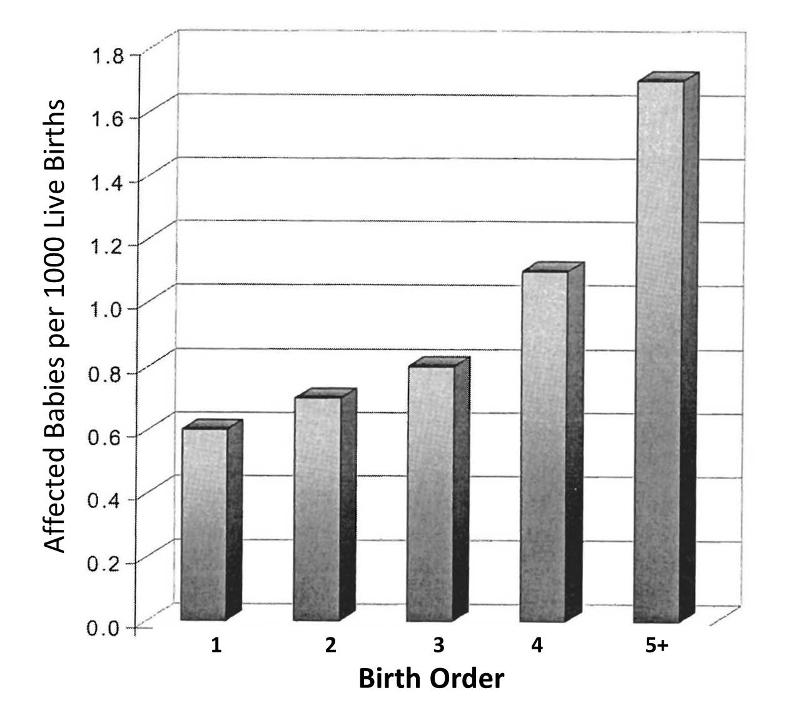
A 5th born child appears to have roughly a 4-fold increase in risk of being born with Down syndrome. Results like this also invite us to think about the mechanisms by which this occurred. Why might birth order cause a greater risk of Down syndrome? Keep in mind that this analysis does not consider any other "risk factors" besides birth order.
However, consider also that the order in which a women's children are born is also linked to her age at the time of her child's birth. When Stark and Mantel examined the relationship between maternal age at birth and risk of the child having Down syndrome, they observed the relationship depicted in the bar graph below. This shows an even more striking relationship between maternal age at birth and the child's risk of being born with Down syndrome.
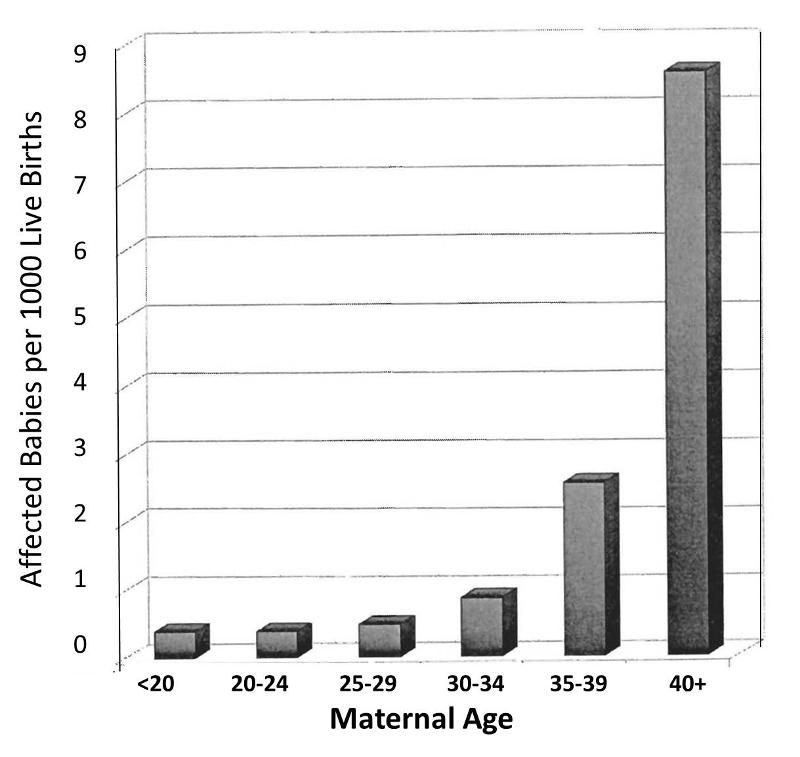
Obviously, women giving birth to their fifth child are on average, older than women giving birth to their first child. In other words, birth order of children is mixed up with maternal age when a child is born. The correlation between maternal age and prevalence of Down syndrome is much stronger than the correlation with birth order, and a woman having her 5th child is clearly older than when she gave birth to her previous children. In view of this, the relationship between birth order and prevalence of Down syndrome is confounded by age. In other words, the association between birth order and Down syndrome is exaggerated by the confounding effect of maternal age.
But is the converse also true? Is the effect of maternal age confounded by birth order? It is possible, but only if birth order really has some independent effect on the likelihood of Down syndrome, i.e. an effect independent of the fact that birth order is linked to maternal age. Rothman points out that a good way to sort this out is to look at both effects simultaneously, as in the graph below.
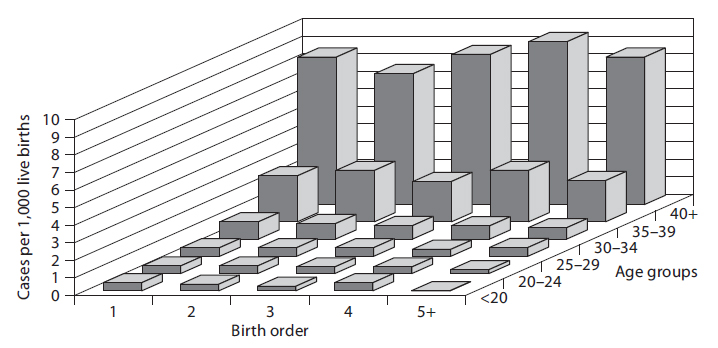
In a sense this graph shows the relationships by stratifying the prevalence of Down syndrome by both birth order and maternal age. If one focuses on how prevalence changes within any particular maternal age group looking from side to side, it is clear that increasing birth order does not correlate with the prevalence of Down syndrome. In other words, if one "controls for maternal age," there is no evidence that birth order has any impact. On the other hand, if one now examines changes in prevalence within each of the birth order groups by looking from front to back within a given birth order, there is clearly a marked increase in prevalence as maternal age increases within all five levels of birth order. In other words, even after taking birth order into account (i.e., controlling for birth order) the strong association with maternal age persists.
Based on this analysis one can conclude that the association between birth order and Down syndrome was confounded by age. The different birth order groups had different age distributions, and maternal age is clearly associated with prevalence of Down syndrome. As a result, the apparent association between birth order and and Down syndrome that was seen in the first figure was completely due to the confounding effect of age. On the other hand, the association between maternal age and Down syndrome was NOT confounded by birth order, because birth order has no impact on the prevalence of Down syndrome, and the association between age and Down was not distorted by differences in birth order.
Unraveling the Complexity of Health Problems
Most health problems have many determinants ("risk factors"), so it is not surprising that there is a lot of potential for confounding. While this can represent a barrier to testing a particular hypothesis, it is also an opportunity to dissect the many determinants and to define their relative importance.
|
In "Epidemiology - An Introduction" Ken Rothman says the following about this complexity: "The research process of learning about and controlling for confounding can be thought of as a walk through a maze toward a central goal. The path through the maze eventually permits the scientist to penetrate into levels that successively get closer to the goal: in [the example of maternal age and Down syndrome] the apparent relations between Down syndrome and birth order can be explained entirely by the effect of mother's age, but that effect in turn will ultimately be explained by other factors that have not yet been identified. As the layers of confounding are left behind, we gradually approach a deeper causal understanding of the underlying biology. Unlike a maze, however, this journey toward biologic understanding does not have a clear endpoint, in the sense that there is always room to understand the biology in a deeper way." |