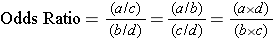The Case-Control Design

Ken Rothman, who is a world-renowned epidemiologist on our faculty, describes the case-control strategy as follows:

"Case-control studies are best understood by considering as the starting point a source population, which represents a hypothetical study population in which a cohort study might have been conducted. The source population is the population that gives rise to the cases included in the study. If a cohort study were undertaken, we would define the exposed and unexposed cohorts (or several cohorts) and from these populations obtain denominators for the incidence rates or risks that would be calculated for each cohort. We would then identify the number of cases occurring in each cohort and calculate the risk or incidence rate for each. In a case-control study the same cases are identified and classified as to whether they belong to the exposed or unexposed cohort. Instead of obtaining the denominators for the rates or risks, however, a control group is sampled from the entire source population that gives rise to the cases. Individuals in the control group are then classified into exposed and unexposed categories. The purpose of the control group is to determine the relative size of the exposed and unexposed components of the source population."

Kenneth Rothman - Epidemiology - An Introduction. Oxford University Press, 2002. p. 73

With this description in mind, let's re-examine the data from the island population with 13 cases of a rare neurological problem.

	Diseased	Non-diseased	Total
High pesticide levels	7	1,000	1,007
Low pesticide levels	6	5,634	5,640

We saw that the risk ratio can be computed by comparing the odds of exposure in the cases to the odds of exposure in the overall source population. The problem is that we do not have the resources to assess exposure in the entire population. However, note that, because this is an uncommon outcome, the exposure distribution in the "Non-diseased" column is very close to the exposure distribution in the "Total" source population. We saw previously that the odds of exposure in the total source population were 1007/5640 = 0.1785. The odds of exposure in the "Non-diseased" subjects are 1000/5634 = 0.1775. So, this provides a very reasonable estimate of the odds of exposure in the overall source population, or as Rothman says, the relative size of the exposed and unexposed componests of the source population. And, if all we need is an estimate of the relative size of the exposed and unexposed components of the source population, we can just take a sample of the non-diseased people and measure their pesticide levels to determine whether they were exposed or not.

We have $4,000 to spend on this, so let's measure pesticide levels in all 13 cases and a sample of 52 non-diseased "controls", i.e., four times as many controls as cases. Sampling non-diseased people to measure their pesticide levels will enable us to estimate the ratio of exposed to non-exposed people in the overall source population.

	Diseased	Non-diseased	Total
High pesticide levels	7	8	unknown
Low pesticide levels	6	44	unknown
Totals	13	52

From these data we can estimate the risk ratio from the odds ratio, i.e.,

OR = (Odds of exposure in cases) / (Odds of exposure in non-diseased controls)

OR = (7/6) / (8/44) = 6.42

Notice that with this method we cannot compute the actual incidence of disease in the two exposure groups, because this sampling method does not give us the denominators for the total number of exposed and unexposed people. However, the odds ratio does provide a reasonable estimate of the risk ratio, particularly when the outcome is uncommon. For more common outcomes, the odds ratio overestimates (i.e., is more extreme than) the risk ratio.

Also note that since we cannot compute the incidence with a case-control design, we are also unable to compute the risk difference.

Nevertheless, the case-control design can provide valuable information when dealing with rare outcomes or when exposure data is difficult to obtain. The cost of this case-control study was $50 x 65 subjects = $3,250, so we were well under budget.

A Modern Interpretation of the Odds Ratio

The odds ratio is the measure of association that can be estimated from case-control studies, and it is based on a comparison of the odds of exposure in cases and controls. However, modern epidemiologists view the case-control design as a more efficient version of a cohort study, and they interpret the results in a similar fashion.

	Cases (Diseased)	Controls (Non-diseased)
High pesticide Levels	7	8
Low pesticide levels	6	44
Totals	13	52

The odds ratio was computed as the odds of high pesticide exposure in cases compared to the odds of high pesticide exposure in controls.

OR= (7/6) / 8/44) = 6.42

However, algebraic rearrangement provides another way of computing and interpreting this, i.e., as the odds of disease among those with high pesticide levels compared to the odds of disease in those with low pesticide levels:

OR= (7/8) / (6/44) = 6.42

 Therefore, we can interpret these finding in either of two ways:

1. The cases had 6.42 times the odds of exposure compared to controls. Or
2. Exposed subjects had 6.42 times the odds of disease compared to non-exposed subjects.

The second method is preferred, so we would interpret the finding of the pesticide study as follows:

 Residents of the island with high blood levels of pesticide had 6.42 times the odds of developing the neurological disease compared to residents with low levels of the pesticide during the period of this study.

Calculating the Odds Ratio

As with cohort studies, there are two ways of orienting the contingency table summarizing the results of a case-control study as shown in the two tables below. First, with cases on row 1 and controls on row 2.

	Exposed	Unexposed
Cases	a	b
Controls	c	d

Or, by rotating the table and putting the cases and controls in the columns.

	Cases	Controls
Exposed	a	b
Unexposed	c	d

All three of these formulas for calculating the odds ratio give the same result. It is best to pick one of them and use it consistently.

return to top | previous page | next page