Another Way of Thinking About Cohort Studies
If we had had the money to analyze blood samples from all residents and examined them for evidence of the neurological problem when their blood was drawn, the results might have looked like this:
|
|
Diseased |
Non-diseased |
Total |
|
High pesticide levels |
7 |
1,000 |
1,007 |
|
Low pesticide levels |
6 |
5,634 |
5,640 |
Therefore, the incidence in the exposed individuals would be 7/1,007 = 0.70%, and the incidence in the non-exposed individuals would be 6/5,640 = 0.11%. Consequently, the risk ratio would be (7/1007) / (6/5640) = 6.53, suggesting that those exposed to the pesticide had 6.5 times the risk of getting the disease compared to those with low levels. This is a strong association.
To compute this risk ratio we used the number of diseased people in each group and the total number of people in each exposure group to compute the cumulative incidence in each group and then divided to get the risk ratio.
An alternative way of thinking about the same information is to think about the likelihood of exposure among the diseased cases (i.e., the odds of exposure in cases) compared to the likelihood of exposure in the overall source population. The odds of exposure in the case group were 7/6, while the odds of exposure in the overall source population were 1,007/5,640. Exposure was much more likely in the cases. In fact, the odds ratio was (7/6) / (1,007/5,640) = 1.1667/0.1785 = 6.53. This is just another method of computing the risk ratio, because this is just an algebraic rearrangement of the risk ratio.
This is demonstrated in the sequence of equations shown below.

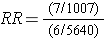
But dividing by a fraction is equivalent to multiply by its reciprocal, so

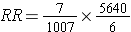
Which rearranges to:

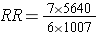
Which is the same as:

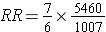
And multiplying by a fraction is equivalent to dividing by its reciprocal, so:

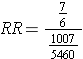
The point is that we can compute a risk ratio by computing the ratio
RR = CIe/CIu
... or by computing the exposure distribution in the diseased cases divided by the exposure distribution in the source population:
RR = (Odds of exposure in cases) / (Odds of exposure in overall source population)
In the next section you will see how case-control studies take advantage of this to maximize efficiency.