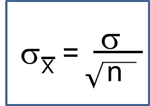Summary
This module presents hypothesis testing techniques for situations with small sample sizes and outcomes that are ordinal, ranked or continuous and cannot be assumed to be normally distributed. Nonparametric tests are based on ranks which are assigned to the ordered data. The tests involve the same five steps as parametric tests, specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. The tests are summarized below.
Mann Whitney U Test
Use: To compare a continuous outcome in two independent samples.
Null Hypothesis: H0: Two populations are equal
Test Statistic: The test statistic is U, the smaller of

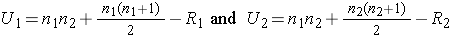
where R1 and R2 are the sums of the ranks in groups 1 and 2, respectively.
Decision Rule: Reject H0 if U < critical value from table
Sign Test
Use: To compare a continuous outcome in two matched or paired samples.
Null Hypothesis: H0: Median difference is zero
Test Statistic: The test statistic is the smaller of the number of positive or negative signs.
Decision Rule: Reject H0 if the smaller of the number of positive or negative signs < critical value from table.
Wilcoxon Signed Rank Test
Use: To compare a continuous outcome in two matched or paired samples.
Null Hypothesis: H0: Median difference is zero
Test Statistic: The test statistic is W, defined as the smaller of W+ and W- which are the sums of the positive and negative ranks of the difference scores, respectively.
Decision Rule: Reject H0 if W < critical value from table.
Kruskal Wallis Test
Use: To compare a continuous outcome in more than two independent samples.
Null Hypothesis: H0: k population medians are equal
Test Statistic: The test statistic is H,

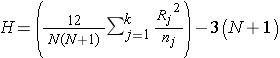
where k=the number of comparison groups, N= the total sample size, nj is the sample size in the jth group and Rj is the sum of the ranks in the jth group.
Decision Rule: Reject H0 if H > critical value
|
Key Concept: It is important to note that nonparametric tests are subject to the same errors as parametric tests. A Type I error occurs when a test incorrectly rejects the null hypothesis. A Type II error occurs when a test fails to reject H0 when it is false. Power is the probability of a test to correctly reject H0. Nonparametric tests can be subject to low power mainly due to small sample size. Therefore, it is important to consider the possibility of a Type II error when a nonparametric test fails to reject H0. There may be a true effect or difference, yet the nonparametric test is underpowered to detect it. For more details, interested readers should see Conover and Siegel and Castellan.3,4
|