
Nonparametric Tests
Author:
Lisa Sullivan, PhD
Professor of Biostatistics
Boston University School of Public Health

The three modules on hypothesis testing presented a number of tests of hypothesis for continuous, dichotomous and discrete outcomes. Tests for continuous outcomes focused on comparing means, while tests for dichotomous and discrete outcomes focused on comparing proportions. All of the tests presented in the modules on hypothesis testing are called parametric tests and are based on certain assumptions. For example, when running tests of hypothesis for means of continuous outcomes, all parametric tests assume that the outcome is approximately normally distributed in the population. This does not mean that the data in the observed sample follows a normal distribution, but rather that the outcome follows a normal distribution in the full population which is not observed. For many outcomes, investigators are comfortable with the normality assumption (i.e., most of the observations are in the center of the distribution while fewer are at either extreme). It also turns out that many statistical tests are robust, which means that they maintain their statistical properties even when assumptions are not entirely met. Tests are robust in the presence of violations of the normality assumption when the sample size is large based on the Central Limit Theorem (see page 11 in the module on Probability). When the sample size is small and the distribution of the outcome is not known and cannot be assumed to be approximately normally distributed, then alternative tests called nonparametric tests are appropriate.
After completing this module, the student will be able to:

Nonparametric tests are sometimes called distribution-free tests because they are based on fewer assumptions (e.g., they do not assume that the outcome is approximately normally distributed). Parametric tests involve specific probability distributions (e.g., the normal distribution) and the tests involve estimation of the key parameters of that distribution (e.g., the mean or difference in means) from the sample data. The cost of fewer assumptions is that nonparametric tests are generally less powerful than their parametric counterparts (i.e., when the alternative is true, they may be less likely to reject H0).
It can sometimes be difficult to assess whether a continuous outcome follows a normal distribution and, thus, whether a parametric or nonparametric test is appropriate. There are several statistical tests that can be used to assess whether data are likely from a normal distribution. The most popular are the Kolmogorov-Smirnov test, the Anderson-Darling test, and the Shapiro-Wilk test1. Each test is essentially a goodness of fit test and compares observed data to quantiles of the normal (or other specified) distribution. The null hypothesis for each test is H0: Data follow a normal distribution versus H1: Data do not follow a normal distribution. If the test is statistically significant (e.g., p<0.05), then data do not follow a normal distribution, and a nonparametric test is warranted. It should be noted that these tests for normality can be subject to low power. Specifically, the tests may fail to reject H0: Data follow a normal distribution when in fact the data do not follow a normal distribution. Low power is a major issue when the sample size is small - which unfortunately is often when we wish to employ these tests. The most practical approach to assessing normality involves investigating the distributional form of the outcome in the sample using a histogram and to augment that with data from other studies, if available, that may indicate the likely distribution of the outcome in the population.
There are some situations when it is clear that the outcome does not follow a normal distribution. These include situations:
Consider a clinical trial where study participants are asked to rate their symptom severity following 6 weeks on the assigned treatment. Symptom severity might be measured on a 5 point ordinal scale with response options: Symptoms got much worse, slightly worse, no change, slightly improved, or much improved. Suppose there are a total of n=20 participants in the trial, randomized to an experimental treatment or placebo, and the outcome data are distributed as shown in the figure below.
Distribution of Symptom Severity in Total Sample
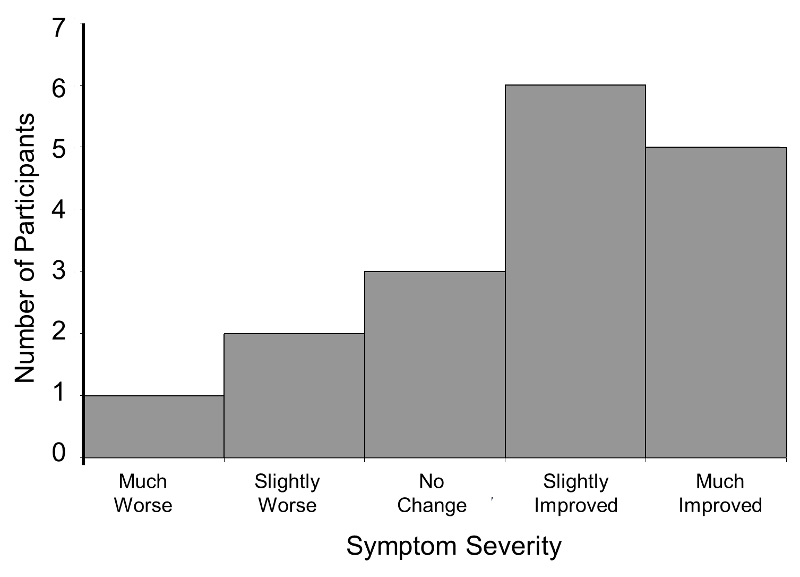
The distribution of the outcome (symptom severity) does not appear to be normal as more participants report improvement in symptoms as opposed to worsening of symptoms.
In some studies, the outcome is a rank. For example, in obstetrical studies an APGAR score is often used to assess the health of a newborn. The score, which ranges from 1-10, is the sum of five component scores based on the infant's condition at birth. APGAR scores generally do not follow a normal distribution, since most newborns have scores of 7 or higher (normal range).
In some studies, the outcome is continuous but subject to outliers or extreme values. For example, days in the hospital following a particular surgical procedure is an outcome that is often subject to outliers. Suppose in an observational study investigators wish to assess whether there is a difference in the days patients spend in the hospital following liver transplant in for-profit versus nonprofit hospitals. Suppose we measure days in the hospital following transplant in n=100 participants, 50 from for-profit and 50 from non-profit hospitals. The number of days in the hospital are summarized by the box-whisker plot below.
Distribution of Days in the Hospital Following Transplant
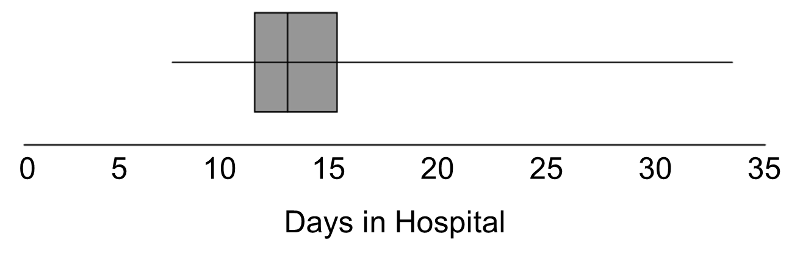
Note that 75% of the participants stay at most 16 days in the hospital following transplant, while at least 1 stays 35 days which would be considered an outlier. Recall from page 8 in the module on Summarizing Data that we used Q1-1.5(Q3-Q1) as a lower limit and Q3+1.5(Q3-Q1) as an upper limit to detect outliers. In the box-whisker plot above, 10.2, Q1=12 and Q3=16, thus outliers are values below 12-1.5(16-12) = 6 or above 16+1.5(16-12) = 22.
In some studies, the outcome is a continuous variable that is measured with some imprecision (e.g., with clear limits of detection). For example, some instruments or assays cannot measure presence of specific quantities above or below certain limits. HIV viral load is a measure of the amount of virus in the body and is measured as the amount of virus per a certain volume of blood. It can range from "not detected" or "below the limit of detection" to hundreds of millions of copies. Thus, in a sample some participants may have measures like 1,254,000 or 874,050 copies and others are measured as "not detected." If a substantial number of participants have undetectable levels, the distribution of viral load is not normally distributed.
|
Hypothesis Testing with Nonparametric Tests In nonparametric tests, the hypotheses are not about population parameters (e.g., μ=50 or μ1=μ2). Instead, the null hypothesis is more general. For example, when comparing two independent groups in terms of a continuous outcome, the null hypothesis in a parametric test is H0: μ1 =μ2. In a nonparametric test the null hypothesis is that the two populations are equal, often this is interpreted as the two populations are equal in terms of their central tendency.
|
Nonparametric tests have some distinct advantages. With outcomes such as those described above, nonparametric tests may be the only way to analyze these data. Outcomes that are ordinal, ranked, subject to outliers or measured imprecisely are difficult to analyze with parametric methods without making major assumptions about their distributions as well as decisions about coding some values (e.g., "not detected"). As described here, nonparametric tests can also be relatively simple to conduct.
This module will describe some popular nonparametric tests for continuous outcomes. Interested readers should see Conover3 for a more comprehensive coverage of nonparametric tests.
|
Key Concept:
Parametric tests are generally more powerful and can test a wider range of alternative hypotheses. It is worth repeating that if data are approximately normally distributed then parametric tests (as in the modules on hypothesis testing) are more appropriate. However, there are situations in which assumptions for a parametric test are violated and a nonparametric test is more appropriate. |
The techniques described here apply to outcomes that are ordinal, ranked, or continuous outcome variables that are not normally distributed. Recall that continuous outcomes are quantitative measures based on a specific measurement scale (e.g., weight in pounds, height in inches). Some investigators make the distinction between continuous, interval and ordinal scaled data. Interval data are like continuous data in that they are measured on a constant scale (i.e., there exists the same difference between adjacent scale scores across the entire spectrum of scores). Differences between interval scores are interpretable, but ratios are not. Temperature in Celsius or Fahrenheit is an example of an interval scale outcome. The difference between 30º and 40º is the same as the difference between 70º and 80º, yet 80º is not twice as warm as 40º. Ordinal outcomes can be less specific as the ordered categories need not be equally spaced. Symptom severity is an example of an ordinal outcome and it is not clear whether the difference between much worse and slightly worse is the same as the difference between no change and slightly improved. Some studies use visual scales to assess participants' self-reported signs and symptoms. Pain is often measured in this way, from 0 to 10 with 0 representing no pain and 10 representing agonizing pain. Participants are sometimes shown a visual scale such as that shown in the upper portion of the figure below and asked to choose the number that best represents their pain state. Sometimes pain scales use visual anchors as shown in the lower portion of the figure below.
Visual Pain Scale
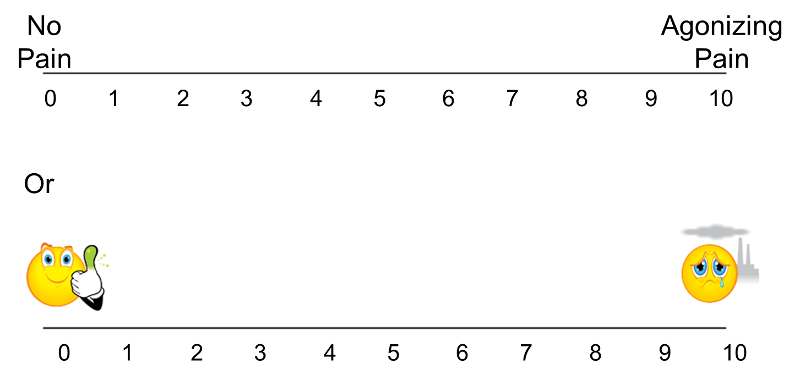
In the upper portion of the figure, certainly 10 is worse than 9, which is worse than 8; however, the difference between adjacent scores may not necessarily be the same. It is important to understand how outcomes are measured to make appropriate inferences based on statistical analysis and, in particular, not to overstate precision.
The nonparametric procedures that we describe here follow the same general procedure. The outcome variable (ordinal, interval or continuous) is ranked from lowest to highest and the analysis focuses on the ranks as opposed to the measured or raw values. For example, suppose we measure self-reported pain using a visual analog scale with anchors at 0 (no pain) and 10 (agonizing pain) and record the following in a sample of n=6 participants:
7 5 9 3 0 2
The ranks, which are used to perform a nonparametric test, are assigned as follows: First, the data are ordered from smallest to largest. The lowest value is then assigned a rank of 1, the next lowest a rank of 2 and so on. The largest value is assigned a rank of n (in this example, n=6). The observed data and corresponding ranks are shown below:
|
Ordered Observed Data: |
0 |
2 |
3 |
5 |
7 |
9 |
|
Ranks: |
1 |
2 |
3 |
4 |
5 |
6 |
A complicating issue that arises when assigning ranks occurs when there are ties in the sample (i.e., the same values are measured in two or more participants). For example, suppose that the following data are observed in our sample of n=6:
Observed Data: 7 7 9 3 0 2
The 4th and 5th ordered values are both equal to 7. When assigning ranks, the recommended procedure is to assign the mean rank of 4.5 to each (i.e. the mean of 4 and 5), as follows:
|
Ordered Observed Data: |
0.5 |
2.5 |
3.5 |
7 |
7 |
9 |
|
Ranks: |
1.5 |
2.5 |
3.5 |
4.5 |
4.5 |
6 |
Suppose that there are three values of 7. In this case, we assign a rank of 5 (the mean of 4, 5 and 6) to the 4th, 5th and 6th values, as follows:
|
Ordered Observed Data: |
0 |
2 |
3 |
7 |
7 |
7 |
|
Ranks: |
1 |
2 |
3 |
5 |
5 |
5 |
Using this approach of assigning the mean rank when there are ties ensures that the sum of the ranks is the same in each sample (for example, 1+2+3+4+5+6=21, 1+2+3+4.5+4.5+6=21 and 1+2+3+5+5+5=21). Using this approach, the sum of the ranks will always equal n(n+1)/2. When conducting nonparametric tests, it is useful to check the sum of the ranks before proceeding with the analysis.
To conduct nonparametric tests, we again follow the five-step approach outlined in the modules on hypothesis testing.
The modules on hypothesis testing presented techniques for testing the equality of means in two independent samples. An underlying assumption for appropriate use of the tests described was that the continuous outcome was approximately normally distributed or that the samples were sufficiently large (usually n1> 30 and n2> 30) to justify their use based on the Central Limit Theorem. When comparing two independent samples when the outcome is not normally distributed and the samples are small, a nonparametric test is appropriate.
A popular nonparametric test to compare outcomes between two independent groups is the Mann Whitney U test. The Mann Whitney U test, sometimes called the Mann Whitney Wilcoxon Test or the Wilcoxon Rank Sum Test, is used to test whether two samples are likely to derive from the same population (i.e., that the two populations have the same shape). Some investigators interpret this test as comparing the medians between the two populations. Recall that the parametric test compares the means (H0: μ1=μ2) between independent groups.
In contrast, the null and two-sided research hypotheses for the nonparametric test are stated as follows:
H0: The two populations are equal versus
H1: The two populations are not equal.
This test is often performed as a two-sided test and, thus, the research hypothesis indicates that the populations are not equal as opposed to specifying directionality. A one-sided research hypothesis is used if interest lies in detecting a positive or negative shift in one population as compared to the other. The procedure for the test involves pooling the observations from the two samples into one combined sample, keeping track of which sample each observation comes from, and then ranking lowest to highest from 1 to n1+n2, respectively.
Example:
Consider a Phase II clinical trial designed to investigate the effectiveness of a new drug to reduce symptoms of asthma in children. A total of n=10 participants are randomized to receive either the new drug or a placebo. Participants are asked to record the number of episodes of shortness of breath over a 1 week period following receipt of the assigned treatment. The data are shown below.
|
Placebo |
7 |
5 |
6 |
4 |
12 |
|
New Drug |
3 |
6 |
4 |
2 |
1 |
Is there a difference in the number of episodes of shortness of breath over a 1 week period in participants receiving the new drug as compared to those receiving the placebo? By inspection, it appears that participants receiving the placebo have more episodes of shortness of breath, but is this statistically significant?
In this example, the outcome is a count and in this sample the data do not follow a normal distribution.
Frequency Histogram of Number of Episodes of Shortness of Breath
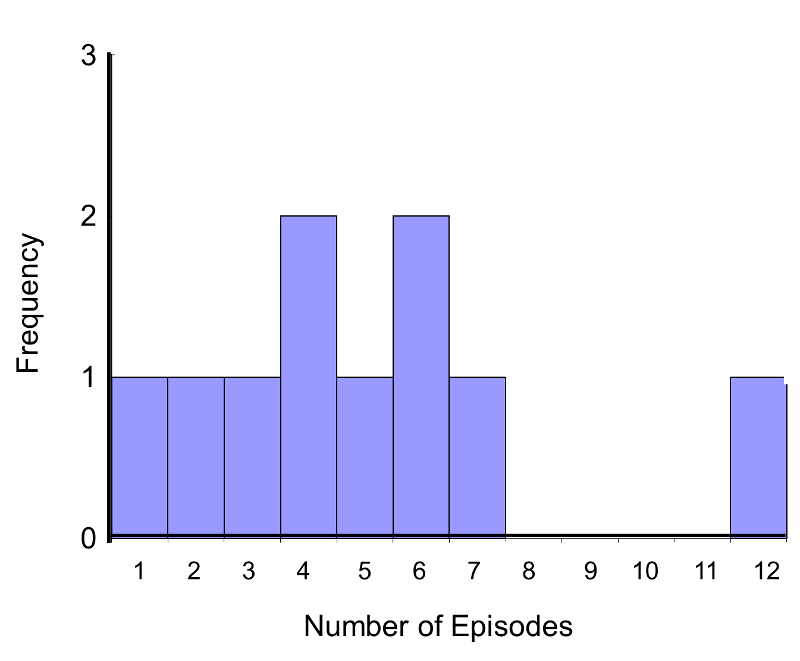
In addition, the sample size is small (n1=n2=5), so a nonparametric test is appropriate. The hypothesis is given below, and we run the test at the 5% level of significance (i.e., α=0.05).
H0: The two populations are equal versus
H1: The two populations are not equal.
Note that if the null hypothesis is true (i.e., the two populations are equal), we expect to see similar numbers of episodes of shortness of breath in each of the two treatment groups, and we would expect to see some participants reporting few episodes and some reporting more episodes in each group. This does not appear to be the case with the observed data. A test of hypothesis is needed to determine whether the observed data is evidence of a statistically significant difference in populations.
The first step is to assign ranks and to do so we order the data from smallest to largest. This is done on the combined or total sample (i.e., pooling the data from the two treatment groups (n=10)), and assigning ranks from 1 to 10, as follows. We also need to keep track of the group assignments in the total sample.
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||
|---|---|---|---|---|---|
|
Placebo |
New Drug |
Placebo |
New Drug |
Placebo |
New Drug |
|
7 |
3 |
|
1 |
|
1 |
|
5 |
6 |
|
2 |
|
2 |
|
6 |
4 |
|
3 |
|
3 |
|
4 |
2 |
4 |
4 |
4.5 |
4.5 |
|
12 |
1 |
5 |
|
6 |
|
|
|
|
6 |
6 |
7.5 |
7.5 |
|
|
|
7 |
|
9 |
|
|
|
|
12 |
|
10 |
|
Note that the lower ranks (e.g., 1, 2 and 3) are assigned to responses in the new drug group while the higher ranks (e.g., 9, 10) are assigned to responses in the placebo group. Again, the goal of the test is to determine whether the observed data support a difference in the populations of responses. Recall that in parametric tests (discussed in the modules on hypothesis testing), when comparing means between two groups, we analyzed the difference in the sample means relative to their variability and summarized the sample information in a test statistic. A similar approach is employed here. Specifically, we produce a test statistic based on the ranks.
First, we sum the ranks in each group. In the placebo group, the sum of the ranks is 37; in the new drug group, the sum of the ranks is 18. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 10(11)/2=55 which is equal to 37+18 = 55.
For the test, we call the placebo group 1 and the new drug group 2 (assignment of groups 1 and 2 is arbitrary). We let R1 denote the sum of the ranks in group 1 (i.e., R1=37), and R2 denote the sum of the ranks in group 2 (i.e., R2=18). If the null hypothesis is true (i.e., if the two populations are equal), we expect R1 and R2 to be similar. In this example, the lower values (lower ranks) are clustered in the new drug group (group 2), while the higher values (higher ranks) are clustered in the placebo group (group 1). This is suggestive, but is the observed difference in the sums of the ranks simply due to chance? To answer this we will compute a test statistic to summarize the sample information and look up the corresponding value in a probability distribution.
The test statistic for the Mann Whitney U Test is denoted U and is the smaller of U1 and U2, defined below.
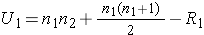
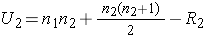
where R1 = sum of the ranks for group 1 and R2 = sum of the ranks for group 2.
For this example,
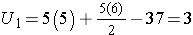
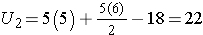
In our example, U=3. Is this evidence in support of the null or research hypothesis? Before we address this question, we consider the range of the test statistic U in two different situations.
Situation #1
Consider the situation where there is complete separation of the groups, supporting the research hypothesis that the two populations are not equal. If all of the higher numbers of episodes of shortness of breath (and thus all of the higher ranks) are in the placebo group, and all of the lower numbers of episodes (and ranks) are in the new drug group and that there are no ties, then:
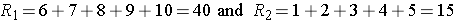
and
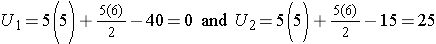
Therefore, when there is clearly a difference in the populations, U=0.
Situation #2
Consider a second situation where low and high scores are approximately evenly distributed in the two groups, supporting the null hypothesis that the groups are equal. If ranks of 2, 4, 6, 8 and 10 are assigned to the numbers of episodes of shortness of breath reported in the placebo group and ranks of 1, 3, 5, 7 and 9 are assigned to the numbers of episodes of shortness of breath reported in the new drug group, then:
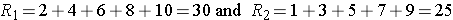 R1= 2+4+6+8+10 = 30 and R2= 1+3+5+7+9 = 25,
R1= 2+4+6+8+10 = 30 and R2= 1+3+5+7+9 = 25,
and
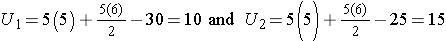
When there is clearly no difference between populations, then U=10.
Thus, smaller values of U support the research hypothesis, and larger values of U support the null hypothesis.
|
Key Concept: For any Mann-Whitney U test, the theoretical range of U is from 0 (complete separation between groups, H0 most likely false and H1 most likely true) to n1*n2 (little evidence in support of H1).
In every test, U1+U2 is always equal to n1*n2. In the example above, U can range from 0 to 25 and smaller values of U support the research hypothesis (i.e., we reject H0 if U is small). The procedure for determining exactly when to reject H0 is described below. |
In every test, we must determine whether the observed U supports the null or research hypothesis. This is done following the same approach used in parametric testing. Specifically, we determine a critical value of U such that if the observed value of U is less than or equal to the critical value, we reject H0 in favor of H1 and if the observed value of U exceeds the critical value we do not reject H0.
The critical value of U can be found in the table below. To determine the appropriate critical value we need sample sizes (for Example: n1=n2=5) and our two-sided level of significance (α=0.05). For Example 1 the critical value is 2, and the decision rule is to reject H0 if U < 2. We do not reject H0 because 3 > 2. We do not have statistically significant evidence at α =0.05, to show that the two populations of numbers of episodes of shortness of breath are not equal. However, in this example, the failure to reach statistical significance may be due to low power. The sample data suggest a difference, but the sample sizes are too small to conclude that there is a statistically significant difference.
Example:
A new approach to prenatal care is proposed for pregnant women living in a rural community. The new program involves in-home visits during the course of pregnancy in addition to the usual or regularly scheduled visits. A pilot randomized trial with 15 pregnant women is designed to evaluate whether women who participate in the program deliver healthier babies than women receiving usual care. The outcome is the APGAR score measured 5 minutes after birth. Recall that APGAR scores range from 0 to 10 with scores of 7 or higher considered normal (healthy), 4-6 low and 0-3 critically low. The data are shown below.
|
Usual Care |
8 |
7 |
6 |
2 |
5 |
8 |
7 |
3 |
|
New Program |
9 |
9 |
7 |
8 |
10 |
9 |
6 |
|
Is there statistical evidence of a difference in APGAR scores in women receiving the new and enhanced versus usual prenatal care? We run the test using the five-step approach.
H0: The two populations are equal versus
H1: The two populations are not equal. α =0.05
Because APGAR scores are not normally distributed and the samples are small (n1=8 and n2=7), we use the Mann Whitney U test. The test statistic is U, the smaller of
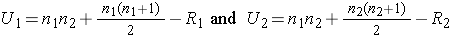
where R1 and R2 are the sums of the ranks in groups 1 and 2, respectively.
The appropriate critical value can be found in the table above. To determine the appropriate critical value we need sample sizes (n1=8 and n2=7) and our two-sided level of significance (α=0.05). The critical value for this test with n1=8, n2=7 and α =0.05 is 10 and the decision rule is as follows: Reject H0 if U < 10.
The first step is to assign ranks of 1 through 15 to the smallest through largest values in the total sample, as follows:
|
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||
|---|---|---|---|---|---|
|
Usual Care |
New Program |
Usual Care |
New Program |
Usual Care |
New Program |
|
8 |
9 |
2 |
|
1 |
|
|
7 |
8 |
3 |
|
2 |
|
|
6 |
7 |
5 |
|
3 |
|
|
2 |
8 |
6 |
6 |
4.5 |
4.5 |
|
5 |
10 |
7 |
7 |
7 |
7 |
|
8 |
9 |
7 |
|
7 |
|
|
7 |
6 |
8 |
8 |
10.5 |
10.5 |
|
3 |
|
8 |
8 |
10.5 |
10.5 |
|
|
|
|
9 |
|
13.5 |
|
|
|
|
9 |
|
13.5 |
|
|
|
|
10 |
|
15 |
|
|
|
|
|
R1=45.5 |
R2=74.5 |
Next, we sum the ranks in each group. In the usual care group, the sum of the ranks is R1=45.5 and in the new program group, the sum of the ranks is R2=74.5. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 15(16)/2=120 which is equal to 45.5+74.5 = 120.
We now compute U1 and U2, as follows:
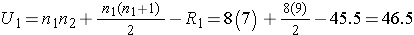
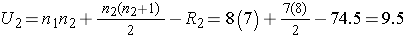
Thus, the test statistic is U=9.5.
We reject H0 because 9.5 < 10. We have statistically significant evidence at α =0.05 to show that the populations of APGAR scores are not equal in women receiving usual prenatal care as compared to the new program of prenatal care.
Example:
A clinical trial is run to assess the effectiveness of a new anti-retroviral therapy for patients with HIV. Patients are randomized to receive a standard anti-retroviral therapy (usual care) or the new anti-retroviral therapy and are monitored for 3 months. The primary outcome is viral load which represents the number of HIV copies per milliliter of blood. A total of 30 participants are randomized and the data are shown below.
|
Standard Therapy |
7500 |
8000 |
2000 |
550 |
1250 |
1000 |
2250 |
6800 |
3400 |
6300 |
9100 |
970 |
1040 |
670 |
400 |
|
New Therapy |
400 |
250 |
800 |
1400 |
8000 |
7400 |
1020 |
6000 |
920 |
1420 |
2700 |
4200 |
5200 |
4100 |
undetectable |
Is there statistical evidence of a difference in viral load in patients receiving the standard versus the new anti-retroviral therapy?
H0: The two populations are equal versus
H1: The two populations are not equal. α=0.05
Because viral load measures are not normally distributed (with outliers as well as limits of detection (e.g., "undetectable")), we use the Mann-Whitney U test. The test statistic is U, the smaller of
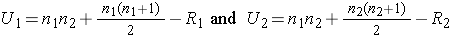
where R1 and R2 are the sums of the ranks in groups 1 and 2, respectively.
The critical value can be found in the table of critical values based on sample sizes (n1=n2=15) and a two-sided level of significance (α=0.05). The critical value 64 and the decision rule is as follows: Reject H0 if U < 64.
The first step is to assign ranks of 1 through 30 to the smallest through largest values in the total sample. Note in the table below, that the "undetectable" measurement is listed first in the ordered values (smallest) and assigned a rank of 1.
|
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||
|---|---|---|---|---|---|
|
Standard Anti-retroviral |
New Anti-retroviral |
Standard Anti-retroviral |
New Anti-retroviral |
Standard Anti-retroviral |
New Anti-retroviral |
|
7500 |
400 |
|
undetectable |
|
1 |
|
8000 |
250 |
|
250 |
|
2 |
|
2000 |
800 |
400 |
400 |
3.5 |
3.5 |
|
550 |
1400 |
550 |
|
5 |
|
|
1250 |
8000 |
670 |
|
6 |
|
|
1000 |
7400 |
|
800 |
|
7 |
|
2250 |
1020 |
|
920 |
|
8 |
|
6800 |
6000 |
970 |
|
9 |
|
|
3400 |
920 |
1000 |
|
10 |
|
|
6300 |
1420 |
|
1020 |
|
11 |
|
9100 |
2700 |
1040 |
|
12 |
|
|
970 |
4200 |
1250 |
|
13 |
|
|
1040 |
5200 |
|
1400 |
|
14 |
|
670 |
4100 |
|
1420 |
|
15 |
|
400 |
undetectable |
2000 |
|
16 |
|
|
|
|
2250 |
|
17 |
|
|
|
|
|
2700 |
|
18 |
|
|
|
3400 |
|
19 |
|
|
|
|
|
4100 |
|
20 |
|
|
|
|
4200 |
|
21 |
|
|
|
|
5200 |
|
22 |
|
|
|
|
6000 |
|
23 |
|
|
|
6300 |
|
24 |
|
|
|
|
6800 |
|
25 |
|
|
|
|
|
7400 |
|
26 |
|
|
|
7500 |
|
27 |
|
|
|
|
8000 |
8000 |
28.5 |
28.5 |
|
|
|
9100 |
|
30 |
|
|
|
|
|
|
R1 = 245 |
R2 = 220 |
Next, we sum the ranks in each group. In the standard anti-retroviral therapy group, the sum of the ranks is R1=245; in the new anti-retroviral therapy group, the sum of the ranks is R2=220. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 30(31)/2=465 which is equal to 245+220 = 465. We now compute U1 and U2, as follows,
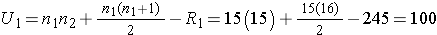
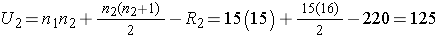
Thus, the test statistic is U=100.
We do not reject H0 because 100 > 64. We do not have sufficient evidence to conclude that the treatment groups differ in viral load.
This section describes nonparametric tests to compare two groups with respect to a continuous outcome when the data are collected on matched or paired samples. The parametric procedure for doing this was presented in the modules on hypothesis testing for the situation in which the continuous outcome was normally distributed. This section describes procedures that should be used when the outcome cannot be assumed to follow a normal distribution. There are two popular nonparametric tests to compare outcomes between two matched or paired groups. The first is called the Sign Test and the second the Wilcoxon Signed Rank Test.
Recall that when data are matched or paired, we compute difference scores for each individual and analyze difference scores. The same approach is followed in nonparametric tests. In parametric tests, the null hypothesis is that the mean difference (μd) is zero. In nonparametric tests, the null hypothesis is that the median difference is zero.
Example:
Consider a clinical investigation to assess the effectiveness of a new drug designed to reduce repetitive behaviors in children affected with autism. If the drug is effective, children will exhibit fewer repetitive behaviors on treatment as compared to when they are untreated. A total of 8 children with autism enroll in the study. Each child is observed by the study psychologist for a period of 3 hours both before treatment and then again after taking the new drug for 1 week. The time that each child is engaged in repetitive behavior during each 3 hour observation period is measured. Repetitive behavior is scored on a scale of 0 to 100 and scores represent the percent of the observation time in which the child is engaged in repetitive behavior. For example, a score of 0 indicates that during the entire observation period the child did not engage in repetitive behavior while a score of 100 indicates that the child was constantly engaged in repetitive behavior. The data are shown below.
|
Child |
Before Treatment |
After 1 Week of Treatment |
|---|---|---|
|
1 |
85 |
75 |
|
2 |
70 |
50 |
|
3 |
40 |
50 |
|
4 |
65 |
40 |
|
5 |
80 |
20 |
|
6 |
75 |
65 |
|
7 |
55 |
40 |
|
8 |
20 |
25 |
Looking at the data, it appears that some children improve (e.g., Child 5 scored 80 before treatment and 20 after treatment), but some got worse (e.g., Child 3 scored 40 before treatment and 50 after treatment). Is there statistically significant improvement in repetitive behavior after 1 week of treatment?.
Because the before and after treatment measures are paired, we compute difference scores for each child. In this example, we subtract the assessment of repetitive behaviors after treatment from that measured before treatment so that difference scores represent improvement in repetitive behavior. The question of interest is whether there is significant improvement after treatment.
|
Child |
Before Treatment |
After 1 Week of Treatment |
Difference (Before-After) |
|---|---|---|---|
|
1 |
85 |
75 |
10 |
|
2 |
70 |
50 |
20 |
|
3 |
40 |
50 |
-10 |
|
4 |
65 |
40 |
25 |
|
5 |
80 |
20 |
60 |
|
6 |
75 |
65 |
10 |
|
7 |
55 |
40 |
15 |
|
8 |
20 |
25 |
-5 |
In this small sample, the observed difference (or improvement) scores vary widely and are subject to extremes (e.g., the observed difference of 60 is an outlier). Thus, a nonparametric test is appropriate to test whether there is significant improvement in repetitive behavior before versus after treatment. The hypotheses are given below.
H0: The median difference is zero versus
H1: The median difference is positive α=0.05
In this example, the null hypothesis is that there is no difference in scores before versus after treatment. If the null hypothesis is true, we expect to see some positive differences (improvement) and some negative differences (worsening). If the research hypothesis is true, we expect to see more positive differences after treatment as compared to before.
The Sign Test is the simplest nonparametric test for matched or paired data. The approach is to analyze only the signs of the difference scores, as shown below:
|
Child |
Before Treatment |
After 1 Week of Treatment |
Difference (Before-After) |
Sign |
|---|---|---|---|---|
|
1 |
85 |
75 |
10 |
+ |
|
2 |
70 |
50 |
20 |
+ |
|
3 |
40 |
50 |
-10 |
- |
|
4 |
65 |
40 |
25 |
+ |
|
5 |
80 |
20 |
60 |
+ |
|
6 |
75 |
65 |
10 |
+ |
|
7 |
55 |
40 |
15 |
+ |
|
8 |
20 |
25 |
-5 |
- |
If the null hypothesis is true (i.e., if the median difference is zero) then we expect to see approximately half of the differences as positive and half of the differences as negative. If the research hypothesis is true, we expect to see more positive differences.
The test statistic for the Sign Test is the number of positive signs or number of negative signs, whichever is smaller. In this example, we observe 2 negative and 6 positive signs. Is this evidence of significant improvement or simply due to chance?
Determining whether the observed test statistic supports the null or research hypothesis is done following the same approach used in parametric testing. Specifically, we determine a critical value such that if the smaller of the number of positive or negative signs is less than or equal to that critical value, then we reject H0 in favor of H1 and if the smaller of the number of positive or negative signs is greater than the critical value, then we do not reject H0. Notice that this is a one-sided decision rule corresponding to our one-sided research hypothesis (the two-sided situation is discussed in the next example).
The critical values for the Sign Test are in the table below.
To determine the appropriate critical value we need the sample size, which is equal to the number of matched pairs (n=8) and our one-sided level of significance α=0.05. For this example, the critical value is 1, and the decision rule is to reject H0 if the smaller of the number of positive or negative signs < 1. We do not reject H0 because 2 > 1. We do not have sufficient evidence at α=0.05 to show that there is improvement in repetitive behavior after taking the drug as compared to before. In essence, we could use the critical value to decide whether to reject the null hypothesis. Another alternative would be to calculate the p-value, as described below.
With the Sign test we can readily compute a p-value based on our observed test statistic. The test statistic for the Sign Test is the smaller of the number of positive or negative signs and it follows a binomial distribution with n = the number of subjects in the study and p=0.5 (See the module on Probability for details on the binomial distribution). In the example above, n=8 and p=0.5 (the probability of success under H0).
By using the binomial distribution formula:
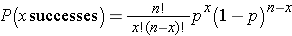
we can compute the probability of observing different numbers of successes during 8 trials. These are shown in the table below.
|
x=Number of Successes |
P(x successes) |
|---|---|
|
0 |
0.0039 |
|
1 |
0.0313 |
|
2 |
0.1094 |
|
3 |
0.2188 |
|
4 |
0.2734 |
|
5 |
0.2188 |
|
6 |
0.1094 |
|
7 |
0.0313 |
|
8 |
0.0039 |
Recall that a p-value is the probability of observing a test statistic as or more extreme than that observed. We observed 2 negative signs. Thus, the p-value for the test is: p-value = P(x < 2). Using the table above,
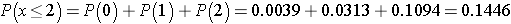
Because the p-value = 0.1446 exceeds the level of significance α=0.05, we do not have statistically significant evidence that there is improvement in repetitive behaviors after taking the drug as compared to before. Notice in the table of binomial probabilities above, that we would have had to observe at most 1 negative sign to declare statistical significance using a 5% level of significance. Recall the critical value for our test was 1 based on the table of critical values for the Sign Test (above).
In the example looking for differences in repetitive behaviors in autistic children, we used a one-sided test (i.e., we hypothesize improvement after taking the drug). A two sided test can be used if we hypothesize a difference in repetitive behavior after taking the drug as compared to before. From the table of critical values for the Sign Test, we can determine a two-sided critical value and again reject H0 if the smaller of the number of positive or negative signs is less than or equal to that two-sided critical value. Alternatively, we can compute a two-sided p-value. With a two-sided test, the p-value is the probability of observing many or few positive or negative signs. If the research hypothesis is a two sided alternative (i.e., H1: The median difference is not zero), then the p-value is computed as: p-value = 2*P(x < 2). Notice that this is equivalent to p-value = P(x < 2) + P(x > 6), representing the situation of few or many successes. Recall in two-sided tests, we reject the null hypothesis if the test statistic is extreme in either direction. Thus, in the Sign Test, a two-sided p-value is the probability of observing few or many positive or negative signs. Here we observe 2 negative signs (and thus 6 positive signs). The opposite situation would be 6 negative signs (and thus 2 positive signs as n=8). The two-sided p-value is the probability of observing a test statistic as or more extreme in either direction (i.e.,
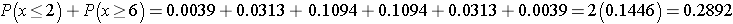
There is a special circumstance that needs attention when implementing the Sign Test which arises when one or more participants have difference scores of zero (i.e., their paired measurements are identical). If there is just one difference score of zero, some investigators drop that observation and reduce the sample size by 1 (i.e., the sample size for the binomial distribution would be n-1). This is a reasonable approach if there is just one zero. However, if there are two or more zeros, an alternative approach is preferred.
Example:
A new chemotherapy treatment is proposed for patients with breast cancer. Investigators are concerned with patient's ability to tolerate the treatment and assess their quality of life both before and after receiving the new chemotherapy treatment. Quality of life (QOL) is measured on an ordinal scale and for analysis purposes, numbers are assigned to each response category as follows: 1=Poor, 2= Fair, 3=Good, 4= Very Good, 5 = Excellent. The data are shown below.
|
Patient |
QOL Before Chemotherapy Treatment |
QOL After Chemotherapy Treatment |
|---|---|---|
|
1 |
3 |
2 |
|
2 |
2 |
3 |
|
3 |
3 |
4 |
|
4 |
2 |
4 |
|
5 |
1 |
1 |
|
6 |
3 |
4 |
|
7 |
2 |
4 |
|
8 |
3 |
3 |
|
9 |
2 |
1 |
|
10 |
1 |
3 |
|
11 |
3 |
4 |
|
12 |
2 |
3 |
The question of interest is whether there is a difference in QOL after chemotherapy treatment as compared to before.
H0: The median difference is zero versus
H1: The median difference is not zero α=0.05
The test statistic for the Sign Test is the smaller of the number of positive or negative signs.
The appropriate critical value for the Sign Test can be found in the table of critical values for the Sign Test. To determine the appropriate critical value we need the sample size (or number of matched pairs, n=12), and our two-sided level of significance α=0.05.
The critical value for this two-sided test with n=12 and a =0.05 is 2, and the decision rule is as follows: Reject H0 if the smaller of the number of positive or negative signs < 2.
Because the before and after treatment measures are paired, we compute difference scores for each patient. In this example, we subtract the QOL measured before treatment from that measured after.
|
Patient |
QOL Before Chemotherapy Treatment |
QOL After Chemotherapy Treatment |
Difference (After-Before) |
|---|---|---|---|
|
1 |
3 |
2 |
-1 |
|
2 |
2 |
3 |
1 |
|
3 |
3 |
4 |
1 |
|
4 |
2 |
4 |
2 |
|
5 |
1 |
1 |
0 |
|
6 |
3 |
4 |
1 |
|
7 |
2 |
4 |
2 |
|
8 |
3 |
3 |
0 |
|
9 |
2 |
1 |
-1 |
|
10 |
1 |
3 |
2 |
|
11 |
3 |
4 |
1 |
|
12 |
2 |
3 |
1 |
We now capture the signs of the difference scores and because there are two zeros, we randomly assign one negative sign (i.e., "-" to patient 5) and one positive sign (i.e., "+" to patient 8), as follows:
|
Patient |
QOL Before Chemotherapy Treatment |
QOL After Chemotherapy Treatment |
Difference (After-Before) |
Sign |
|---|---|---|---|---|
|
1 |
3 |
2 |
-1 |
- |
|
2 |
2 |
3 |
1 |
+ |
|
3 |
3 |
4 |
1 |
+ |
|
4 |
2 |
4 |
2 |
+ |
|
5 |
1 |
1 |
0 |
- |
|
6 |
3 |
4 |
1 |
+ |
|
7 |
2 |
4 |
2 |
+ |
|
8 |
3 |
3 |
0 |
+ |
|
9 |
2 |
1 |
-1 |
- |
|
10 |
1 |
3 |
2 |
+ |
|
11 |
3 |
4 |
1 |
+ |
|
12 |
2 |
3 |
1 |
+ |
The test statistic is the number of negative signs which is equal to 3.
We do not reject H0 because 3 > 2. We do not have statistically significant evidence at α=0.05 to show that there is a difference in QOL after chemotherapy treatment as compared to before.
We can also compute the p-value directly using the binomial distribution with n = 12 and p=0.5. The two-sided p-value for the test is p-value = 2*P(x < 3) (which is equivalent to p-value = P(x < 3) + P(x > 9)). Again, the two-sided p-value is the probability of observing few or many positive or negative signs. Here we observe 3 negative signs (and thus 9 positive signs). The opposite situation would be 9 negative signs (and thus 3 positive signs as n=12). The two-sided p-value is the probability of observing a test statistic as or more extreme in either direction (i.e., P(x < 3) + P(x > 9)). We can compute the p-value using the binomial formula or a statistical computing package, as follows:
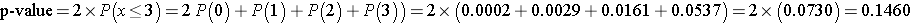
Because the p-value = 0.1460 exceeds the level of significance (α=0.05) we do not have statistically significant evidence at α =0.05 to show that there is a difference in QOL after chemotherapy treatment as compared to before.
|
Key Concept:
In each of the two previous examples, we failed to show statistical significance because the p-value was not less than the stated level of significance. While the test statistic for the Sign Test is easy to compute, it actually does not take much of the information in the sample data into account. All we measure is the difference in participant's scores, and do not account for the magnitude of those differences. |
Another popular nonparametric test for matched or paired data is called the Wilcoxon Signed Rank Test. Like the Sign Test, it is based on difference scores, but in addition to analyzing the signs of the differences, it also takes into account the magnitude of the observed differences.
Let's use the Wilcoxon Signed Rank Test to re-analyze the data in Example 4 on page 5 of this module. Recall that this study assessed the effectiveness of a new drug designed to reduce repetitive behaviors in children affected with autism. A total of 8 children with autism enroll in the study and the amount of time that each child is engaged in repetitive behavior during three hour observation periods are measured both before treatment and then again after taking the new medication for a period of 1 week. The data are shown below.
|
Child |
Before Treatment |
After 1 Week of Treatment |
|---|---|---|
|
1 |
85 |
75 |
|
2 |
70 |
50 |
|
3 |
40 |
50 |
|
4 |
65 |
40 |
|
5 |
80 |
20 |
|
6 |
75 |
65 |
|
7 |
55 |
40 |
|
8 |
20 |
25 |
First, we compute difference scores for each child.
|
Child |
Before Treatment |
After 1 Week of Treatment |
Difference (Before-After) |
|---|---|---|---|
|
1 |
85 |
75 |
10 |
|
2 |
70 |
50 |
20 |
|
3 |
40 |
50 |
-10 |
|
4 |
65 |
40 |
25 |
|
5 |
80 |
20 |
60 |
|
6 |
75 |
65 |
10 |
|
7 |
55 |
40 |
15 |
|
8 |
20 |
25 |
-5 |
The next step is to rank the difference scores. We first order the absolute values of the difference scores and assign rank from 1 through n to the smallest through largest absolute values of the difference scores, and assign the mean rank when there are ties in the absolute values of the difference scores.
|
Observed Differences |
|
Ordered Absolute Values of Differences |
Ranks |
|---|---|---|---|
|
10 |
|
-5 |
1 |
|
20 |
|
10 |
3 |
|
-10 |
|
-10 |
3 |
|
25 |
|
10 |
3 |
|
60 |
|
15 |
5 |
|
10 |
|
20 |
6 |
|
15 |
|
25 |
7 |
|
-5 |
|
60 |
8 |
The final step is to attach the signs ("+" or "-") of the observed differences to each rank as shown below.
|
Observed Differences |
|
Ordered Absolute Values of Difference Scores |
Ranks |
Signed Ranks |
|---|---|---|---|---|
|
10 |
|
-5 |
1 |
-1 |
|
20 |
|
10 |
3 |
3 |
|
-10 |
|
-10 |
3 |
-3 |
|
25 |
|
10 |
3 |
3 |
|
60 |
|
15 |
5 |
5 |
|
10 |
|
20 |
6 |
6 |
|
15 |
|
25 |
7 |
7 |
|
-5 |
|
60 |
8 |
8 |
Similar to the Sign Test, hypotheses for the Wilcoxon Signed Rank Test concern the population median of the difference scores. The research hypothesis can be one- or two-sided. Here we consider a one-sided test.
H0: The median difference is zero versus
H1: The median difference is positive α=0.05
The test statistic for the Wilcoxon Signed Rank Test is W, defined as the smaller of W+ (sum of the positive ranks) and W- (sum of the negative ranks). If the null hypothesis is true, we expect to see similar numbers of lower and higher ranks that are both positive and negative (i.e., W+ and W- would be similar). If the research hypothesis is true we expect to see more higher and positive ranks (in this example, more children with substantial improvement in repetitive behavior after treatment as compared to before, i.e., W+ much larger than W-).
In this example, W+ = 32 and W- = 4. Recall that the sum of the ranks (ignoring the signs) will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 8(9)/2 = 36 which is equal to 32+4. The test statistic is W = 4.
Next we must determine whether the observed test statistic W supports the null or research hypothesis. This is done following the same approach used in parametric testing. Specifically, we determine a critical value of W such that if the observed value of W is less than or equal to the critical value, we reject H0 in favor of H1, and if the observed value of W exceeds the critical value, we do not reject H0.
The critical value of W can be found in the table below:
To determine the appropriate one-sided critical value we need sample size (n=8) and our one-sided level of significance (α=0.05). For this example, the critical value of W is 6 and the decision rule is to reject H0 if W < 6. Thus, we reject H0, because 4 < 6. We have statistically significant evidence at α =0.05, to show that the median difference is positive (i.e., that repetitive behavior improves.)
Note that when we analyzed the data previously using the Sign Test, we failed to find statistical significance. However, when we use the Wilcoxon Signed Rank Test, we conclude that the treatment result in a statistically significant improvement at α=0.05. The discrepant results are due to the fact that the Sign Test uses very little information in the data and is a less powerful test.
Example:
A study is run to evaluate the effectiveness of an exercise program in reducing systolic blood pressure in patients with pre-hypertension (defined as a systolic blood pressure between 120-139 mmHg or a diastolic blood pressure between 80-89 mmHg). A total of 15 patients with pre-hypertension enroll in the study, and their systolic blood pressures are measured. Each patient then participates in an exercise training program where they learn proper techniques and execution of a series of exercises. Patients are instructed to do the exercise program 3 times per week for 6 weeks. After 6 weeks, systolic blood pressures are again measured. The data are shown below.
|
Patient |
Systolic Blood Pressure Before Exercise Program |
Systolic Blood Pressure After Exercise Program |
|---|---|---|
|
1 |
125 |
118 |
|
2 |
132 |
134 |
|
3 |
138 |
130 |
|
4 |
120 |
124 |
|
5 |
125 |
105 |
|
6 |
127 |
130 |
|
7 |
136 |
130 |
|
8 |
139 |
132 |
|
9 |
131 |
123 |
|
10 |
132 |
128 |
|
11 |
135 |
126 |
|
12 |
136 |
140 |
|
13 |
128 |
135 |
|
14 |
127 |
126 |
|
15 |
130 |
132 |
Is there is a difference in systolic blood pressures after participating in the exercise program as compared to before?
H0: The median difference is zero versus
H1: The median difference is not zero α=0.05
The test statistic for the Wilcoxon Signed Rank Test is W, defined as the smaller of W+ and W- which are the sums of the positive and negative ranks, respectively.
The critical value of W can be found in the table of critical values. To determine the appropriate critical value from Table 7 we need sample size (n=15) and our two-sided level of significance (α=0.05). The critical value for this two-sided test with n=15 and α=0.05 is 25 and the decision rule is as follows: Reject H0 if W < 25.
Because the before and after systolic blood pressures measures are paired, we compute difference scores for each patient.
Patient |
Systolic Blood Pressure Before Exercise Program |
Systolic Blood Pressure After Exercise Program |
Difference (Before-After) |
|---|---|---|---|
|
1 |
125 |
118 |
7 |
|
2 |
132 |
134 |
-2 |
|
3 |
138 |
130 |
8 |
|
4 |
120 |
124 |
-4 |
|
5 |
125 |
105 |
20 |
|
6 |
127 |
130 |
-3 |
|
7 |
136 |
130 |
6 |
|
8 |
139 |
132 |
7 |
|
9 |
131 |
123 |
8 |
|
10 |
132 |
128 |
4 |
|
11 |
135 |
126 |
9 |
|
12 |
136 |
140 |
-4 |
|
13 |
128 |
135 |
-7 |
|
14 |
127 |
126 |
1 |
|
15 |
130 |
132 |
-2 |
The next step is to rank the ordered absolute values of the difference scores using the approach outlined in Section 10.1. Specifically, we assign ranks from 1 through n to the smallest through largest absolute values of the difference scores, respectively, and assign the mean rank when there are ties in the absolute values of the difference scores.
|
Observed Differences |
|
Ordered Absolute Values of Differences |
Ranks |
|---|---|---|---|
|
7 |
|
1 |
1 |
|
-2 |
|
-2 |
2.5 |
|
8 |
|
-2 |
2.5 |
|
-4 |
|
-3 |
4 |
|
20 |
|
-4 |
6 |
|
-3 |
|
-4 |
6 |
|
6 |
|
4 |
6 |
|
7 |
|
6 |
8 |
|
8 |
|
-7 |
10 |
|
4 |
|
7 |
10 |
|
9 |
|
7 |
10 |
|
-4 |
|
8 |
12.5 |
|
-7 |
|
8 |
12.5 |
|
1 |
|
9 |
14 |
|
-2 |
|
20 |
15 |
The final step is to attach the signs ("+" or "-") of the observed differences to each rank as shown below.
|
Observed Differences |
|
Ordered Absolute Values of Differences |
Ranks |
Signed Ranks |
|---|---|---|---|---|
|
7 |
|
1 |
1 |
1 |
|
-2 |
|
-2 |
2.5 |
-2.5 |
|
8 |
|
-2 |
2.5 |
-2.5 |
|
-4 |
|
-3 |
4 |
-4 |
|
20 |
|
-4 |
6 |
-6 |
|
-3 |
|
-4 |
6 |
-6 |
|
6 |
|
4 |
6 |
6 |
|
7 |
|
6 |
8 |
8 |
|
8 |
|
-7 |
10 |
-10 |
|
4 |
|
7 |
10 |
10 |
In this example, W+ = 89 and W- = 31. Recall that the sum of the ranks (ignoring the signs) will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 15(16)/2 = 120 which is equal to 89 + 31. The test statistic is W = 31.
We do not reject H0 because 31 > 25. Therefore, we do not have statistically significant evidence at α=0.05, to show that the median difference in systolic blood pressures is not zero (i.e., that there is a significant difference in systolic blood pressures after the exercise program as compared to before).
In the modules on hypothesis testing we presented techniques for testing the equality of means in more than two independent samples using analysis of variance (ANOVA). An underlying assumption for appropriate use of ANOVA was that the continuous outcome was approximately normally distributed or that the samples were sufficiently large (usually nj> 30, where j=1, 2, ..., k and k denotes the number of independent comparison groups). An additional assumption for appropriate use of ANOVA is equality of variances in the k comparison groups. ANOVA is generally robust when the sample sizes are small but equal. When the outcome is not normally distributed and the samples are small, a nonparametric test is appropriate.
A popular nonparametric test to compare outcomes among more than two independent groups is the Kruskal Wallis test. The Kruskal Wallis test is used to compare medians among k comparison groups (k > 2) and is sometimes described as an ANOVA with the data replaced by their ranks. The null and research hypotheses for the Kruskal Wallis nonparametric test are stated as follows:
H0: The k population medians are equal versus
H1: The k population medians are not all equal
The procedure for the test involves pooling the observations from the k samples into one combined sample, keeping track of which sample each observation comes from, and then ranking lowest to highest from 1 to N, where N = n1+n2 + ...+ nk. To illustrate the procedure, consider the following example.
Example:
A clinical study is designed to assess differences in albumin levels in adults following diets with different amounts of protein. Low protein diets are often prescribed for patients with kidney failure. Albumin is the most abundant protein in blood, and its concentration in the serum is measured in grams per deciliter (g/dL). Clinically, serum albumin concentrations are also used to assess whether patients get sufficient protein in their diets. Three diets are compared, ranging from 5% to 15% protein, and the 15% protein diet represents a typical American diet. The albumin levels of participants following each diet are shown below.
|
5% Protein |
10% Protein |
15% Protein |
|---|---|---|
|
3.1 |
3.8 |
4.0 |
|
2.6 |
4.1 |
5.5 |
|
2.9 |
2.9 |
5.0 |
|
|
3.4 |
4.8 |
|
|
4.2 |
|
Is there is a difference in serum albumin levels among subjects on the three different diets. For reference, normal albumin levels are generally between 3.4 and 5.4 g/dL. By inspection, it appears that participants following the 15% protein diet have higher albumin levels than those following the 5% protein diet. The issue is whether this observed difference is statistically significant.
In this example, the outcome is continuous, but the sample sizes are small and not equal across comparison groups (n1=3, n2=5, n3=4). Thus, a nonparametric test is appropriate. The hypotheses to be tested are given below, and we will us a 5% level of significance.
H0: The three population medians are equal versus
H1: The three population medians are not all equal
To conduct the test we first order the data in the combined total sample of 12 subjects from smallest to largest. We also need to keep track of the group assignments in the total sample.
|
|
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||||
|---|---|---|---|---|---|---|---|---|
|
5% Protein |
10% Protein |
15% Protein |
5% Protein |
10% Protein |
15% Protein |
5% Protein |
10% Protein |
15% Protein |
|
3.1 |
3.8 |
4.0 |
2.6 |
|
|
1 |
|
|
|
2.6 |
4.1 |
5.5 |
2.9 |
2.9 |
|
2.5 |
2.5 |
|
|
2.9 |
2.9 |
5.0 |
3.1 |
|
|
4 |
|
|
|
|
3.4 |
4.8 |
|
3.4 |
|
|
5 |
|
|
|
4.2 |
|
|
3.8 |
|
|
6 |
|
|
|
|
|
|
|
4.0 |
|
|
7 |
|
|
|
|
|
4.1 |
|
|
8 |
|
|
|
|
|
|
4.2 |
|
|
9 |
|
|
|
|
|
|
|
4.8 |
|
|
10 |
|
|
|
|
|
|
5.0 |
|
|
11 |
|
|
|
|
|
|
5.5 |
|
|
12 |
Notice that the lower ranks (e.g., 1, 2.5, 4) are assigned to the 5% protein diet group while the higher ranks (e.g., 10, 11 and 12) are assigned to the 15% protein diet group. Again, the goal of the test is to determine whether the observed data support a difference in the three population medians. Recall in the parametric tests, discussed in the modules on hypothesis testing, when comparing means among more than two groups we analyzed the difference among the sample means (mean square between groups) relative to their within group variability and summarized the sample information in a test statistic (F statistic). In the Kruskal Wallis test we again summarize the sample information in a test statistic based on the ranks.
The test statistic for the Kruskal Wallis test is denoted H and is defined as follows:
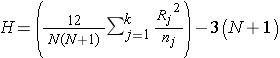
where k=the number of comparison groups, N= the total sample size, nj is the sample size in the jth group and Rj is the sum of the ranks in the jth group.
In this example R1 = 7.5, R2 = 30.5, and R3 = 40. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 12(13)/2=78 which is equal to 7.5+30.5+40 = 78. The H statistic for this example is computed as follows:
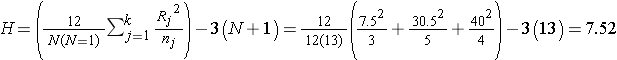 .
.
We must now determine whether the observed test statistic H supports the null or research hypothesis. Once again, this is done by establishing a critical value of H. If the observed value of H is greater than or equal to the critical value, we reject H0 in favor of H1; if the observed value of H is less than the critical value we do not reject H0. The critical value of H can be found in the table below.
To determine the appropriate critical value we need sample sizes (n1=3, n2=5 and n3=4) and our level of significance (α=0.05). For this example the critical value is 5.656, thus we reject H0 because 7.52 > 5.656, and we conclude that there is a difference in median albumin levels among the three different diets.
Notice that Table 8 contains critical values for the Kruskal Wallis test for tests comparing 3, 4 or 5 groups with small sample sizes. If there are 3 or more comparison groups and 5 or more observations in each of the comparison groups, it can be shown that the test statistic H approximates a chi-square distribution with df=k-1.4 Thus, in a Kruskal Wallis test with 3 or more comparison groups and 5 or more observations in each group, the critical value for the test can be found in the table of Critical Values of the χ 2 Distribution below.
The following example illustrates this situation.
Example:
A personal trainer is interested in comparing the anaerobic thresholds of elite athletes. Anaerobic threshold is defined as the point at which the muscles cannot get more oxygen to sustain activity or the upper limit of aerobic exercise. It is a measure also related to maximum heart rate. The following data are anaerobic thresholds for distance runners, distance cyclists, distance swimmers and cross-country skiers.
|
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
|---|---|---|---|
|
185 |
190 |
166 |
201 |
|
179 |
209 |
159 |
195 |
|
192 |
182 |
170 |
180 |
|
165 |
178 |
183 |
187 |
|
174 |
181 |
160 |
215 |
Is a difference in anaerobic thresholds among the different groups of elite athletes?
H0: The four population medians are equal versus
H1: The four population medians are not all equal α=0.05
The test statistic for the Kruskal Wallis test is denoted H and is defined as follows:
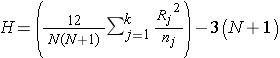 ,
,
where k=the number of comparison groups, N= the total sample size, nj is the sample size in the jth group and Rj is the sum of the ranks in the jth group.
Because there are 4 comparison groups and 5 observations in each of the comparison groups, we find the critical value in the table of critical values for the chi-square distribution for df=k-1=4-1=3 and α=0.05. The critical value is 7.81, and the decision rule is to reject H0 if H > 7.81.
To conduct the test we assign ranks using the procedures outlined above. The first step in assigning ranks is to order the data from smallest to largest. This is done on the combined or total sample (i.e., pooling the data from the four comparison groups (n=20)), and assigning ranks from 1 to 20, as follows. We also need to keep track of the group assignments in the total sample. The table below shows the ordered data.
|
|
|
|
|
Total Sample (Ordered Smallest to Largest) |
|||
|---|---|---|---|---|---|---|---|
|
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
|
185 |
190 |
166 |
201 |
|
|
159 |
|
|
179 |
209 |
159 |
195 |
|
|
160 |
|
|
192 |
182 |
170 |
180 |
165 |
|
|
|
|
165 |
178 |
183 |
187 |
|
|
166 |
|
|
174 |
181 |
160 |
215 |
|
|
170 |
|
|
|
|
|
|
174 |
|
|
|
|
|
|
|
|
|
178 |
|
|
|
|
|
|
|
179 |
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
181 |
|
|
|
|
|
|
|
|
182 |
|
|
|
|
|
|
|
|
|
183 |
|
|
|
|
|
|
185 |
|
|
|
|
|
|
|
|
|
|
|
187 |
|
|
|
|
|
|
190 |
|
|
|
|
|
|
|
192 |
|
|
|
|
|
|
|
|
|
|
|
195 |
|
|
|
|
|
|
|
|
201 |
|
|
|
|
|
|
209 |
|
|
|
|
|
|
|
|
|
|
215 |
We now assign the ranks to the ordered values and sum the ranks in each group.
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||||||
|---|---|---|---|---|---|---|---|
|
Distance Runners |
Distance Runners |
Distance Runners |
Distance Runners |
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
|
|
|
159 |
|
|
|
1 |
|
|
|
|
160 |
|
|
|
2 |
|
|
165 |
|
|
|
3 |
|
|
|
|
|
|
166 |
|
|
|
4 |
|
|
|
|
170 |
|
|
|
5 |
|
|
174 |
|
|
|
6 |
|
|
|
|
|
178 |
|
|
|
7 |
|
|
|
179 |
|
|
|
8 |
|
|
|
|
|
|
|
180 |
|
|
|
9 |
|
|
181 |
|
|
|
10 |
|
|
|
|
182 |
|
|
|
11 |
|
|
|
|
|
183 |
|
|
|
12 |
|
|
185 |
|
|
|
13 |
|
|
|
|
|
|
|
187 |
|
|
|
14 |
|
|
190 |
|
|
|
15 |
|
|
|
192 |
|
|
|
16 |
|
|
|
|
|
|
|
195 |
|
|
|
17 |
|
|
|
|
201 |
|
|
|
18 |
|
|
209 |
|
|
|
19 |
|
|
|
|
|
|
215 |
|
|
|
20 |
|
|
|
|
|
R1=46 |
R2=62 |
R3=24 |
R4=78 |
Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 20(21)/2=210 which is equal to 46+62+24+78 = 210. In this example,
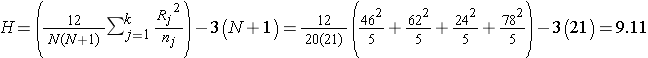 .
.
Reject H0 because 9.11 > 7.81. We have statistically significant evidence at α =0.05, to show that there is a difference in median anaerobic thresholds among the four different groups of elite athletes.
Notice that in this example, the anaerobic thresholds of the distance runners, cyclists and cross-country skiers are comparable (looking only at the raw data). The distance swimmers appear to be the athletes that differ from the others in terms of anaerobic thresholds. Recall, similar to analysis of variance tests, we reject the null hypothesis in favor of the alternative hypothesis if any two of the medians are not equal.
This module presents hypothesis testing techniques for situations with small sample sizes and outcomes that are ordinal, ranked or continuous and cannot be assumed to be normally distributed. Nonparametric tests are based on ranks which are assigned to the ordered data. The tests involve the same five steps as parametric tests, specifying the null and alternative or research hypothesis, selecting and computing an appropriate test statistic, setting up a decision rule and drawing a conclusion. The tests are summarized below.
Use: To compare a continuous outcome in two independent samples.
Null Hypothesis: H0: Two populations are equal
Test Statistic: The test statistic is U, the smaller of
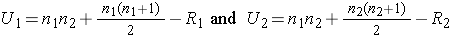
where R1 and R2 are the sums of the ranks in groups 1 and 2, respectively.
Decision Rule: Reject H0 if U < critical value from table
Use: To compare a continuous outcome in two matched or paired samples.
Null Hypothesis: H0: Median difference is zero
Test Statistic: The test statistic is the smaller of the number of positive or negative signs.
Decision Rule: Reject H0 if the smaller of the number of positive or negative signs < critical value from table.
Use: To compare a continuous outcome in two matched or paired samples.
Null Hypothesis: H0: Median difference is zero
Test Statistic: The test statistic is W, defined as the smaller of W+ and W- which are the sums of the positive and negative ranks of the difference scores, respectively.
Decision Rule: Reject H0 if W < critical value from table.
Use: To compare a continuous outcome in more than two independent samples.
Null Hypothesis: H0: k population medians are equal
Test Statistic: The test statistic is H,
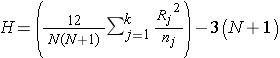
where k=the number of comparison groups, N= the total sample size, nj is the sample size in the jth group and Rj is the sum of the ranks in the jth group.
Decision Rule: Reject H0 if H > critical value
|
Key Concept: It is important to note that nonparametric tests are subject to the same errors as parametric tests. A Type I error occurs when a test incorrectly rejects the null hypothesis. A Type II error occurs when a test fails to reject H0 when it is false. Power is the probability of a test to correctly reject H0. Nonparametric tests can be subject to low power mainly due to small sample size. Therefore, it is important to consider the possibility of a Type II error when a nonparametric test fails to reject H0. There may be a true effect or difference, yet the nonparametric test is underpowered to detect it. For more details, interested readers should see Conover and Siegel and Castellan.3,4
|