Tests with More than Two Independent Samples
In the modules on hypothesis testing we presented techniques for testing the equality of means in more than two independent samples using analysis of variance (ANOVA). An underlying assumption for appropriate use of ANOVA was that the continuous outcome was approximately normally distributed or that the samples were sufficiently large (usually nj> 30, where j=1, 2, ..., k and k denotes the number of independent comparison groups). An additional assumption for appropriate use of ANOVA is equality of variances in the k comparison groups. ANOVA is generally robust when the sample sizes are small but equal. When the outcome is not normally distributed and the samples are small, a nonparametric test is appropriate.
The Kruskal-Wallis Test
A popular nonparametric test to compare outcomes among more than two independent groups is the Kruskal Wallis test. The Kruskal Wallis test is used to compare medians among k comparison groups (k > 2) and is sometimes described as an ANOVA with the data replaced by their ranks. The null and research hypotheses for the Kruskal Wallis nonparametric test are stated as follows:
H0: The k population medians are equal versus
H1: The k population medians are not all equal
The procedure for the test involves pooling the observations from the k samples into one combined sample, keeping track of which sample each observation comes from, and then ranking lowest to highest from 1 to N, where N = n1+n2 + ...+ nk. To illustrate the procedure, consider the following example.
Example:
A clinical study is designed to assess differences in albumin levels in adults following diets with different amounts of protein. Low protein diets are often prescribed for patients with kidney failure. Albumin is the most abundant protein in blood, and its concentration in the serum is measured in grams per deciliter (g/dL). Clinically, serum albumin concentrations are also used to assess whether patients get sufficient protein in their diets. Three diets are compared, ranging from 5% to 15% protein, and the 15% protein diet represents a typical American diet. The albumin levels of participants following each diet are shown below.
|
5% Protein |
10% Protein |
15% Protein |
|---|---|---|
|
3.1 |
3.8 |
4.0 |
|
2.6 |
4.1 |
5.5 |
|
2.9 |
2.9 |
5.0 |
|
|
3.4 |
4.8 |
|
|
4.2 |
|
Is there is a difference in serum albumin levels among subjects on the three different diets. For reference, normal albumin levels are generally between 3.4 and 5.4 g/dL. By inspection, it appears that participants following the 15% protein diet have higher albumin levels than those following the 5% protein diet. The issue is whether this observed difference is statistically significant.
In this example, the outcome is continuous, but the sample sizes are small and not equal across comparison groups (n1=3, n2=5, n3=4). Thus, a nonparametric test is appropriate. The hypotheses to be tested are given below, and we will us a 5% level of significance.
H0: The three population medians are equal versus
H1: The three population medians are not all equal
To conduct the test we first order the data in the combined total sample of 12 subjects from smallest to largest. We also need to keep track of the group assignments in the total sample.
|
|
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||||
|---|---|---|---|---|---|---|---|---|
|
5% Protein |
10% Protein |
15% Protein |
5% Protein |
10% Protein |
15% Protein |
5% Protein |
10% Protein |
15% Protein |
|
3.1 |
3.8 |
4.0 |
2.6 |
|
|
1 |
|
|
|
2.6 |
4.1 |
5.5 |
2.9 |
2.9 |
|
2.5 |
2.5 |
|
|
2.9 |
2.9 |
5.0 |
3.1 |
|
|
4 |
|
|
|
|
3.4 |
4.8 |
|
3.4 |
|
|
5 |
|
|
|
4.2 |
|
|
3.8 |
|
|
6 |
|
|
|
|
|
|
|
4.0 |
|
|
7 |
|
|
|
|
|
4.1 |
|
|
8 |
|
|
|
|
|
|
4.2 |
|
|
9 |
|
|
|
|
|
|
|
4.8 |
|
|
10 |
|
|
|
|
|
|
5.0 |
|
|
11 |
|
|
|
|
|
|
5.5 |
|
|
12 |
Notice that the lower ranks (e.g., 1, 2.5, 4) are assigned to the 5% protein diet group while the higher ranks (e.g., 10, 11 and 12) are assigned to the 15% protein diet group. Again, the goal of the test is to determine whether the observed data support a difference in the three population medians. Recall in the parametric tests, discussed in the modules on hypothesis testing, when comparing means among more than two groups we analyzed the difference among the sample means (mean square between groups) relative to their within group variability and summarized the sample information in a test statistic (F statistic). In the Kruskal Wallis test we again summarize the sample information in a test statistic based on the ranks.
Test Statistic for the Kruskal Wallis Test
The test statistic for the Kruskal Wallis test is denoted H and is defined as follows:

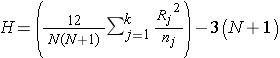
where k=the number of comparison groups, N= the total sample size, nj is the sample size in the jth group and Rj is the sum of the ranks in the jth group.
In this example R1 = 7.5, R2 = 30.5, and R3 = 40. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 12(13)/2=78 which is equal to 7.5+30.5+40 = 78. The H statistic for this example is computed as follows:

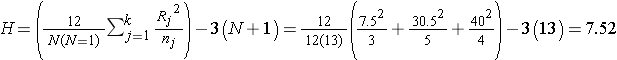 .
.
We must now determine whether the observed test statistic H supports the null or research hypothesis. Once again, this is done by establishing a critical value of H. If the observed value of H is greater than or equal to the critical value, we reject H0 in favor of H1; if the observed value of H is less than the critical value we do not reject H0. The critical value of H can be found in the table below.
Critical Values of H for the Kruskal Wallis Test
To determine the appropriate critical value we need sample sizes (n1=3, n2=5 and n3=4) and our level of significance (α=0.05). For this example the critical value is 5.656, thus we reject H0 because 7.52 > 5.656, and we conclude that there is a difference in median albumin levels among the three different diets.
Notice that Table 8 contains critical values for the Kruskal Wallis test for tests comparing 3, 4 or 5 groups with small sample sizes. If there are 3 or more comparison groups and 5 or more observations in each of the comparison groups, it can be shown that the test statistic H approximates a chi-square distribution with df=k-1.4 Thus, in a Kruskal Wallis test with 3 or more comparison groups and 5 or more observations in each group, the critical value for the test can be found in the table of Critical Values of the χ 2 Distribution below.
Critical Values of the χ2 Distribution
The following example illustrates this situation.
Example:
A personal trainer is interested in comparing the anaerobic thresholds of elite athletes. Anaerobic threshold is defined as the point at which the muscles cannot get more oxygen to sustain activity or the upper limit of aerobic exercise. It is a measure also related to maximum heart rate. The following data are anaerobic thresholds for distance runners, distance cyclists, distance swimmers and cross-country skiers.
|
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
|---|---|---|---|
|
185 |
190 |
166 |
201 |
|
179 |
209 |
159 |
195 |
|
192 |
182 |
170 |
180 |
|
165 |
178 |
183 |
187 |
|
174 |
181 |
160 |
215 |
Is a difference in anaerobic thresholds among the different groups of elite athletes?
- Step 1. Set up hypotheses and determine level of significance.
H0: The four population medians are equal versus
H1: The four population medians are not all equal α=0.05
- Step 2. Select the appropriate test statistic.
The test statistic for the Kruskal Wallis test is denoted H and is defined as follows:

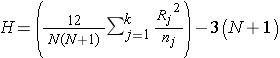 ,
,
where k=the number of comparison groups, N= the total sample size, nj is the sample size in the jth group and Rj is the sum of the ranks in the jth group.
- Step 3. Set up the decision rule.
Because there are 4 comparison groups and 5 observations in each of the comparison groups, we find the critical value in the table of critical values for the chi-square distribution for df=k-1=4-1=3 and α=0.05. The critical value is 7.81, and the decision rule is to reject H0 if H > 7.81.
- Step 4. Compute the test statistic.
To conduct the test we assign ranks using the procedures outlined above. The first step in assigning ranks is to order the data from smallest to largest. This is done on the combined or total sample (i.e., pooling the data from the four comparison groups (n=20)), and assigning ranks from 1 to 20, as follows. We also need to keep track of the group assignments in the total sample. The table below shows the ordered data.
|
|
|
|
|
Total Sample (Ordered Smallest to Largest) |
|||
|---|---|---|---|---|---|---|---|
|
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
|
185 |
190 |
166 |
201 |
|
|
159 |
|
|
179 |
209 |
159 |
195 |
|
|
160 |
|
|
192 |
182 |
170 |
180 |
165 |
|
|
|
|
165 |
178 |
183 |
187 |
|
|
166 |
|
|
174 |
181 |
160 |
215 |
|
|
170 |
|
|
|
|
|
|
174 |
|
|
|
|
|
|
|
|
|
178 |
|
|
|
|
|
|
|
179 |
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
181 |
|
|
|
|
|
|
|
|
182 |
|
|
|
|
|
|
|
|
|
183 |
|
|
|
|
|
|
185 |
|
|
|
|
|
|
|
|
|
|
|
187 |
|
|
|
|
|
|
190 |
|
|
|
|
|
|
|
192 |
|
|
|
|
|
|
|
|
|
|
|
195 |
|
|
|
|
|
|
|
|
201 |
|
|
|
|
|
|
209 |
|
|
|
|
|
|
|
|
|
|
215 |
We now assign the ranks to the ordered values and sum the ranks in each group.
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||||||
|---|---|---|---|---|---|---|---|
|
Distance Runners |
Distance Runners |
Distance Runners |
Distance Runners |
Distance Runners |
Distance Cyclists |
Distance Swimmers |
Cross-Country Skiers |
|
|
|
159 |
|
|
|
1 |
|
|
|
|
160 |
|
|
|
2 |
|
|
165 |
|
|
|
3 |
|
|
|
|
|
|
166 |
|
|
|
4 |
|
|
|
|
170 |
|
|
|
5 |
|
|
174 |
|
|
|
6 |
|
|
|
|
|
178 |
|
|
|
7 |
|
|
|
179 |
|
|
|
8 |
|
|
|
|
|
|
|
180 |
|
|
|
9 |
|
|
181 |
|
|
|
10 |
|
|
|
|
182 |
|
|
|
11 |
|
|
|
|
|
183 |
|
|
|
12 |
|
|
185 |
|
|
|
13 |
|
|
|
|
|
|
|
187 |
|
|
|
14 |
|
|
190 |
|
|
|
15 |
|
|
|
192 |
|
|
|
16 |
|
|
|
|
|
|
|
195 |
|
|
|
17 |
|
|
|
|
201 |
|
|
|
18 |
|
|
209 |
|
|
|
19 |
|
|
|
|
|
|
215 |
|
|
|
20 |
|
|
|
|
|
R1=46 |
R2=62 |
R3=24 |
R4=78 |
Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 20(21)/2=210 which is equal to 46+62+24+78 = 210. In this example,

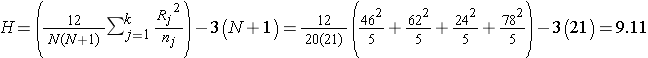 .
.
- Step 5. Conclusion.
Reject H0 because 9.11 > 7.81. We have statistically significant evidence at α =0.05, to show that there is a difference in median anaerobic thresholds among the four different groups of elite athletes.
Notice that in this example, the anaerobic thresholds of the distance runners, cyclists and cross-country skiers are comparable (looking only at the raw data). The distance swimmers appear to be the athletes that differ from the others in terms of anaerobic thresholds. Recall, similar to analysis of variance tests, we reject the null hypothesis in favor of the alternative hypothesis if any two of the medians are not equal.