Tests with Matched Samples
This section describes nonparametric tests to compare two groups with respect to a continuous outcome when the data are collected on matched or paired samples. The parametric procedure for doing this was presented in the modules on hypothesis testing for the situation in which the continuous outcome was normally distributed. This section describes procedures that should be used when the outcome cannot be assumed to follow a normal distribution. There are two popular nonparametric tests to compare outcomes between two matched or paired groups. The first is called the Sign Test and the second the Wilcoxon Signed Rank Test.
Recall that when data are matched or paired, we compute difference scores for each individual and analyze difference scores. The same approach is followed in nonparametric tests. In parametric tests, the null hypothesis is that the mean difference (μd) is zero. In nonparametric tests, the null hypothesis is that the median difference is zero.
Example:
Consider a clinical investigation to assess the effectiveness of a new drug designed to reduce repetitive behaviors in children affected with autism. If the drug is effective, children will exhibit fewer repetitive behaviors on treatment as compared to when they are untreated. A total of 8 children with autism enroll in the study. Each child is observed by the study psychologist for a period of 3 hours both before treatment and then again after taking the new drug for 1 week. The time that each child is engaged in repetitive behavior during each 3 hour observation period is measured. Repetitive behavior is scored on a scale of 0 to 100 and scores represent the percent of the observation time in which the child is engaged in repetitive behavior. For example, a score of 0 indicates that during the entire observation period the child did not engage in repetitive behavior while a score of 100 indicates that the child was constantly engaged in repetitive behavior. The data are shown below.
|
Child |
Before Treatment |
After 1 Week of Treatment |
|---|---|---|
|
1 |
85 |
75 |
|
2 |
70 |
50 |
|
3 |
40 |
50 |
|
4 |
65 |
40 |
|
5 |
80 |
20 |
|
6 |
75 |
65 |
|
7 |
55 |
40 |
|
8 |
20 |
25 |
Looking at the data, it appears that some children improve (e.g., Child 5 scored 80 before treatment and 20 after treatment), but some got worse (e.g., Child 3 scored 40 before treatment and 50 after treatment). Is there statistically significant improvement in repetitive behavior after 1 week of treatment?.
Because the before and after treatment measures are paired, we compute difference scores for each child. In this example, we subtract the assessment of repetitive behaviors after treatment from that measured before treatment so that difference scores represent improvement in repetitive behavior. The question of interest is whether there is significant improvement after treatment.
|
Child |
Before Treatment |
After 1 Week of Treatment |
Difference (Before-After) |
|---|---|---|---|
|
1 |
85 |
75 |
10 |
|
2 |
70 |
50 |
20 |
|
3 |
40 |
50 |
-10 |
|
4 |
65 |
40 |
25 |
|
5 |
80 |
20 |
60 |
|
6 |
75 |
65 |
10 |
|
7 |
55 |
40 |
15 |
|
8 |
20 |
25 |
-5 |
In this small sample, the observed difference (or improvement) scores vary widely and are subject to extremes (e.g., the observed difference of 60 is an outlier). Thus, a nonparametric test is appropriate to test whether there is significant improvement in repetitive behavior before versus after treatment. The hypotheses are given below.
H0: The median difference is zero versus
H1: The median difference is positive α=0.05
In this example, the null hypothesis is that there is no difference in scores before versus after treatment. If the null hypothesis is true, we expect to see some positive differences (improvement) and some negative differences (worsening). If the research hypothesis is true, we expect to see more positive differences after treatment as compared to before.
The Sign Test
The Sign Test is the simplest nonparametric test for matched or paired data. The approach is to analyze only the signs of the difference scores, as shown below:
|
Child |
Before Treatment |
After 1 Week of Treatment |
Difference (Before-After) |
Sign |
|---|---|---|---|---|
|
1 |
85 |
75 |
10 |
+ |
|
2 |
70 |
50 |
20 |
+ |
|
3 |
40 |
50 |
-10 |
- |
|
4 |
65 |
40 |
25 |
+ |
|
5 |
80 |
20 |
60 |
+ |
|
6 |
75 |
65 |
10 |
+ |
|
7 |
55 |
40 |
15 |
+ |
|
8 |
20 |
25 |
-5 |
- |
If the null hypothesis is true (i.e., if the median difference is zero) then we expect to see approximately half of the differences as positive and half of the differences as negative. If the research hypothesis is true, we expect to see more positive differences.
Test Statistic for the Sign Test
The test statistic for the Sign Test is the number of positive signs or number of negative signs, whichever is smaller. In this example, we observe 2 negative and 6 positive signs. Is this evidence of significant improvement or simply due to chance?
Determining whether the observed test statistic supports the null or research hypothesis is done following the same approach used in parametric testing. Specifically, we determine a critical value such that if the smaller of the number of positive or negative signs is less than or equal to that critical value, then we reject H0 in favor of H1 and if the smaller of the number of positive or negative signs is greater than the critical value, then we do not reject H0. Notice that this is a one-sided decision rule corresponding to our one-sided research hypothesis (the two-sided situation is discussed in the next example).
Table of Critical Values for the Sign Test
The critical values for the Sign Test are in the table below.
To determine the appropriate critical value we need the sample size, which is equal to the number of matched pairs (n=8) and our one-sided level of significance α=0.05. For this example, the critical value is 1, and the decision rule is to reject H0 if the smaller of the number of positive or negative signs < 1. We do not reject H0 because 2 > 1. We do not have sufficient evidence at α=0.05 to show that there is improvement in repetitive behavior after taking the drug as compared to before. In essence, we could use the critical value to decide whether to reject the null hypothesis. Another alternative would be to calculate the p-value, as described below.
Computing P-values for the Sign Test
With the Sign test we can readily compute a p-value based on our observed test statistic. The test statistic for the Sign Test is the smaller of the number of positive or negative signs and it follows a binomial distribution with n = the number of subjects in the study and p=0.5 (See the module on Probability for details on the binomial distribution). In the example above, n=8 and p=0.5 (the probability of success under H0).
By using the binomial distribution formula:

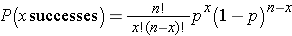
we can compute the probability of observing different numbers of successes during 8 trials. These are shown in the table below.
|
x=Number of Successes |
P(x successes) |
|---|---|
|
0 |
0.0039 |
|
1 |
0.0313 |
|
2 |
0.1094 |
|
3 |
0.2188 |
|
4 |
0.2734 |
|
5 |
0.2188 |
|
6 |
0.1094 |
|
7 |
0.0313 |
|
8 |
0.0039 |
Recall that a p-value is the probability of observing a test statistic as or more extreme than that observed. We observed 2 negative signs. Thus, the p-value for the test is: p-value = P(x < 2). Using the table above,

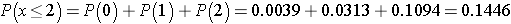
Because the p-value = 0.1446 exceeds the level of significance α=0.05, we do not have statistically significant evidence that there is improvement in repetitive behaviors after taking the drug as compared to before. Notice in the table of binomial probabilities above, that we would have had to observe at most 1 negative sign to declare statistical significance using a 5% level of significance. Recall the critical value for our test was 1 based on the table of critical values for the Sign Test (above).
One-Sided versus Two-Sided Test
In the example looking for differences in repetitive behaviors in autistic children, we used a one-sided test (i.e., we hypothesize improvement after taking the drug). A two sided test can be used if we hypothesize a difference in repetitive behavior after taking the drug as compared to before. From the table of critical values for the Sign Test, we can determine a two-sided critical value and again reject H0 if the smaller of the number of positive or negative signs is less than or equal to that two-sided critical value. Alternatively, we can compute a two-sided p-value. With a two-sided test, the p-value is the probability of observing many or few positive or negative signs. If the research hypothesis is a two sided alternative (i.e., H1: The median difference is not zero), then the p-value is computed as: p-value = 2*P(x < 2). Notice that this is equivalent to p-value = P(x < 2) + P(x > 6), representing the situation of few or many successes. Recall in two-sided tests, we reject the null hypothesis if the test statistic is extreme in either direction. Thus, in the Sign Test, a two-sided p-value is the probability of observing few or many positive or negative signs. Here we observe 2 negative signs (and thus 6 positive signs). The opposite situation would be 6 negative signs (and thus 2 positive signs as n=8). The two-sided p-value is the probability of observing a test statistic as or more extreme in either direction (i.e.,

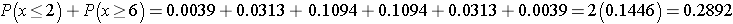
When Difference Scores are Zero
There is a special circumstance that needs attention when implementing the Sign Test which arises when one or more participants have difference scores of zero (i.e., their paired measurements are identical). If there is just one difference score of zero, some investigators drop that observation and reduce the sample size by 1 (i.e., the sample size for the binomial distribution would be n-1). This is a reasonable approach if there is just one zero. However, if there are two or more zeros, an alternative approach is preferred.
- If there is an even number of zeros, we randomly assign them positive or negative signs.
- If there is an odd number of zeros, we randomly drop one and reduce the sample size by 1, and then randomly assign the remaining observations positive or negative signs. The following example illustrates the approach.
Example:
A new chemotherapy treatment is proposed for patients with breast cancer. Investigators are concerned with patient's ability to tolerate the treatment and assess their quality of life both before and after receiving the new chemotherapy treatment. Quality of life (QOL) is measured on an ordinal scale and for analysis purposes, numbers are assigned to each response category as follows: 1=Poor, 2= Fair, 3=Good, 4= Very Good, 5 = Excellent. The data are shown below.
|
Patient |
QOL Before Chemotherapy Treatment |
QOL After Chemotherapy Treatment |
|---|---|---|
|
1 |
3 |
2 |
|
2 |
2 |
3 |
|
3 |
3 |
4 |
|
4 |
2 |
4 |
|
5 |
1 |
1 |
|
6 |
3 |
4 |
|
7 |
2 |
4 |
|
8 |
3 |
3 |
|
9 |
2 |
1 |
|
10 |
1 |
3 |
|
11 |
3 |
4 |
|
12 |
2 |
3 |
The question of interest is whether there is a difference in QOL after chemotherapy treatment as compared to before.
- Step 1. Set up hypotheses and determine level of significance.
H0: The median difference is zero versus
H1: The median difference is not zero α=0.05
- Step 2. Select the appropriate test statistic.
The test statistic for the Sign Test is the smaller of the number of positive or negative signs.
- Step 3. Set up the decision rule.
The appropriate critical value for the Sign Test can be found in the table of critical values for the Sign Test. To determine the appropriate critical value we need the sample size (or number of matched pairs, n=12), and our two-sided level of significance α=0.05.
The critical value for this two-sided test with n=12 and a =0.05 is 2, and the decision rule is as follows: Reject H0 if the smaller of the number of positive or negative signs < 2.
- Step 4. Compute the test statistic.
Because the before and after treatment measures are paired, we compute difference scores for each patient. In this example, we subtract the QOL measured before treatment from that measured after.
|
Patient |
QOL Before Chemotherapy Treatment |
QOL After Chemotherapy Treatment |
Difference (After-Before) |
|---|---|---|---|
|
1 |
3 |
2 |
-1 |
|
2 |
2 |
3 |
1 |
|
3 |
3 |
4 |
1 |
|
4 |
2 |
4 |
2 |
|
5 |
1 |
1 |
0 |
|
6 |
3 |
4 |
1 |
|
7 |
2 |
4 |
2 |
|
8 |
3 |
3 |
0 |
|
9 |
2 |
1 |
-1 |
|
10 |
1 |
3 |
2 |
|
11 |
3 |
4 |
1 |
|
12 |
2 |
3 |
1 |
We now capture the signs of the difference scores and because there are two zeros, we randomly assign one negative sign (i.e., "-" to patient 5) and one positive sign (i.e., "+" to patient 8), as follows:
|
Patient |
QOL Before Chemotherapy Treatment |
QOL After Chemotherapy Treatment |
Difference (After-Before) |
Sign |
|---|---|---|---|---|
|
1 |
3 |
2 |
-1 |
- |
|
2 |
2 |
3 |
1 |
+ |
|
3 |
3 |
4 |
1 |
+ |
|
4 |
2 |
4 |
2 |
+ |
|
5 |
1 |
1 |
0 |
- |
|
6 |
3 |
4 |
1 |
+ |
|
7 |
2 |
4 |
2 |
+ |
|
8 |
3 |
3 |
0 |
+ |
|
9 |
2 |
1 |
-1 |
- |
|
10 |
1 |
3 |
2 |
+ |
|
11 |
3 |
4 |
1 |
+ |
|
12 |
2 |
3 |
1 |
+ |
The test statistic is the number of negative signs which is equal to 3.
- Step 5. Conclusion.
We do not reject H0 because 3 > 2. We do not have statistically significant evidence at α=0.05 to show that there is a difference in QOL after chemotherapy treatment as compared to before.
We can also compute the p-value directly using the binomial distribution with n = 12 and p=0.5. The two-sided p-value for the test is p-value = 2*P(x < 3) (which is equivalent to p-value = P(x < 3) + P(x > 9)). Again, the two-sided p-value is the probability of observing few or many positive or negative signs. Here we observe 3 negative signs (and thus 9 positive signs). The opposite situation would be 9 negative signs (and thus 3 positive signs as n=12). The two-sided p-value is the probability of observing a test statistic as or more extreme in either direction (i.e., P(x < 3) + P(x > 9)). We can compute the p-value using the binomial formula or a statistical computing package, as follows:

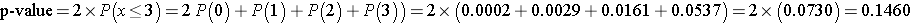
Because the p-value = 0.1460 exceeds the level of significance (α=0.05) we do not have statistically significant evidence at α =0.05 to show that there is a difference in QOL after chemotherapy treatment as compared to before.
|
Key Concept:
In each of the two previous examples, we failed to show statistical significance because the p-value was not less than the stated level of significance. While the test statistic for the Sign Test is easy to compute, it actually does not take much of the information in the sample data into account. All we measure is the difference in participant's scores, and do not account for the magnitude of those differences. |