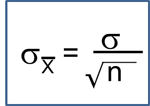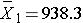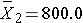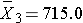Another ANOVA Example
Calcium is an essential mineral that regulates the heart, is important for blood clotting and for building healthy bones. The National Osteoporosis Foundation recommends a daily calcium intake of 1000-1200 mg/day for adult men and women. While calcium is contained in some foods, most adults do not get enough calcium in their diets and take supplements. Unfortunately some of the supplements have side effects such as gastric distress, making them difficult for some patients to take on a regular basis.
A study is designed to test whether there is a difference in mean daily calcium intake in adults with normal bone density, adults with osteopenia (a low bone density which may lead to osteoporosis) and adults with osteoporosis. Adults 60 years of age with normal bone density, osteopenia and osteoporosis are selected at random from hospital records and invited to participate in the study. Each participant's daily calcium intake is measured based on reported food intake and supplements. The data are shown below.
|
Normal Bone Density |
Osteopenia |
Osteoporosis |
|---|---|---|
|
1200 |
1000 |
890 |
|
1000 |
1100 |
650 |
|
980 |
700 |
1100 |
|
900 |
800 |
900 |
|
750 |
500 |
400 |
|
800 |
700 |
350 |
Is there a statistically significant difference in mean calcium intake in patients with normal bone density as compared to patients with osteopenia and osteoporosis? We will run the ANOVA using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance
H0: μ1 = μ2 = μ3 H1: Means are not all equal α=0.05
- Step 2. Select the appropriate test statistic.
The test statistic is the F statistic for ANOVA, F=MSB/MSE.
- Step 3. Set up decision rule.
In order to determine the critical value of F we need degrees of freedom, df1=k-1 and df2=N-k. In this example, df1=k-1=3-1=2 and df2=N-k=18-3=15. The critical value is 3.68 and the decision rule is as follows: Reject H0 if F > 3.68.
- Step 4. Compute the test statistic.
To organize our computations we will complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean.
|
Normal Bone Density |
Osteopenia |
Osteoporosis |
|---|---|---|
|
n1=6 |
n2=6 |
n3=6 |
|
|
|
|
If we pool all N=18 observations, the overall mean is 817.8.
We can now compute:

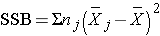
Substituting:

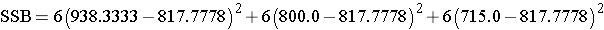
Finally,

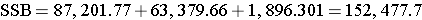
Next,

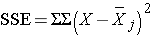
SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants with normal bone density:
|
Normal Bone Density |
(X - 938.3) |
(X - 938.3333)2 |
|---|---|---|
|
1200 |
261.6667 |
68,486.9 |
|
1000 |
61.6667 |
3,806.9 |
|
980 |
41.6667 |
1,738.9 |
|
900 |
-38.3333 |
1,466.9 |
|
750 |
-188.333 |
35,456.9 |
|
800 |
-138.333 |
19,126.9 |
|
Total |
0 |
130,083.3 |
Thus, 
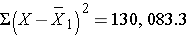
For participants with osteopenia:
|
Osteopenia |
(X - 800.0) |
(X - 800.0)2 |
|---|---|---|
|
1000 |
200 |
40,000 |
|
1100 |
300 |
90,000 |
|
700 |
-100 |
10,000 |
|
800 |
0 |
0 |
|
500 |
-300 |
90,000 |
|
700 |
-100 |
10,000 |
|
Total |
0 |
240,000 |
Thus, 
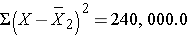
For participants with osteoporosis:
|
Osteoporosis |
(X - 715.0) |
(X - 715.0)2 |
|---|---|---|
|
890 |
175 |
30,625 |
|
650 |
-65 |
4,225 |
|
1100 |
385 |
148,225 |
|
900 |
185 |
34,225 |
|
400 |
-315 |
99,225 |
|
350 |
-365 |
133,225 |
|
Total |
0 |
449,750 |
Thus, 
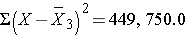

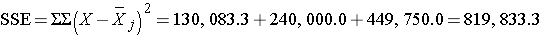
We can now construct the ANOVA table.
|
Source of Variation |
Sums of Squares (SS) |
Degrees of freedom (df) |
Mean Squares (MS) |
F |
|---|---|---|---|---|
|
Between Treatments |
152,477.7 |
2 |
76,238.6 |
1.395 |
|
Error or Residual |
819,833.3 |
15 |
54,655.5 |
|
|
Total |
972,311.0 |
17 |
- Step 5. Conclusion.
We do not reject H0 because 1.395 < 3.68. We do not have statistically significant evidence at a =0.05 to show that there is a difference in mean calcium intake in patients with normal bone density as compared to osteopenia and osterporosis. Are the differences in mean calcium intake clinically meaningful? If so, what might account for the lack of statistical significance?
One-Way ANOVA in R
The video below by Mike Marin demonstrates how to perform analysis of variance in R. It also covers some other statistical issues, but the initial part of the video will be useful to you.