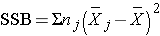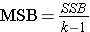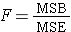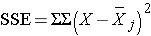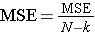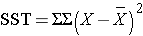The ANOVA Procedure

---

We will next illustrate the ANOVA procedure using the five step approach. Because the computation of the test statistic is involved, the computations are often organized in an ANOVA table. The ANOVA table breaks down the components of variation in the data into variation between treatments and error or residual variation. Statistical computing packages also produce ANOVA tables as part of their standard output for ANOVA, and the ANOVA table is set up as follows: 

Source of Variation	Sums of Squares (SS)	Degrees of Freedom (df)	Mean Squares (MS)	F
Between Treatments		k-1
Error (or Residual)		N-k
Total		N-1

 

where  

• X = individual observation,

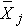• = sample mean of the j^th treatment (or group),
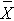• = overall sample mean,
• k = the number of treatments or independent comparison groups, and
• N = total number of observations or total sample size.

The ANOVA table above is organized as follows.

• The first column is entitled "Source of Variation" and delineates the between treatment and error or residual variation. The total variation is the sum of the between treatment and error variation.
• The second column is entitled "Sums of Squares (SS)". The between treatment sums of squares is

 

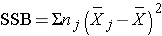
and is computed by summing the squared differences between each treatment (or group) mean and the overall mean. The squared differences are weighted by the sample sizes per group (n_j). The error sums of squares is:

 

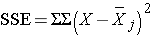
and is computed by summing the squared differences between each observation and its group mean (i.e., the squared differences between each observation in group 1 and the group 1 mean, the squared differences between each observation in group 2 and the group 2 mean, and so on). The double summation ( SS ) indicates summation of the squared differences within each treatment and then summation of these totals across treatments to produce a single value. (This will be illustrated in the following examples). The total sums of squares is:

 

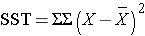
and is computed by summing the squared differences between each observation and the overall sample mean. In an ANOVA, data are organized by comparison or treatment groups. If all of the data were pooled into a single sample, SST would reflect the numerator of the sample variance computed on the pooled or total sample. SST does not figure into the F statistic directly. However, SST = SSB + SSE, thus if two sums of squares are known, the third can be computed from the other two.

• The third column contains degrees of freedom. The between treatment degrees of freedom is df₁ = k-1. The error degrees of freedom is df₂ = N - k. The total degrees of freedom is N-1 (and it is also true that (k-1) + (N-k) = N-1).

• The fourth column contains "Mean Squares (MS)" which are computed by dividing sums of squares (SS) by degrees of freedom (df), row by row. Specifically, MSB=SSB/(k-1) and MSE=SSE/(N-k). Dividing SST/(N-1) produces the variance of the total sample. The F statistic is in the rightmost column of the ANOVA table and is computed by taking the ratio of MSB/MSE.  

Example:

A clinical trial is run to compare weight loss programs and participants are randomly assigned to one of the comparison programs and are counseled on the details of the assigned program. Participants follow the assigned program for 8 weeks. The outcome of interest is weight loss, defined as the difference in weight measured at the start of the study (baseline) and weight measured at the end of the study (8 weeks), measured in pounds.  

Three popular weight loss programs are considered. The first is a low calorie diet. The second is a low fat diet and the third is a low carbohydrate diet. For comparison purposes, a fourth group is considered as a control group. Participants in the fourth group are told that they are participating in a study of healthy behaviors with weight loss only one component of interest. The control group is included here to assess the placebo effect (i.e., weight loss due to simply participating in the study). A total of twenty patients agree to participate in the study and are randomly assigned to one of the four diet groups. Weights are measured at baseline and patients are counseled on the proper implementation of the assigned diet (with the exception of the control group). After 8 weeks, each patient's weight is again measured and the difference in weights is computed by subtracting the 8 week weight from the baseline weight. Positive differences indicate weight losses and negative differences indicate weight gains. For interpretation purposes, we refer to the differences in weights as weight losses and the observed weight losses are shown below.

Low Calorie	Low Fat	Low Carbohydrate	Control
8	2	3	2
9	4	5	2
6	3	4	-1
7	5	2	0
3	1	3	3

Is there a statistically significant difference in the mean weight loss among the four diets?  We will run the ANOVA using the five-step approach.

 

• Step 1. Set up hypotheses and determine level of significance

H₀: μ₁ = μ₂ = μ₃ = μ₄ H₁: Means are not all equal              α=0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is the F statistic for ANOVA, F=MSB/MSE.

• Step 3. Set up decision rule.  

The appropriate critical value can be found in a table of probabilities for the F distribution(see "Other Resources"). In order to determine the critical value of F we need degrees of freedom, df₁=k-1 and df₂=N-k. In this example, df₁=k-1=4-1=3 and df₂=N-k=20-4=16. The critical value is 3.24 and the decision rule is as follows: Reject H₀ if F > 3.24.

• Step 4. Compute the test statistic.  

To organize our computations we complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean based on the total sample.  

	Low Calorie	Low Fat	Low Carbohydrate	Control
n	5	5	5	5
Group mean	6.6	3.0	3.4	1.2

If we pool all N=20 observations, the overall mean is 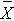= 3.6.

We can now compute

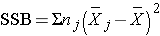
So, in this case:

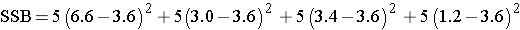
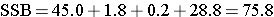
Next we compute,

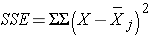
SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants in the low calorie diet:  

Low Calorie	(X - 6.6)	(X - 6.6)2
8	1.4	2.0
9	2.4	5.8
6	-0.6	0.4
7	0.4	0.2
3	-3.6	13.0
Totals	0	21.4

Thus,

 

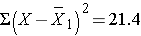
For the participants in the low fat diet:  

Low Fat	(X - 3.0)	(X - 3.0)2
2	-1.0	1.0
4	1.0	1.0
3	0.0	0.0
5	2.0	4.0
1	-2.0	4.0
Totals	0	10.0

 Thus,

 

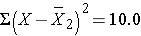
For the participants in the low carbohydrate diet:  

Low Carbohydrate	(X - 3.4)	(X - 3.4)2
3	-0.4	0.2
5	1.6	2.6
4	0.6	0.4
2	-1.4	2.0
3	-0.4	0.2
Totals	0	5.4

Thus,

 

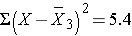
For the participants in the control group:

Control	(X - 1.2)	(X - 1.2)2
2	0.8	0.6
2	0.8	0.6
-1	-2.2	4.8
0	-1.2	1.4
3	1.8	3.2
Totals	0	10.6

Thus,

 

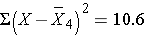
Therefore,  

 

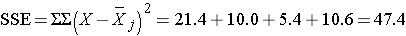
We can now construct the ANOVA table.

Source of Variation	Sums of Squares (SS)	Degrees of Freedom (df)	Means Squares (MS)	F
Between Treatmenst	75.8	4-1=3	75.8/3=25.3	25.3/3.0=8.43
Error (or Residual)	47.4	20-4=16	47.4/16=3.0
Total	123.2	20-1=19

 

• Step 5. Conclusion.  

We reject H₀ because 8.43 > 3.24. We have statistically significant evidence at α=0.05 to show that there is a difference in mean weight loss among the four diets.    

ANOVA is a test that provides a global assessment of a statistical difference in more than two independent means. In this example, we find that there is a statistically significant difference in mean weight loss among the four diets considered. In addition to reporting the results of the statistical test of hypothesis (i.e., that there is a statistically significant difference in mean weight losses at α=0.05), investigators should also report the observed sample means to facilitate interpretation of the results. In this example, participants in the low calorie diet lost an average of 6.6 pounds over 8 weeks, as compared to 3.0 and 3.4 pounds in the low fat and low carbohydrate groups, respectively. Participants in the control group lost an average of 1.2 pounds which could be called the placebo effect because these participants were not participating in an active arm of the trial specifically targeted for weight loss. Are the observed weight losses clinically meaningful?

return to top | previous page | next page