Confidence Intervals for Measures of Association
Measures of association are calculated by comparing two groups and computing a risk ratio, a risk difference (or rate ratios and rate differences), or, in the case of a case-control study, an odds ratio. These types of point estimates summarize the magnitude of association with a single number that captures the frequencies in both groups. These point estimates, of course, are also subject to random error, and one can indicate the degree of precision in these estimates by computing confidence intervals for them.
There are several methods for computing confidence intervals for estimated measures of association as well. You will not be responsible for these formulas; they are presented so you can see the components of the confidence interval.

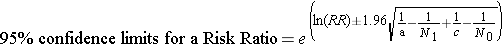
where "RR" is the risk ratio, "a" is the number of events in the exposed group, "N1" in the number of subjects in the exposed group, "c" is the number of events in the unexposed group, and N0 is the number of subjects in the unexposed group.


where IRR is the incidence rate ratio, "a" is the number of events in the exposed group, and"b" is the number of events in the unexposed group.

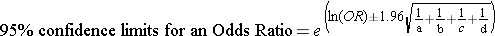
where "OR" is the odds ratio, "a" is the number of cases in the exposed group, "b" is the number of cases in the unexposed group, "c" is the number of controls in the exposed group, and "d" is the number of controls in the unexposed group.
Interpretation of the 95% Confidence Interval for an Odds Ratio or Risk Ratio
As noted previously, a 95% confidence interval means that if the same population were sampled on numerous occasions and confidence interval estimates were made on each occasion, the resulting intervals would contain the true population parameter in approximately 95% of the cases, assuming that there were no biases or confounding. However, people generally apply this probability to a single study. Consequently, an odds ratio of 5.2 with a confidence interval of 3.2 to 7.2 suggests that there is a 95% probability that the true odds ratio would be likely to lie in the range 3.2-7.2 assuming there is no bias or confounding. The interpretation of the 95% confidence interval for a risk ratio, a rate ratio, or a risk difference would be similar.