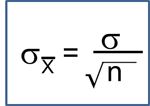Author:
Lisa Sullivan, PhD
Professor of Biostatistics
Boston University School of Public Health

Introduction
Probabilities are numbers that reflect the likelihood that a particular event will occur. We hear about probabilities in many every-day situations ranging from weather forecasts (probability of rain or snow) to the lottery (probability of hitting the big jackpot). In biostatistical applications, it is probability theory that underlies statistical inference. Statistical inference involves making generalizations or inferences about unknown population parameters. After selecting a sample from the population of interest, we measure the characteristic under study, summarize this characteristic in our sample and then make inferences about the population based on what we observe in the sample. In this module we will discuss methods of sampling, basic concepts of probability, and applications of probability theory. In subsequent modules we will discuss statistical inference in detail and present methods that will enable you to make inferences about a population based on a single sample.
After selecting a sample from the population of interest, we measure the characteristic under study, summarize this characteristic in our sample and then make inferences about the population based on what we observe in the sample. In this module we will discuss methods of sampling, basic concepts of probability, and applications of probability theory. In subsequent modules we will discuss statistical inference in detail and present methods that will enable you to make inferences about a population based on a single sample.
Learning Objectives
After completing this module, the student will be able to:
- Distinguish between methods of probability sampling and non-probability sampling
- Compute and interpret unconditional and conditional probabilities
- Evaluate and interpret independence of events
- Explain the key features of the binomial distribution model
- Calculate probabilities using the binomial formula
- Explain the key features of the normal distribution model
- Calculate probabilities using the standard normal distribution table
- Compute and interpret percentiles of the normal distribution
- Define and interpret the standard error
- Explain sampling variability
- Apply and interpret the results of the Central Limit Theorem