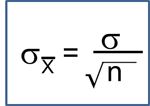Bayes's Theorem
Chris Wiggins, an associate professor of applied mathematics at Columbia University, posed the following question in an article in Scientific American: Link to the article in Scientific American:
"A patient goes to see a doctor. The doctor performs a test with 99 percent reliability--that is, 99 percent of people who are sick test positive and 99 percent of the healthy people test negative. The doctor knows that only 1 percent of the people in the country are sick. Now the question is: if the patient tests positive, what are the chances the patient is sick?"
The intuitive answer is 99 percent, but the correct answer is 50 percent...."
The solution to this question can easily be calculated using Bayes's theorem. Bayes, who was a reverend who lived from 1702 to 1761 stated that the probability you test positive AND are sick is the product of the likelihood that you test positive GIVEN that you are sick and the "prior" probability that you are sick (the prevalence in the population). Bayes's theorem allows one to compute a conditional probability based on the available information.
Bayes's Theorem

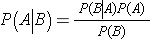
P(A) is the probability of event A
P(B) is the probability of event B
P(A|B) is the probability of observing event A if B is true
P(B|A) is the probability of observing event B if A is true.
Wiggins's explanation can be summarized with the help of the following table which illustrates the scenario in a hypothetical population of 10,000 people:
|
|
Diseased |
Not Diseased |
|
|---|---|---|---|
|
Test + |
99 |
99 |
198 |
|
Test - |
1 |
9,801 |
9,802 |
|
|
100 |
9,900 |
10,000 |
In this scenario P(A) is the unconditional probability of disease; here it is 100/10,000 = 0.01.
P(B) is the unconditional probability of a positive test; here it is 198/10,000 = 0.0198..
What we want to know is P (A | B), i.e., the probability of disease (A), given that the patient has a positive test (B). We know that prevalence of disease (the unconditional probability of disease) is 1% or 0.01; this is represented by P(A). Therefore, in a population of 10,000 there will be 100 diseased people and 9,900 non-diseased people. We also know the sensitivity of the test is 99%, i.e., P(B | A) = 0.99; therefore, among the 100 diseased people, 99 will test positive. We also know that the specificity is also 99%, or that there is a 1% error rate in non-diseased people. Therefore, among the 9,900 non-diseased people, 99 will have a positive test. And from these numbers, it follows that the unconditional probability of a positive test is 198/10,000 = 0.0198; this is P(B).
Thus, P(A | B) = (0.99 x 0.01) / 0.0198 = 0.50 = 50%.
From the table above, we can also see that given a positive test (subjects in the Test + row), the probability of disease is 99/198 = 0.05 = 50%.
Another Example:
Suppose a patient exhibits symptoms that make her physician concerned that she may have a particular disease. The disease is relatively rare in this population, with a prevalence of 0.2% (meaning it affects 2 out of every 1,000 persons). The physician recommends a screening test that costs $250 and requires a blood sample. Before agreeing to the screening test, the patient wants to know what will be learned from the test, specifically she wants to know the probability of disease, given a positive test result, i.e., P(Disease | Screen Positive).
The physician reports that the screening test is widely used and has a reported sensitivity of 85%. In addition, the test comes back positive 8% of the time and negative 92% of the time.
The information that is available is as follows:
- P(Disease)=0.002, i.e., prevalence = 0.002
- P(Screen Positive | Disease)=0.85, i.e., the probability of screening positive, given the presence of disease is 85% (the sensitivity of the test), and
- P(Screen Positive)=0.08, i.e., the probability of screening positive overall is 8% or 0.08. We can now substitute the values into the above equation to compute the desired probability,
Based on the available information, we could piece this together using a hypothetical population of 100,000 people. Given the available information this test would produce the results summarized in the table below. Point your mouse at the numbers in the table in order to get an explanation of how they were calculated.
|
|
Diseased |
Not Diseased |
|
|---|---|---|---|
|
Test + |
|||
|
Test - |
|||
|
|
100,000 |
The answer to the patient's question also could be computed from Bayes's Theorem:

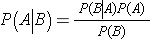
We know that P(Disease)=0.002, P(Screen Positive | Disease)=0.85 and P(Screen Positive)=0.08. We can now substitute the values into the above equation to compute the desired probability,
P(Disease | Screen Positive) = (0.85)(0.002)/(0.08) = 0.021.
If the patient undergoes the test and it comes back positive, there is a 2.1% chance that he has the disease. Also, note, however, that without the test, there is a 0.2% chance that he has the disease (the prevalence in the population). In view of this, do you think the patient have the screening test?
Another important question that the patient might ask is, what is the chance of a false positive result? Specifically, what is P(Screen Positive| No Disease)? We can compute this conditional probability with the available information using Bayes Theorem.

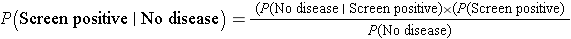
By substituting the probabilities in this scenario, we get:


Thus, using Bayes Theorem, there is a 7.8% probability that the screening test will be positive in patients free of disease, which is the false positive fraction of the test.
Complementary Events
Note that if P(Disease) = 0.002, then P(No Disease)=1-0.002. The events, Disease and No Disease, are called complementary events. The "No Disease" group includes all members of the population not in the "Disease" group. The sum of the probabilities of complementary events must equal 1 (i.e., P(Disease) + P(No Disease) = 1). Similarly, P(No Disease | Screen Positive) + P(Disease | Screen Positive) = 1.
Probability Models
To compute the probabilities in the previous section, we counted the number of participants that had a particular outcome or characteristic of interest, and divided by the population size. For conditional probabilities, the population size (denominator) was modified to reflect the sub-population of interest.
In each of the examples in the previous sections, we had a tabulation of the population (the sampling frame) that allowed us to compute the desired probabilities. However, there are instances in which a complete tabulation is not available. In some of these instances, probability models or mathematical equations can be used to generate probabilities. There are many probability models, and the model appropriate for a specific application depends on the specific attributes of the application. There are two particularly useful probability models:
- the binomial distribution model, which is useful for computing probabilities about a discrete variable
- the normal distribution model, which is useful for computing probabilities about a continuous variable.
These probability models are extremely important in statistical inference, and we will discuss these next.