Comparing the Means in Two Independent Samples (Unpaired t-test)
Suppose investigators want to assess the effectiveness of a new drug in lowering cholesterol, and they want to conduct a small clinical trial in which patients were randomized to receive the new drug or placebo, and total cholesterol was measured after six weeks on the assigned treatment. The table below shows the results.
| Sample Size (n) | Mean Cholesterol (6 wk) | SD | |
| New drug | 15 | 195.9 | 28.7 |
| Placebo | 15 | 217.4 | 30.3 |
Is there sufficiently strong evidence of a difference in mean cholesterol for patients on the new drug compared to patients receiving the placebo?
Note that SD is used to characterize individual variability within each group, although we will use SE when conducting a hypothesis test to compare the means.
H0: μ1 = μ2
H1:μ1≠ μ2
Since we are comparing the means in two independent groups (i.e., different patients in the two treatment groups), we will use the two independent sample t-test (aka, unpaired t-test) shown below. "Sp" is the pooled standard deviation for the two groups.

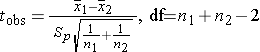
where

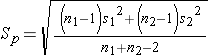
Equal Variance Assumption
Use of this test assumes that the variance for the two groups are more or less equal. Recall that variance = the square of the standard deviation, and note that s12 and s22 are the variances for the two samples, and they are included in the calculation of Sp. We can test the assumption of equal variance by computing the ratio of the two variances, and if the ratio is in the range of 0.5 to 2.0, then the assumption is adequately met. If this is not the case, a different equation must be used (the Welch t-test), but if we are using R, there is a simple way to make this adjustment, as you will see.
In the example we are currently using the ratio of the variances is
Ratio = 28.72 / 30.32 = 0.90
so the assumption is met.
Next, we need to compute the pooled standard deviation.

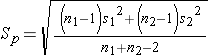

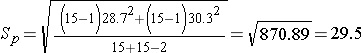
So, Sp=29.5 will be plugged into the equation for the test statistic as shown in the next step.

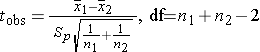

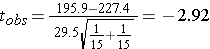
df = n1 + n2 - 2 = 28
We can use R to compute the two-tailed p-value:
2*pt(-2.92,28)
[1] 0.006840069
The p-value is 0.007, so there is sufficient evidence to reject the null hypothesis.
Conclusion:
Mean cholesterol is statistically significantly lower in patients on treatment as compared to placebo: 195.9 ± SD: 28.7 vs. 217.4 ± SD: 30.3, p=0.007).