Page:
1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10

Standardized Incidence Ratios (SIR)

A standardized incidence ratio, or SIR, is the ratio of the number of cancers observed in a community compared to what would be expected if the community's rate was the same as the state average.

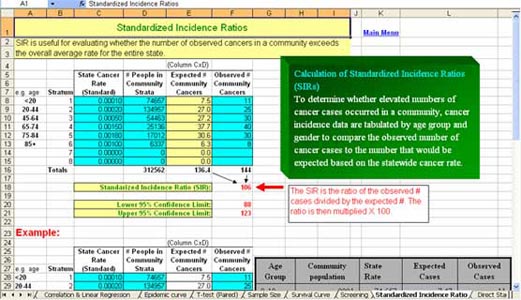
The rate of cancer is likely to vary by age, and specific communities may have age distributions that differ from that of the state overall. However, one can take this into account by using the states age-specific rates to calculate the number of cancers expected in each age bracket in the community and then adding these up. Consider the example illustrated in the table below, which considers date for a particular type of cancer, such as leukemia. Column B shows the number of residents in each of the age groups specified in column A. Column C shows the overall state average rate of leukemia for each age group. The town has 74,657 resident in the 0-19 year old age group. If they had the same frequency of leukemia as the state average (0.0001), then we would expect the town to have 74,657 x 0.0001 = 7.47 leukemias in the specified time period. The expected number of cases are listed in column D, and they are calculated for each age group by multiplying columns B & C. The last column lists the number of cases that were actually reported to the cancer registry in the specified time period. Once the table has been completed in this fashon, one can add up the number of expected cases for all age groups; in this case the sum for column D is 136.35. One can similarly compute the total number of cases observed in column E; in this case the sum is 144.

A) Age Group	B) Town Population	C) State Rate	D) Expected Cases (BxC)	E) Observed Cases
0-19	74,657	0.0001	7.47	11
20-44	134,957	0.0002	26.99	25
45-64	54,463	0.0005	27.23	30
65-74	25,136	0.0015	37.70	40
75-84	17,012	0.0018	30.62	30
85+	6,337	0.0010	6.34	8

After computing the total number of observed leukemias and the total number of leukemias that would have been expected if the town had the same age-specific rates as the state average, one can then express this as the ratio of observed/expected cases. In this example the SIR would be 106.

SIR = (O/E) x 100 = (144/136.35) x 100 = 106

An SIR = 106 suggests that the town's rate of leukemia was only 6% greater than expected based on the overal state average for that type of cancer.

Is the Incidence in Our Community Really Greater?
If the community's cancer incidence were perfectly in line with the state average, the SIR would equal 100; this is the null value, meaning that there is no difference. In the previous example the SIR of 106 suggests that the rate of cancer in the community is 6% higher than the state average, but we might ask whether this increase is simply due to random variation in cancer occurrence. For example, suppose the expected number of mesotheliomas (a cancer of the lining of the lung) is 3 for a given community, but they observe 5 in a given year. SIR = (5/3) x 100 = 167 We could interpret this as a 67% greater incidence, but it is only due to two more cases, so the increase could be simply the result of random variation in cancer occurrence rather than to a significant difference in this community. In contrast, suppose the expected number of breast cancers for a community was 30, but they observed 50 cases during the year. This is also a 67% increase, but it represents 20 cases more than expected, and therefore raises our concern that the increase may not be simply the result of random variation.

Is the Incidence in Our Community Really Greater?

If the community's cancer incidence were perfectly in line with the state average, the SIR would equal 100; this is the null value, meaning that there is no difference.

In the previous example the SIR of 106 suggests that the rate of cancer in the community is 6% higher than the state average, but we might ask whether this increase is simply due to random variation in cancer occurrence.

For example, suppose the expected number of mesotheliomas (a cancer of the lining of the lung) is 3 for a given community, but they observe 5 in a given year.

SIR = (5/3) x 100 = 167

We could interpret this as a 67% greater incidence, but it is only due to two more cases, so the increase could be simply the result of random variation in cancer occurrence rather than to a significant difference in this community.

In contrast, suppose the expected number of breast cancers for a community was 30, but they observed 50 cases during the year. This is also a 67% increase, but it represents 20 cases more than expected, and therefore raises our concern that the increase may not be simply the result of random variation.

The next section addresses how confidence intervals can be used to interpret these findings.

The 95% Confidence Interval for the SIR

Interpretation of an elevated SIR is facilitated by calculating a 95% confidence interval.The SIR represents an estimate of how much the community's cancer incidence differs from the average for the state. The 95% confidence interval for an SIR is the range within which the true SIR lies, with 95% confidence, taking into account the actual numbers that were expected and observed. If 3 mesotheliomas were expected in a community, but 5 were observed, the confidence interval would be 0-333. This very wide confidence interval means that based on these data, the true incidence ratio is somewhere between 0 and 333, with 95% confidence. This extraordinarily wide interval reflects the imprecision of our estimate and our lack of confidence in its accuracy.

In contrast, if 30 breast cancers were expected, but 50 were observed, the confidence interval would range from 120-213. Thus, the community has at least a 20% greater incidence, with 95% confidence, although the increase could be substantially higher. Note that this confidence interval does not include the null value (100). Therefore, we can interpret this as a statistically significant difference, meaning that there is less than a 5% probability that the difference observed is simply the result of random variation in cancer occurrence.

The calculation of SIR and the 95% confidence interval is automatically done for you in one of the worksheets in the Excel file "Epi_Tools.XLS," which can be downloaded from "Other Resources" to the right. This file contains a number of worksheets that perform an array of statistical calculations very simply.

Follow the link to "Epi_Tools.XLS". (Save the file on your computer.) From the main menu, click the link for "Standardized Incidence Ratio."

Mesothelioma is an uncommon type of lung cancer that is associated with exposure to asbestos and smoking. The table below summarizes actual data on the incidence of mesothelioma in Massachusetts from 1985-2000. Use these data to compute the SIR for Weymouth during this time period. Compute the SIR by hand, and then check your answer by entering these data into the worksheet for computing SIRs in the Epi_Tools.XLS spreadsheet that can be downloaded from "Other Resources" on the right. The worksheet will also compute the 95% confidence interval for the SIR. Use these computations to answer the quiz questions beneath the table.

Age	MA Population 1985-2000	MA Cases	MA Rate	Weymouth Population 1985-2000	Weymouth Observed Cases
45-64	1,230,620	455	0.00037	11,612	16
65-74	438,407	640	0.00146	4,242	17
75-84	276,570	522	0.00189	2,460	14
85+	99,333	117	0.00118	800	3

Value: 1

return to top | previous page | next page