Mann Whitney U Test (Wilcoxon Rank Sum Test)
The modules on hypothesis testing presented techniques for testing the equality of means in two independent samples. An underlying assumption for appropriate use of the tests described was that the continuous outcome was approximately normally distributed or that the samples were sufficiently large (usually n1> 30 and n2> 30) to justify their use based on the Central Limit Theorem. When comparing two independent samples when the outcome is not normally distributed and the samples are small, a nonparametric test is appropriate.
A popular nonparametric test to compare outcomes between two independent groups is the Mann Whitney U test. The Mann Whitney U test, sometimes called the Mann Whitney Wilcoxon Test or the Wilcoxon Rank Sum Test, is used to test whether two samples are likely to derive from the same population (i.e., that the two populations have the same shape). Some investigators interpret this test as comparing the medians between the two populations. Recall that the parametric test compares the means (H0: μ1=μ2) between independent groups.
In contrast, the null and two-sided research hypotheses for the nonparametric test are stated as follows:
H0: The two populations are equal versus
H1: The two populations are not equal.
This test is often performed as a two-sided test and, thus, the research hypothesis indicates that the populations are not equal as opposed to specifying directionality. A one-sided research hypothesis is used if interest lies in detecting a positive or negative shift in one population as compared to the other. The procedure for the test involves pooling the observations from the two samples into one combined sample, keeping track of which sample each observation comes from, and then ranking lowest to highest from 1 to n1+n2, respectively.
Example:
Consider a Phase II clinical trial designed to investigate the effectiveness of a new drug to reduce symptoms of asthma in children. A total of n=10 participants are randomized to receive either the new drug or a placebo. Participants are asked to record the number of episodes of shortness of breath over a 1 week period following receipt of the assigned treatment. The data are shown below.
|
Placebo |
7 |
5 |
6 |
4 |
12 |
|
New Drug |
3 |
6 |
4 |
2 |
1 |
Is there a difference in the number of episodes of shortness of breath over a 1 week period in participants receiving the new drug as compared to those receiving the placebo? By inspection, it appears that participants receiving the placebo have more episodes of shortness of breath, but is this statistically significant?
In this example, the outcome is a count and in this sample the data do not follow a normal distribution.
Frequency Histogram of Number of Episodes of Shortness of Breath
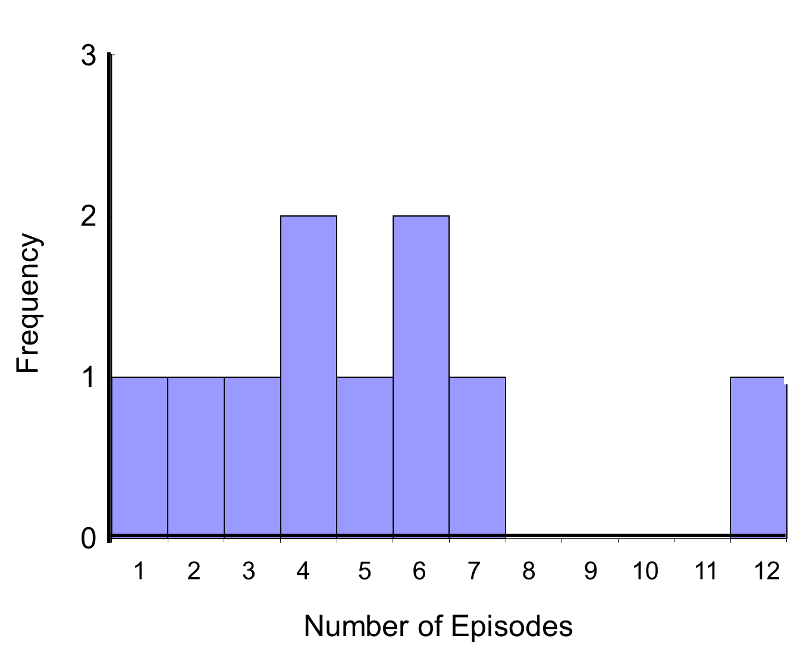
In addition, the sample size is small (n1=n2=5), so a nonparametric test is appropriate. The hypothesis is given below, and we run the test at the 5% level of significance (i.e., α=0.05).
H0: The two populations are equal versus
H1: The two populations are not equal.
Note that if the null hypothesis is true (i.e., the two populations are equal), we expect to see similar numbers of episodes of shortness of breath in each of the two treatment groups, and we would expect to see some participants reporting few episodes and some reporting more episodes in each group. This does not appear to be the case with the observed data. A test of hypothesis is needed to determine whether the observed data is evidence of a statistically significant difference in populations.
The first step is to assign ranks and to do so we order the data from smallest to largest. This is done on the combined or total sample (i.e., pooling the data from the two treatment groups (n=10)), and assigning ranks from 1 to 10, as follows. We also need to keep track of the group assignments in the total sample.
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||
|---|---|---|---|---|---|
|
Placebo |
New Drug |
Placebo |
New Drug |
Placebo |
New Drug |
|
7 |
3 |
|
1 |
|
1 |
|
5 |
6 |
|
2 |
|
2 |
|
6 |
4 |
|
3 |
|
3 |
|
4 |
2 |
4 |
4 |
4.5 |
4.5 |
|
12 |
1 |
5 |
|
6 |
|
|
|
|
6 |
6 |
7.5 |
7.5 |
|
|
|
7 |
|
9 |
|
|
|
|
12 |
|
10 |
|
Note that the lower ranks (e.g., 1, 2 and 3) are assigned to responses in the new drug group while the higher ranks (e.g., 9, 10) are assigned to responses in the placebo group. Again, the goal of the test is to determine whether the observed data support a difference in the populations of responses. Recall that in parametric tests (discussed in the modules on hypothesis testing), when comparing means between two groups, we analyzed the difference in the sample means relative to their variability and summarized the sample information in a test statistic. A similar approach is employed here. Specifically, we produce a test statistic based on the ranks.
First, we sum the ranks in each group. In the placebo group, the sum of the ranks is 37; in the new drug group, the sum of the ranks is 18. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 10(11)/2=55 which is equal to 37+18 = 55.
For the test, we call the placebo group 1 and the new drug group 2 (assignment of groups 1 and 2 is arbitrary). We let R1 denote the sum of the ranks in group 1 (i.e., R1=37), and R2 denote the sum of the ranks in group 2 (i.e., R2=18). If the null hypothesis is true (i.e., if the two populations are equal), we expect R1 and R2 to be similar. In this example, the lower values (lower ranks) are clustered in the new drug group (group 2), while the higher values (higher ranks) are clustered in the placebo group (group 1). This is suggestive, but is the observed difference in the sums of the ranks simply due to chance? To answer this we will compute a test statistic to summarize the sample information and look up the corresponding value in a probability distribution.
Test Statistic for the Mann Whitney U Test
The test statistic for the Mann Whitney U Test is denoted U and is the smaller of U1 and U2, defined below.

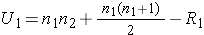

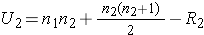
where R1 = sum of the ranks for group 1 and R2 = sum of the ranks for group 2.
For this example,

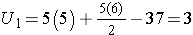

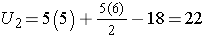
In our example, U=3. Is this evidence in support of the null or research hypothesis? Before we address this question, we consider the range of the test statistic U in two different situations.
Situation #1
Consider the situation where there is complete separation of the groups, supporting the research hypothesis that the two populations are not equal. If all of the higher numbers of episodes of shortness of breath (and thus all of the higher ranks) are in the placebo group, and all of the lower numbers of episodes (and ranks) are in the new drug group and that there are no ties, then:

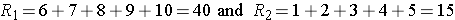
and

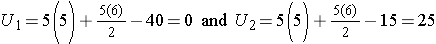
Therefore, when there is clearly a difference in the populations, U=0.
Situation #2
Consider a second situation where low and high scores are approximately evenly distributed in the two groups, supporting the null hypothesis that the groups are equal. If ranks of 2, 4, 6, 8 and 10 are assigned to the numbers of episodes of shortness of breath reported in the placebo group and ranks of 1, 3, 5, 7 and 9 are assigned to the numbers of episodes of shortness of breath reported in the new drug group, then:

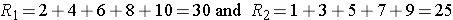 R1= 2+4+6+8+10 = 30 and R2= 1+3+5+7+9 = 25,
R1= 2+4+6+8+10 = 30 and R2= 1+3+5+7+9 = 25,
and

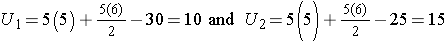
When there is clearly no difference between populations, then U=10.
Thus, smaller values of U support the research hypothesis, and larger values of U support the null hypothesis.
|
Key Concept: For any Mann-Whitney U test, the theoretical range of U is from 0 (complete separation between groups, H0 most likely false and H1 most likely true) to n1*n2 (little evidence in support of H1).
In every test, U1+U2 is always equal to n1*n2. In the example above, U can range from 0 to 25 and smaller values of U support the research hypothesis (i.e., we reject H0 if U is small). The procedure for determining exactly when to reject H0 is described below. |
In every test, we must determine whether the observed U supports the null or research hypothesis. This is done following the same approach used in parametric testing. Specifically, we determine a critical value of U such that if the observed value of U is less than or equal to the critical value, we reject H0 in favor of H1 and if the observed value of U exceeds the critical value we do not reject H0.
The critical value of U can be found in the table below. To determine the appropriate critical value we need sample sizes (for Example: n1=n2=5) and our two-sided level of significance (α=0.05). For Example 1 the critical value is 2, and the decision rule is to reject H0 if U < 2. We do not reject H0 because 3 > 2. We do not have statistically significant evidence at α =0.05, to show that the two populations of numbers of episodes of shortness of breath are not equal. However, in this example, the failure to reach statistical significance may be due to low power. The sample data suggest a difference, but the sample sizes are too small to conclude that there is a statistically significant difference.
Table of Critical Values for U
Example:
A new approach to prenatal care is proposed for pregnant women living in a rural community. The new program involves in-home visits during the course of pregnancy in addition to the usual or regularly scheduled visits. A pilot randomized trial with 15 pregnant women is designed to evaluate whether women who participate in the program deliver healthier babies than women receiving usual care. The outcome is the APGAR score measured 5 minutes after birth. Recall that APGAR scores range from 0 to 10 with scores of 7 or higher considered normal (healthy), 4-6 low and 0-3 critically low. The data are shown below.
measured 5 minutes after birth. Recall that APGAR scores range from 0 to 10 with scores of 7 or higher considered normal (healthy), 4-6 low and 0-3 critically low. The data are shown below.
|
Usual Care |
8 |
7 |
6 |
2 |
5 |
8 |
7 |
3 |
|
New Program |
9 |
9 |
7 |
8 |
10 |
9 |
6 |
|
Is there statistical evidence of a difference in APGAR scores in women receiving the new and enhanced versus usual prenatal care? We run the test using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance.
H0: The two populations are equal versus
H1: The two populations are not equal. α =0.05
- Step 2. Select the appropriate test statistic.
Because APGAR scores are not normally distributed and the samples are small (n1=8 and n2=7), we use the Mann Whitney U test. The test statistic is U, the smaller of

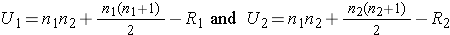
where R1 and R2 are the sums of the ranks in groups 1 and 2, respectively.
- Step 3. Set up decision rule.
The appropriate critical value can be found in the table above. To determine the appropriate critical value we need sample sizes (n1=8 and n2=7) and our two-sided level of significance (α=0.05). The critical value for this test with n1=8, n2=7 and α =0.05 is 10 and the decision rule is as follows: Reject H0 if U < 10.
- Step 4. Compute the test statistic.
The first step is to assign ranks of 1 through 15 to the smallest through largest values in the total sample, as follows:
|
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||
|---|---|---|---|---|---|
|
Usual Care |
New Program |
Usual Care |
New Program |
Usual Care |
New Program |
|
8 |
9 |
2 |
|
1 |
|
|
7 |
8 |
3 |
|
2 |
|
|
6 |
7 |
5 |
|
3 |
|
|
2 |
8 |
6 |
6 |
4.5 |
4.5 |
|
5 |
10 |
7 |
7 |
7 |
7 |
|
8 |
9 |
7 |
|
7 |
|
|
7 |
6 |
8 |
8 |
10.5 |
10.5 |
|
3 |
|
8 |
8 |
10.5 |
10.5 |
|
|
|
|
9 |
|
13.5 |
|
|
|
|
9 |
|
13.5 |
|
|
|
|
10 |
|
15 |
|
|
|
|
|
R1=45.5 |
R2=74.5 |
Next, we sum the ranks in each group. In the usual care group, the sum of the ranks is R1=45.5 and in the new program group, the sum of the ranks is R2=74.5. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 15(16)/2=120 which is equal to 45.5+74.5 = 120.
We now compute U1 and U2, as follows:

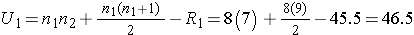

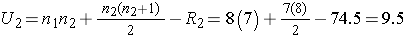
Thus, the test statistic is U=9.5.
- Step 5. Conclusion:
We reject H0 because 9.5 < 10. We have statistically significant evidence at α =0.05 to show that the populations of APGAR scores are not equal in women receiving usual prenatal care as compared to the new program of prenatal care.
Example:
A clinical trial is run to assess the effectiveness of a new anti-retroviral therapy for patients with HIV. Patients are randomized to receive a standard anti-retroviral therapy (usual care) or the new anti-retroviral therapy and are monitored for 3 months. The primary outcome is viral load which represents the number of HIV copies per milliliter of blood. A total of 30 participants are randomized and the data are shown below.
|
Standard Therapy |
7500 |
8000 |
2000 |
550 |
1250 |
1000 |
2250 |
6800 |
3400 |
6300 |
9100 |
970 |
1040 |
670 |
400 |
|
New Therapy |
400 |
250 |
800 |
1400 |
8000 |
7400 |
1020 |
6000 |
920 |
1420 |
2700 |
4200 |
5200 |
4100 |
undetectable |
Is there statistical evidence of a difference in viral load in patients receiving the standard versus the new anti-retroviral therapy?
- Step 1. Set up hypotheses and determine level of significance.
H0: The two populations are equal versus
H1: The two populations are not equal. α=0.05
- Step 2. Select the appropriate test statistic.
Because viral load measures are not normally distributed (with outliers as well as limits of detection (e.g., "undetectable")), we use the Mann-Whitney U test. The test statistic is U, the smaller of

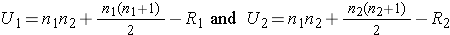
where R1 and R2 are the sums of the ranks in groups 1 and 2, respectively.
- Step 3. Set up the decision rule.
The critical value can be found in the table of critical values based on sample sizes (n1=n2=15) and a two-sided level of significance (α=0.05). The critical value 64 and the decision rule is as follows: Reject H0 if U < 64.
- Step 4. Compute the test statistic.
The first step is to assign ranks of 1 through 30 to the smallest through largest values in the total sample. Note in the table below, that the "undetectable" measurement is listed first in the ordered values (smallest) and assigned a rank of 1.
|
|
|
Total Sample (Ordered Smallest to Largest) |
Ranks |
||
|---|---|---|---|---|---|
|
Standard Anti-retroviral |
New Anti-retroviral |
Standard Anti-retroviral |
New Anti-retroviral |
Standard Anti-retroviral |
New Anti-retroviral |
|
7500 |
400 |
|
undetectable |
|
1 |
|
8000 |
250 |
|
250 |
|
2 |
|
2000 |
800 |
400 |
400 |
3.5 |
3.5 |
|
550 |
1400 |
550 |
|
5 |
|
|
1250 |
8000 |
670 |
|
6 |
|
|
1000 |
7400 |
|
800 |
|
7 |
|
2250 |
1020 |
|
920 |
|
8 |
|
6800 |
6000 |
970 |
|
9 |
|
|
3400 |
920 |
1000 |
|
10 |
|
|
6300 |
1420 |
|
1020 |
|
11 |
|
9100 |
2700 |
1040 |
|
12 |
|
|
970 |
4200 |
1250 |
|
13 |
|
|
1040 |
5200 |
|
1400 |
|
14 |
|
670 |
4100 |
|
1420 |
|
15 |
|
400 |
undetectable |
2000 |
|
16 |
|
|
|
|
2250 |
|
17 |
|
|
|
|
|
2700 |
|
18 |
|
|
|
3400 |
|
19 |
|
|
|
|
|
4100 |
|
20 |
|
|
|
|
4200 |
|
21 |
|
|
|
|
5200 |
|
22 |
|
|
|
|
6000 |
|
23 |
|
|
|
6300 |
|
24 |
|
|
|
|
6800 |
|
25 |
|
|
|
|
|
7400 |
|
26 |
|
|
|
7500 |
|
27 |
|
|
|
|
8000 |
8000 |
28.5 |
28.5 |
|
|
|
9100 |
|
30 |
|
|
|
|
|
|
R1 = 245 |
R2 = 220 |
Next, we sum the ranks in each group. In the standard anti-retroviral therapy group, the sum of the ranks is R1=245; in the new anti-retroviral therapy group, the sum of the ranks is R2=220. Recall that the sum of the ranks will always equal n(n+1)/2. As a check on our assignment of ranks, we have n(n+1)/2 = 30(31)/2=465 which is equal to 245+220 = 465. We now compute U1 and U2, as follows,

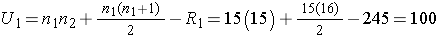

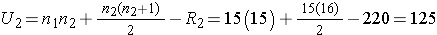
Thus, the test statistic is U=100.
- Step 5. Conclusion.
We do not reject H0 because 100 > 64. We do not have sufficient evidence to conclude that the treatment groups differ in viral load.