T-test for Two Dependent Samples (Paired or Matched Design)
The third application of a t-test that we will consider is for two dependent (paired or matched) samples. This can be applied in either of two types of comparisons.
- Pre-post Comparisons: One sample of subjects is measure twice under two different conditions, e.g., before and after receiving a drug.
- Comparison of Matched Samples: Two samples of pair-matched subjects, e.g., siblings or twins, or subjects matched by age and hospital ward
Example 1: Does an intervention increase knowledge about HIV transmission?
Early in the HIV epidemic, there was poor knowledge of HIV transmission risks among health care staff. A short training was developed to improve knowledge and attitudes around HIV disease. Was the training effective in improving knowledge?
Table - Mean ( ± SD) knowledge scores, pre- and post-intervention, n=15
| Pre-Intervention | Post-Intervention | Change |
| 18.3 ± 3.8 | 21.9 ± 4.4 | 3.53 ± 3.93 |
The raw data for this comparison is shown in the next table.
|
Subject |
Kscore1 | Kscore2 | difference |
|
1 |
17 | 22 | 5 |
|
2 |
17 | 21 | 4 |
|
3 |
15 | 21 | 6 |
|
4 |
19 | 26 | 7 |
|
5 |
18 | 20 | 2 |
|
6 |
14 | 14 | 0 |
|
7 |
27 | 31 | 4 |
|
8 |
20 | 18 | -2 |
|
9 |
12 | 22 | 10 |
|
10 |
21 | 20 | -1 |
|
11 |
20 | 27 | 7 |
|
12 |
24 | 23 | -1 |
|
13 |
17 | 15 | -2 |
|
14 |
17 | 24 | 7 |
|
15 |
17 | 24 | 7 |
| mean difference = | 3.533333 | ||
| sddiff= | 3.925497 | ||
| p-value= |
0.003634 |
The strategy is to calculate the pre-/post- difference in knowledge score for each person and determine whether the mean difference=0.
First, establish the null and alternative hypotheses.
- H0: μd = 0
- H1: μd ≠ 0
Then compute the test statistic for paired or matched samples

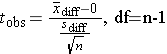

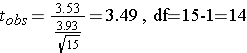
T-test of Two Dependent (paired) Samples Using R
For the example above we can compute the p-value using R. First, we compute the means.
> mean(Kscore1)
[1] 18.33333
> mean(Kscore2)
[1] 21.86667
Then we perform the t-test for two dependent samples.
> t.test(Kscore2,Kscore1,paired=TRUE)
Paired t-test
data: Kscore2 and Kscore1 t = 3.4861, df = 14, p-value = 0.003634
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.359466 5.707201
sample estimates:
mean of the differences
3.533333
The null hypothesis is that the mean change in knowledge scores from before to after is 0. However, the analyis shows that the mean difference is 3.53 with a 95% confidence interval that ranges from 1.36 to 5.7. Since the confidence interval does not include the null value of 0, the p-value must be < 0.05, and in fact it is 0.003634.