Hypothesis Testing
- A hypothesis is a testable statement that tries to explain relationships, and it can be accepted or rejected through scientific research.
- A fundamental hypothesis expresses one's belief or suspicion about a relationship, e.g., "Smoking causes lung cancer." This statement is not easily testable, however.
- A research hypothesis is a more precise and testable statement, such as, "People who smoke cigarettes regularly will have a higher incidence of lung cancer over a 10-year period than people who do not smoke cigarettes."
- The null hypothesis is that the groups do not differ. If there is sufficient evidence that this is not the case, then we reject the null hypothesis and accept the alternate: the groups are probably different.
Our general strategy is to specify a null and alternative hypothesis and then select and calculate the appropriate test statistic, which we will use to determine the p-value, i.e., the probability of finding differences this great or greater due to sampling error (chance). If the p-value is very small, it indicates a low probability of observing these difference as a result of sampling error, i.e., the null hypothesis is probably not true, so we will reject the null hypothesis and accept the alternative.
For continuous outcomes, there are three fundamental comparisons to make:
- One sample t-test: one sample is compared to an historical or external mean (μ0) ["s" is the standard deviation in the sample]

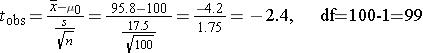
- Two independent sample t-test (unpaired t-test): the means of two independent (different) groups are compared. (Are the means in two groups the same?)

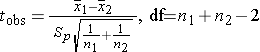
where

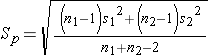
- Two dependent sample t-test (paired t-test): two sets of matched or paired sets of data are compared

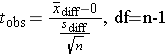
(There is also a procedure called analysis of variance (ANOVA) for comparing the means among more than two groups, but we will not address ANOVA in this course.)
Notice that all three of these tests generate a test statistic that takes into account:
- The magnitude of difference between the groups being compared, i.e., the "measure of effect," i.e., the numerator of the test statistic)
- The sample size and variability in the samples (the denominator in the test statistic)