Extensions
There are a number of important extensions of the approach that are beyond the scope of this text.
Time-Dependent Covariates
In the previous examples, we considered the effect of risk factors measured at the beginning of the study period, or at baseline, but there are many applications where the risk factors or predictors change over time. Suppose we wish to assess the impact of exposure to nicotine and alcohol during pregnancy on time to preterm delivery. Smoking and alcohol consumption may change during the course of pregnancy. These predictors are called time-dependent covariates and they can be incorporated into survival analysis models. The Cox proportional hazards regression model with time dependent covariates takes the form:

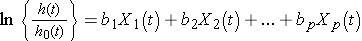
Notice that each of the predictors, X1, X2, ... , Xp, now has a time component. There are also many predictors, such as sex and race, that are independent of time. Survival analysis models can include both time dependent and time independent predictors simultaneously. Many statistical computing packages (e.g., SAS12) offer options for the inclusion of time dependent covariates. A difficult aspect of the analysis of time-dependent covariates is the appropriate measurement and management of these data for inclusion in the models.
Proportionality Assumption
A very important assumption for the appropriate use of the log rank test and the Cox proportional hazards regression model is the proportionality assumption.
Specifically, we assume that the hazards are proportional over time which implies that the effect of a risk factor is constant over time. There are several approaches to assess the proportionality assumption, some are based on statistical tests and others involve graphical assessments.
In the statistical testing approach, predictor by time interaction effects are included in the model and tested for statistical significance. If one (or more) of the predictor by time interactions reaches statistical significance (e.g., p<0.05), then the assumption of proportionality is violated. An alternative approach to assessing proportionality is through graphical analysis. There are several graphical displays that can be used to assess whether the proportional hazards assumption is reasonable. These are often based on residuals and examine trends (or lack thereof) over time. More details can be found in Hosmer and Lemeshow1.
If either a statistical test or a graphical analysis suggest that the hazards are not proportional over time, then the Cox proportional hazards model is not appropriate, and adjustments must be made to account for non-proportionality. One approach is to stratify the data into groups such that within groups the hazards are proportional, and different baseline hazards are estimated in each stratum (as opposed to a single baseline hazard as was the case for the model presented earlier). Many statistical computing packages offer this option.
Competing Risks
The competing risks issue is one in which there are several possible outcome events of interest. For example, a prospective study may be conducted to assess risk factors for time to incident cardiovascular disease. Cardiovascular disease includes myocardial infarction, coronary heart disease, coronary insufficiency and many other conditions. The investigator measures whether each of the component outcomes occurs during the study observation period as well as the time to each distinct event. The goal of the analysis is to determine the risk factors for each specific outcome and the outcomes are correlated. Interested readers should see Kalbfleisch and Prentice10 for more details.