Confidence Interval for Two Independent Samples, Dichotomous Outcome
It is common to compare two independent groups with respect to the presence or absence of a dichotomous characteristic or attribute, (e.g., prevalent cardiovascular disease or diabetes, current smoking status, cancer remission, or successful device implant). When the outcome is dichotomous, the analysis involves comparing the proportions of successes between the two groups. There are several ways of comparing proportions in two independent groups.
- One can compute a risk difference, which is computed by taking the difference in proportions between comparison groups and is similar to the estimate of the difference in means for a continuous outcome.
- The risk ratio (or relative risk) is another useful measure to compare proportions between two independent populations and it is computed by taking the ratio of proportions.
Generally the reference group (e.g., unexposed persons, persons without a risk factor or persons assigned to the control group in a clinical trial setting) is considered in the denominator of the ratio. The risk ratio is a good measure of the strength of an effect, while the risk difference is a better measure of the public health impact, because it compares the difference in absolute risk and, therefore provides an indication of how many people might benefit from an intervention. An odds ratio is the measure of association used in case-control studies. It is the ratio of the odds or disease in those with a risk factor compared to the odds of disease in those without the risk factor. When the outcome of interest is relatively uncommon (e.g., <10%), an odds ratio is a good estimate of what the risk ratio would be. The odds are defined as the ratio of the number of successes to the number of failures. All of these measures (risk difference, risk ratio, odds ratio) are used as measures of association by epidemiologists, and these three measures are considered in more detail in the module on Measures of Association in the core course in epidemiology. Confidence interval estimates for the risk difference, the relative risk and the odds ratio are described below.
A. Confidence Interval for a Risk Difference or Prevalence Difference
A risk difference (RD) or prevalence difference is a difference in proportions (e.g., RD = p1-p2) and is similar to a difference in means when the outcome is continuous. The point estimate is the difference in sample proportions, as shown by the following equation:

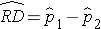
The sample proportions are computed by taking the ratio of the number of "successes" (or health events, x) to the sample size (n) in each group:

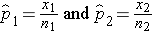 .
.
Computing the Confidence Interval for A Difference in Proportions ( p1-p2 )
The formula for the confidence interval for the difference in proportions, or the risk difference, is as follows:

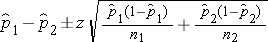
Note that this formula is appropriate for large samples (at least 5 successes and at least 5 failures in each sample). If there are fewer than 5 successes (events of interest) or failures (non-events) in either comparison group, then exact methods must be used to estimate the difference in population proportions.5
Example:
The following table contains data on prevalent cardiovascular disease (CVD) among participants who were currently non-smokers and those who were current smokers at the time of the fifth examination in the Framingham Offspring Study.
|
|
Free of CVD |
History of CVD |
Total |
|
Non-Smoker |
2,757 |
298 |
3,055 |
|
Current Smoker |
663 |
81 |
744 |
|
Total |
3,420 |
379 |
3,799 |
The point estimate of prevalent CVD among non-smokers is 298/3,055 = 0.0975, and the point estimate of prevalent CVD among current smokers is 81/744 = 0.1089. When constructing confidence intervals for the risk difference, the convention is to call the exposed or treated group 1 and the unexposed or untreated group 2. Here smoking status defines the comparison groups, and we will call the current smokers group 1 and the non-smokers group 2. A confidence interval for the difference in prevalent CVD (or prevalence difference) between smokers and non-smokers is given below. In this example, we have far more than 5 successes (cases of prevalent CVD) and failures (persons free of CVD) in each comparison group, so the following formula can be used:

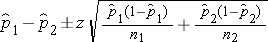
Substituting we get:

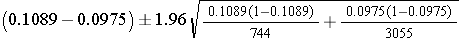
This simplifies to

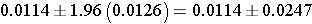
So the 95% confidence interval is (-0.0133, 0.0361),
Interpretation: We are 95% confident that the difference in proportion the proportion of prevalent CVD in smokers as compared to non-smokers is between -0.0133 and 0.0361. The null value for the risk difference is zero. Because the 95% confidence interval includes zero, we conclude that the difference in prevalent CVD between smokers and non-smokers is not statistically significant.
for the risk difference is zero. Because the 95% confidence interval includes zero, we conclude that the difference in prevalent CVD between smokers and non-smokers is not statistically significant.

A randomized trial is conducted among 100 subjects to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently used (the "standard of care"). Patients are randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery. The patients are blind to the treatment assignment. Before receiving the assigned treatment, patients are asked to rate their pain on a scale of 0-10 with high scores indicative of more pain. Each patient is then given the assigned treatment and after 30 minutes is again asked to rate their pain on the same scale. The primary outcome is a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction).
to receive either the new pain reliever or the standard pain reliever following surgery. The patients are blind to the treatment assignment. Before receiving the assigned treatment, patients are asked to rate their pain on a scale of 0-10 with high scores indicative of more pain. Each patient is then given the assigned treatment and after 30 minutes is again asked to rate their pain on the same scale. The primary outcome is a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction).
- Using the data in the table below, compute the point estimate for the difference in proportion of pain relief of 3+ points.are observed in the trial.
- Compute the 95% confidence interval for the difference in proportions of patients reporting relief (in this case a risk difference, since it is a difference in cumulative incidence).
- Interpret your findings in words.
|
Treatment Group |
n |
# with Reduction of 3+ Points |
Proportion with Reduction of 3+ Points |
|
New Pain Reliever |
50 |
23 |
0.46 |
|
Standard Pain Reliever |
50 |
11 |
0.22 |