
Measures of Disease Frequency

For centuries, knowledge about the cause of disease and how to treat or prevent it was limited by the fact that it was based almost entirely on anecdotal evidence. Significant advances occurred when the strategy for studying disease shifted to looking at groups of people and using a numeric approach to make critical comparisons.
After successfully completing this section, the student will be able to:
crude rates
category-specific rates (e.g. gender or race)
age-specific rates
morbidity rate
mortality rate
case-fatality rate
attack rate
live birth rate
infant mortality rate
autopsy rate

Video Discussion of What Variables Are (2:43)
Link to transcript of the video
A population is simply a group of people with some common characteristic, such as age, race, gender, or place of residence. A "target population" is a population for which you would like to make some conclusions. Examples:
survivors of the atomic blasts in Japan,
veterans of the Vietnam war or the Gulf Wars
members of the U.S. military who sustained a head wound while stationed in Iraq
residents of New Orleans who lost their homes during hurricane Katrina.
all babies born in Tanzania in 2012
Enrollment in an epidemiological study can also be the defining event for a person to enter a fixed population:
Persons who completed and returned a questionnaire in response to an invitation to join the Black Women's Health Study, and who were found to be eligible by study staff
Residents of Boston public housing who met eligibility criteria, completed informed consent and a baseline survey, and had one meeting with a community health worker to discuss smoking cessation
residents of any town or, state, or country
members of a health insurance plan
women who have given birth within the past 12 months


It can be a bit challenging at times to distinguish between fixed and dynamic populations, because the same description (e.g., resident of Boston) can be interpreted as an event or a current state. There are two helpful solutions to help clear up this confusion:
Ratio: A ratio is just a number that is obtained by dividing one number by another. A ratio doesn't necessarily imply any particular relationship between the numerator and the denominator. For example, if there were 100 women in this class and 20 men, the ratio of women to men would be 100/20 or 5 women for each man. This is just a simple ratio that indicates how many times larger one quantity is compared to the other.
Proportion: A type of ratio that relates a part to a whole; often expressed as a percentage (%). For example, if there are 120 women in a class of 130 students, then the proportion of women is 120/130 = 92%.
Rate: A type of ratio in which the denominator also takes into account another dimension, usually time. For example, speed is measured in miles/hour; it can be calculated by dividing the number of miles traveled by the number of hours that it took. Water flow might be quantified in gallons/minute; one might measure the number of gallons released during a period of time and divide by the number of minutes it took in order to calculate the average rate. An example of a rate that doesn't involve time is motor vehicle deaths, which are often reported as deaths/vehicle-miles. This is one way in which the relative safety of different types of transportation (automobiles, buses, trains, airplanes) can be compared.
While the term "rate" is used very broadly among the general population (birth malformation rate, autopsy rate, smoking rate, smoking rate, tax rate), in reality all these measures are proportions. For example, the smoking "rate" among adults is actually the number of adults in a population who smoke divided by the total number of adults in the population—in other words, a proportion because the numerator is a subset of the whole. One way to tell a proportion from a true rate is that a rate can never be expressed as a percentage, while a proportion should always be able to be expressed as a percentage.
Counting the people with disease is an important basic measure of disease frequency that is essential to detecting trends or the sudden occurrence of a problem, such as an epidemic. Simple counts of the number of diseased people are also important to public health planners and policy makers for assessing the need for resources in a population.
Table - New AIDS Cases by Year
|
Year |
Total AIDS Cases in City A |
|---|---|
|
2001 |
0 |
|
2002 |
1 |
|
2003 |
5 |
|
2004 |
22 |
|
2005 |
75 |
The count of AIDS cases shown here for City A would likely stimulate discussion among public officials & health providers, but count data alone don't allow us to fully understand the problem. We don't know if all of the cases were long time residents who developed AIDS while living in City A. Some may have moved into town after they developed AIDS. We also don't know whether any of the cases moved away or died.
A second limitation of just counting the number of existing cases is that it doesn't allow us to make fair comparisons of the frequency of HIV in different cities, since they don't take into account the total number of residents.
When measuring disease frequency, proportions and rates are very helpful when comparing groups, because they relate the number of people with disease to the size of the population in which they occur. Prevalence and incidence are the two fundamental measures of disease frequency.
Suppose, for example, that City A had 75 HIV+ residents, while City B had 35. This would suggest a larger problem in City A.
Table - Existing Cases of HIV+ in Cities A and B
|
|
Existing Cases |
|---|---|
|
City A |
75 |
|
City B |
35 |
However, suppose City A was substantially larger, with 30,000 residents, compared to only 7,000 in City B. To be fair, one would need to take this into account by dividing the number of cases in each city by the respective population size.
Table - HIV+ Cases, Population Size, and Prevalence in Cities A and B
|
|
Existing Cases |
Population Size |
Prevalence |
|---|---|---|---|
|
City A |
75 |
30,000 |
0.0025 |
|
City B |
35 |
7,000 |
0.0050 |
In essence, the resulting decimal fractions indicate the frequency of HIV per person in each city, and we can now see that City B actually has a higher prevalence of HIV+ residents than City A, in fact twice as high (0.005 vs. 0.0025). However, the frequency of HIV per individual is not a very intuitive or useful concept. However, if we multiply each of the results x 10,000, we have the frequency per 10,000 population. Obviously, neither city has exactly 10,000 residents, but by converting the decimal fractions to this standard population size, we can now have a more understandable description of the prevalence of HIV+ residents in each city.
|
|
Existing Cases |
Population Size |
Prevalence (as a decimal fraction) |
Prevaence (per 10,000 population) |
|---|---|---|---|---|
|
City A |
75 |
30,000 |
0.0025 |
25 per 10,000 |
|
City B |
35 |
7,000 |
0.0050 |
50 per 10,000 |





The measure of disease frequency we have calculated is the prevalence, that is, the proportion of the population that has disease at a particular time. Prevalence indicates the probability that a member of the population has a given condition at a point in time. It is, therefore, a way of assessing the overall burden of disease in the population, so it is a useful measure for administrators when assessing the need for services or treatment facilities.
Epidemiologists sometimes make a distinction between point prevalence, the proportion of the population at a 'point' in time. So it includes all previous cases who are still have the condition and are still members of the population. A good way to think about point prevalence is to imagine that you took a snapshot of the poplation and determined the proportion of people who had the condition of interest at the time the snapshot was taken.
Example: The percentage of a class reporting symptoms of seasonal allergies during the first week in May 2016.

Period prevalence is similar to point prevalence, except that the "point in time" is broader. For example, suppose that 2,477 residents of Framingham, MA were examined the establish the proportion of the population that had cataracts. It may have taken 2-3 years to conduct all of the eye exams, and when they were done the prevalence over this observation period would include people who had acquired cataracts previously if they still lived in that populations, and it would also include newl cases, i.e., those who had developed cataracts during the 2-3 year period when the eye exams were conducted. So, it can just be thought of as a wide "point in time".
Example: During 1980 the Framingham Het Study examined 2,477 subjects for cataracts and found that 310 had them. So, the prevalence was 310/2,477 = 0.125.
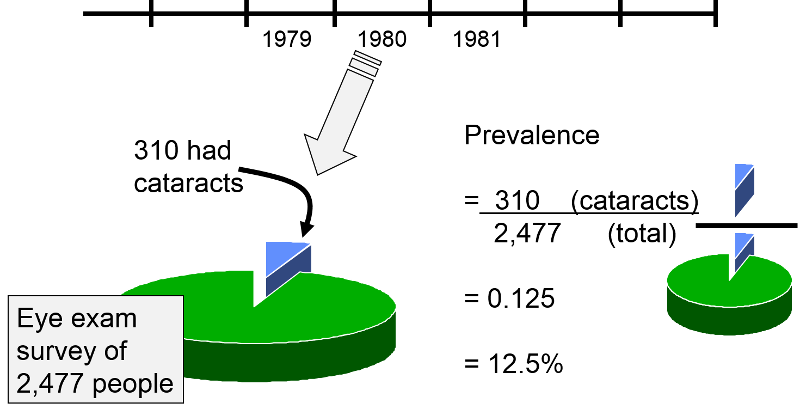
This can conveniently be expressed as 12.5 per 100 or 12.5% (per cent means 'per hundred'). Since the examination of these subjects took place over a year, it might be referred to as a period prevalence, and the numerator conceivably could include people who had first developed cataracts prior to 1980 and people who developed cataracts during 1980 just before their exam was done. Note that all people counted in the numerator are also included in the denominator, i.e., the numerator is a subset of the denominator.
Frequently, this distinction between point prevalence and period prevalence is blurry, because it is rare to be able to assess the proportion of a population that has a disease condition at exactly the same point in time. We could consider our class to be a population, and I could ask the students to raise their hand if they had an upper respiratory tract infection today. I could even take a photo and use this to visualize the prevalence of respiratory infections at this point in time. So, in this case this snapshot of disease frequency in the class would truly represent prevalence at a point in time. In most cases, however, it takes much longer than an instant to assess the proportion of a population that is diseased. In other words, we have to be flexible in our definition of a "point" in time, and we have to allow for broad points. Regardless, of this distinction between point prevalence and period prevalence, the more important concept is that prevalence is a measure of the proportion of the population that has a given disease, condition, or characteristic at a given time. We will not try to distinguish point and period prevalence in EP713.


|
Notes on Prevalence Note that we can also use prevalence to assess the frequency of behaviors or characteristics that might be risk factors for disease. Smoking isn't a disease per se; it is a risk factor. However, it is relevant to assess the prevalence of this behavior. Also, note that the "point in time" can be an event rather than a distinct calendar time. For example, many elderly men are found to have prostate cancer on autopsy, even though they were unaware of it and died for other reasons. It is appropriate to think of the frequency of prostate cancer at the time of autopsy as prevalence, even though men are having autopsies performed at many different points in calendar time. Similarly, military recruits undergo a physical examination during induction, and the exams are performed at many different times. Nevertheless, the proportion of inductees found to be colorblind during their physical exam would be the prevalence of colorblindness in young men.
|
Note that prevalence is a proportion and not a rate, although the latter term is often used. So, the terms "prevalence rate" and "autopsy rate" are technically incorrect (although commonly used).

Question: When calculating point prevalence, what should you do with people who were in the population, but they died or moved out of the population?
Answer


In contrast to prevalence, incidence is a measure of the occurrence of new cases of disease (or some other outcome) during a span of time. There are two related measures that are used in this regard: incidence proportion (cumulative incidence) and incidence rate. A useful way to think about cumulative incidence (incidence proportion) is that it is the probability of developing disease over a stated period of time; as such, it is an estimate of risk. Ken Rothman uses the example of a newspaper article that states that women who are 60 years of age have a 2% risk of dying from cardiovascular disease. As written this statement is impossible to interpret, because it doesn't specify a time period. In order to interpret risk it is necessary to know the length of time that applies. A 2% risk has a very different meaning if it is over the next 12 months vs. the next 10 years. Therefore, the incidence proportion (cumulative incidence) must specify a time period. For example, the incidence proportion of neonatal mortality is the number of deaths divided by the number of births over the first 30 days after birth.
The concept of risk is fairly intuitive - if a group of disease-free people were followed for a period of time, one could determine the proportion of people who developed the disease at some point during the observation period in order to arrive at an estimate of the probability of developing that disease, i.e. the risk. However appealing this is for its simplicity, there are some drawbacks to this approach to assessing the occurrence of health outcomes, because an accurate assessment of probability relies on observing all subjects for the entire observation period. This is particularly a problem when assessing long term risk.
For this reason, the incidence proportion is generally used in situations where the follow-up time is relatively short and there is relatively little loss to follow-up. Otherwise, epidemiologists generally use the incidence rate.
Ideally, if we are to estimate incidence (incidence proportion or incidence rate), we would want to measure this in a sample of people who are truly at risk of developing the outcome of interest. So, in measuring incidence we would like to exclude anyone who was not at risk of developing disease, because they already had the disease or because they couldn't develop it. For example, if one wanted to estimate the risk of developing uterine cancer in postmenopausal women, we ideally would like to exclude women who had previously undergone hysterectomy (removal of the uterus), since they are no longer at risk of developing this particular type of cancer.
 Suppose we were interested in the problem of diabetes in a nursing home with 800 residents. We would begin by doing blood tests on all residents to determine which were diabetic. If 50 of the residents were diabetic initially, then the prevalence of diabetes at this point in time would be 50/800 = 0.0625. The standard way of expressing this would be to say that the prevalence was 62.5 per 1000 residents or 6.25 per 100 residents, or 0.0625%
Suppose we were interested in the problem of diabetes in a nursing home with 800 residents. We would begin by doing blood tests on all residents to determine which were diabetic. If 50 of the residents were diabetic initially, then the prevalence of diabetes at this point in time would be 50/800 = 0.0625. The standard way of expressing this would be to say that the prevalence was 62.5 per 1000 residents or 6.25 per 100 residents, or 0.0625%
If we want to estimate the incidence of diabetes in this population over the next 12 months, we need to exclude the 50 people who are already diabetic and focus on the 750 residents who are disease-free initially. We would then need to do additional blood tests to determine how many new cases developed during the span of time. Because some of the residents might die or be transferred to other facilities during the year, we ideally would like to take blood tests frequently, but for financial and logistical reasons, we might simply conduct a second series of blood tests after one year. If 25 were found to be diabetic at the end of a year, then the incidence would be 25/750 = 0.0333 or about 3.3 per hundred (3.3%) over a year. Note that we are describing the time span, i.e. the period of observation, when we report the incidence.
When incidence is determined in this way, that is, by evaluating the presence of disease at the beginning and then dividing the number of known new cases by the number of people "at risk" at the beginning, it is referred to as a cumulative incidence and can also be thought of as the incidence proportion. While people commonly refer to this as a 'rate,' this is really a proportion. It is the proportion of the "at risk" group that developed disease over a stated block of time.
The cumulative incidence of AIDS in MA during 2004:
Cumulative incidence is easy to measure and is commonly used in a wide variety of circumstances. For example, if we wanted to determine the incidence of AIDS in Massachusetts during calendar year 2004, it isn't feasible for us to check every citizen at the beginning and end of the year. Census data gives us a rough idea of how many people lived in Massachusetts during 2004, and AIDS is a reportable disease, so we could go to the MA Department of Public Health and obtain an estimate of the number of people with AIDS at the beginning of the year, and we could subtract this number from the population size to get a denominator that represents the number of people "at risk" of developing AIDS. Then, we could go back to DPH at the end of the calendar year and ask how many new people had been reported with AIDS. This is our numerator. So, the cumulative incidence would be:
(# new AIDS cases reported during the year) / (population of MA at risk),
i.e. minus existing cases at the beginning of the year)
In reality, there were 523 new AIDS cases reported in MA in 2004, and the population was about 5.7 million. So, the cumulative incidence was about 9.2 per 100,000 people during 2004. Note that the denominator is just an estimate based on the last census. In reality, people were being added to and subtracted from the population continually as a result of births, deaths, moving into the city, and moving out. We also didn't take into account exactly when they developed AIDS, although we probably don't care whether they developed it earlier or later within a one year period. Nevertheless, this cumulative incidence is a useful number, and it is relatively easy to get the information we need to calculate it.
It is important to specify the time period when reporting cumulative incidence. In the fall semester of 2003 there were 130 students in EP713 at the beginning of the semester, and 55 of them reported developing a cold or other respiratory infection during the semester. So, the cumulative incidence = 55/130 = 0.42307 or 42.3% over the course of the semester. The time period of observation is expressed in words.
Remember that a rate almost always contains a dimension of time. Therefore, the incidence rate is a measure of the number of new cases ("incidence") per unit of time ("rate"). Compare this to the cumulative incidence (incidence proportion), which measures the number of new cases per person in the population over a defined period of time. Because studies of incidence in epidemiology are conducted among groups of people as they move through time, the denominator is actually a combination of the number of people and the amount of time. This is expressed as person-time. The time units can be expressed in days, months, or years, but should be tied to the length of the study and aid interpretation of the results. The most frequently encountered expression is "person-years". The characteristics of cumulative incidence and incidence rate are illustrated in the examples below.
Note: While we generally refer to cumulative incidence (incidence proportion) and incidence rate as measures of disease frequency, they can be applied to any sort of occurrence. For example, treatments to cure or relieve disease conditions are also measured using the incidence proportion or rate, as we will see in the example below. The key thing to keep in mind is that either measure of incidence (unlike prevalence) measures a transition from one state to another: well to sick, sick to well, alive to dead, unborn to born, etc.
A comparison of pain relief with two analgesics:
Suppose you were asked to analyze the data from a small preliminary clinical trial with 20 subjects. All subjects had a comparable degree of knee pain from osteoarthritis, and they were being compared with respect to pain relief after receiving a standard pain medication (Drug B) or a new pain medication (Drug A). The 20 patients were randomly assigned to one drug or the other, and there were ten subjects in each group. After receiving the medication, the investigators checked on the subjects at hourly intervals to see if the subjects had had relief of pain. For each subject, the time at which pain relief occurred was recorded. Results are illustrated in the graph below. Link to a text description of the results
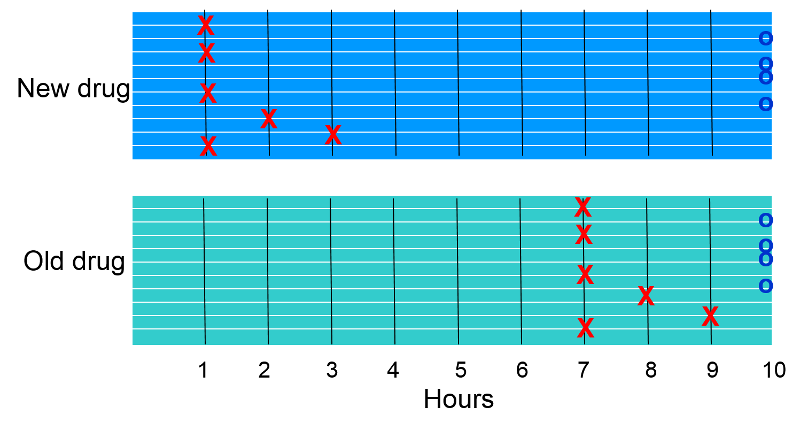
The "X"s indicate when subjects reported pain relief. The "O"s at the end indicate subjects who did not report relief of pain.
Six of ten subjects in each group experienced relief of pain, so the cumulative incidence of pain relief was 6/10 = 60% in each group. Whenever cumulative incidence is determined, one determines the proportion of subjects who experienced the outcome of interest during a block of time, without taking into account when subjects developed the outcome. Visually, however, it is clear that if we consider when subjects experienced relief, the rate was greater in the subjects receiving the new drug.
In this hypothetical study all subjects were observed for a maximum of 10 hours, and some did not achieve pain relief, while others got relief after varying periods of time. We can calculate the average rate of pain relief in each group by adding up the duration of pain for subjects in each group and dividing by the number of subjects in each group.
In the group receiving the new drug the times were 4x1 + 2 + 3+ 4x10= 49 hours for the group (person-hours). So the incidence rate of relief was 6/49 person-hours or on average 12.2 per 100 person-hours of observation. Note that once a subject experiences the outcome of pain relief, they are no longer considered to be under observation.
In the group receiving the old drug the times were 4x7 + 8 + 9 + 4x10= 85 hours for the group (person-hours). So the incidence rate of relief was 6/85 person-hours or on average 7.0 per 100 person-hours of observation. So, the rate of pain relief was greater in the group receiving the new drug.
What we have calculated is the incidence rate. This is a true rate, because time is an integral part of the calculation, analogous to miles per hour (a rate of speed) or gallons per minute (a rate of flow).
Several things are noteworthy about this incidence rate.

Question: A participant in a prospective cohort study or a randomized clinical trial stops contributing additional "disease-free observation time" when they develop the outcome of interest or become lost to follow-up for any reason (death, failure to respond to phone calls, letters and emails, etc.). Does this mean that they are no longer in the study?
Answer
Incidence of HIV in a Brothel
A follow-up study was conducted to determine which sexual behaviors were associated with the greatest risk of becoming HIV+. The study was conducted in a group of female prostitutes. The subjects were tested prior to the beginning of the study, and five HIV+ women were excluded. The the remaining ten women were followed for six years beginning in January 1989. Each woman was contacted and retested at the beginning of January each year. The table below summarizes the findings these ten subjects. A circled plus sign (+) indicates when a subject was found to be HIV+; a question mark (?) indicates when a subject became lost to follow-up. The dashed lines indicate continued follow-up.
Link to a detailed description of the table below
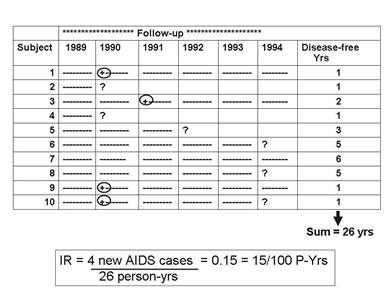
The cumulative incidence was 4/10=40% over six years, but this doesn't take into account the different amounts of time contributed by those who didn't become HIV positive, one of whom (Subject #7) was followed throughout the six years of the study, but the remainder of whom were lost to follow-up sometime before the end of the study (Subjects #2, 4, 5, 6, 8).
The incidence rate, however, can take these problems into account, because the denominator is the total "at risk" observation time contributed by all ten subjects. The column at the far right indicates each subject's "at risk" observation time, and the sum for the ten subjects was 26 years. So, the IR= 4/26 person-yrs = 0.15/person-year = 15/100 person-years of observation.
Note that person-time stopped being counted as soon as the subject was found to be HIV positive, because the subject was no longer "at risk" of developing the outcome—they already had experienced it. For example, Subject #1 contributed one person-year even though she was followed for all six years.
Incidence rates are often computed in prospective cohort studies (e.g., The Framingham Heart Study or The Nurses Health Study) and randomized clinical trials (e.g., The Physician's Health Study, which looked at the effect of low-dose aspirin on heart disease). It is more accurate than cumulative incidence, but it requires repeated follow-up observations on each subject, and studies like this can be very expensive and time consuming.
Also consider that subjects are sometimes recruited into studies at different times. Each subject's disease-free observation time or "at risk" time can be calculated as the time from their entry into the study until a) they get the disease, b) they become lost to follow-up, or c) the study ends.
For example, consider a hypothetical clinical trial that was conducted to determine whether taking low-dose aspirin reduced the frequency of heart attacks in middle-aged and elderly men. The time line below summarizes events 12 subjects labeled 1-12, all of whom were allocated to the placebo-treated group.
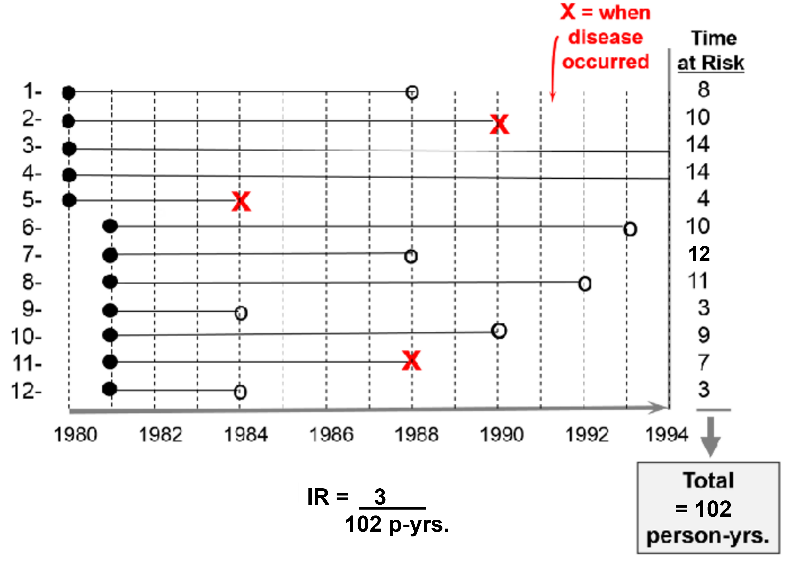
The first 5 subjects were enrolled in 1980, and the next 7 subjects were enrolled one year later. All subjects began taking aspirin upon enrollment. Therefore their "exposure" to aspirin began upon enrollment as indicated by the solid black dots.
The red "X"s indicate when subjects had a heart attack; their exposure time at risk ends there, since having a first heart attack means that they were no longer at risk of having a first heart attack; they had the outcome of interest at that point. Subject #2 had a heart attack in 1990; subject #5 had one in 1984; subject #11 had one in 1988.
The open circles indicated six subjects who were lost to follow-up. They stopped responding to all requests for follow up after that point. We know that they had not had a heart attack up to that point, but we don't know what happened to them after that, so they stop contributed observed exposure time at risk. Subject #1 was lost to follow up in 1988; #6 was lost in 1993; #7 was lost in 1988; #8 was lost in 1992; #9 was lost in 1984;
All of this information can be taken into account in order to compute the average rate at which heart attacks occur in this group of 12 men being treated with low-dose aspirin. We can do this in a way that is analogous to example #2 above. There were 3 heart attacks, and we divide this by the total amount of time that the men were exposed and at risk of developing a heart attack. For each man the exposure time at risk is the time from their entry into the study until one of three endpoints: a) the disease occurs, b) the subject is lost to follow-up, or c) the study concludes. The exposure time at risk for each man is shown in the column at the far right of the figure, and if we add these, the total exposure time for the group was 102 years. Therefore, the average rate at which the outcome occurred was 3/ 102 person-years of observed exposure time.
Example: Incidence Rate in the Nurse's Health Study - Estrogens and Coronary Artery Disease
Data collected from the Nurses' Health Study, a prospective cohort study, was used to compare rates of coronary artery disease in post-menopausal women using hormone replacement therapy (HRT) and post-menopausal women who had not used HRT. The data was summarized in the table below.
|
|
Coronary Artery Disease |
Person-Years of Disease Free Observation |
|---|---|---|
|
Used HRT |
30 |
54,308.7 |
|
No Use of HRT |
60 |
51,477.5 |
Women on postmenopausal hormones had an incidence rate of 30 events during 54,308.7 person years of follow-up, or 55.2 / 100,000 person-years. Women in the untreated group had 60 events during 51,477.5 person-years of follow-up - an incidence rate of 116.6 / 100,000 person-years.
Another Example: Incidence Rate in the Nurse's Health Study – Obesity and Myocardial Infarction
In this study, incidence rates of MI (myocardial infarction) were compared among five groups of women based on their body mass index (BMI). There were certainly different numbers of women in the five groups, but for each group they computed the incidence rate by counting the number who developed MI and dividing by the group's total "at risk" time of observation. The result was then converted to the number per 100,000 person-years to facilitate comparison among the five groups.
|
Body Mass Index (BMI) |
# Non-fatal Myocardial Infarctions |
Person-Years of Observation |
Incidence Rate per 100,000 Person-Years |
|---|---|---|---|
|
<21 |
41 |
177,356 |
23.1 |
|
21.0-22.9 |
57 |
194,243 |
29.3 |
|
23.0-24.9 |
58 |
155,717 |
36.0 |
|
25.0-29.9 |
67 |
148,541 |
45.1 |
|
>30 |
85 |
99,573 |
85.4 |
By convention, all three measures of disease frequency (prevalence, cumulative incidence, and incidence rate) are expressed as some multiple of 10 in order to facilitate comparisons. Consider these three examples:
One can express the final result as the number of cases per 100 people, or per 1,000 people, or per 10,000 people, or per 100,000. Generally one uses a convenient multiple of ten. For example, the expressions below are all equivalent, but the last two are the most convenient to talk about & think about. Note: Each time you move the decimal to the right, you increase the number by a factor of 10.
|
Equivalent Expressions of Disease Frequency 0.00232 new cases per 1 person-yrs. 0.0232 new cases per 10 person-yrs. 0.232 new cases per 100 person-yrs. 2.32 new cases per 1,000 person-yrs. 23.2 new cases per 10,000 person-yrs. 232 new cases per 100,000 person-yrs.
|
 Common Pitfall: A common mistake among beginning students is to fail to specify the dimensions after calculating incidence, especially for cumulative incidence.
Common Pitfall: A common mistake among beginning students is to fail to specify the dimensions after calculating incidence, especially for cumulative incidence.
|
Prevalence (a proportion) = People # People with disease at a point in time Total People # People in the study population
Cumulative Incidence (a proportion) = People # new cases in a specified period Total People # People (at risk) in the study population
Incidence Rate (a rate) = People # new cases of disease People-Time Total observation time in a group at risk |


Cumulative incidence (the proportion of a population at risk that will develop an outcome in a given period of time) provides a measure of risk, and it is an intuitive way to think about possible health outcomes. An incidence rate is less intuitive, because it is really an estimate of the instantaneous rate of disease, i.e. the rate at which new cases are occurring at any particular moment. Incidence rate is therefore more analogous to the speed of a car, which is typically expressed in miles per hour. Time has to elapse to measure a car's speed, but we don't have to wait a whole hour; we can glance at the speedometer to see the instantaneous rate of travel. Rather than measuring risk per se, incidence rate measures the rate at which new cases of disease occur per unit of time, and time is an integral part of the calculation of incidence rate. In contrast, cumulative incidence or risk assesses the probability of an event occurring during a stated period of observation. Consequently, it is essential to describe the relevant time period in words when discussing cumulative incidence (risk), but time is not an integral part of the calculation. Despite this distinction, these two ways of expressing incidence are obviously related, and incidence rate can be used to estimate cumulative incidence. At first glance it would seem logical that, if the incidence rate remained constant the cumulative incidence would be equal to the incidence rate times time:
CI = IR x T
This relationship would hold true if the population were infinitely large, but in a finite population this approximation becomes increasingly inaccurate over time, because the size of the population at risk declines over time. Rothman uses the example of a population of 1,000 people who experience a mortality rate of 11 deaths per 1,000 person-years over a period of years; in other words, the rate remains constant. The equation above would lead us to believe that after 50 years the cumulative incidence of death would be CI = IR X T = 11 X 50 = 550 deaths in a population which initially had 1,000 members. In reality, there would only be 423 deaths after 50 years. The problem is that the equation above fails to take into account the fact that the size of the population at risk declines over time. After the first year there have been 11 deaths, and the population now has only 989 people, not 1,000. As a result, the equation above overestimates the cumulative incidence, because there is an exponential decay in the population at risk. A more accurate mathematical expression that takes this into account is:
CI = 1 - e(-IR x T), where 'e' = 2.71828
This constant 'e' arises in many mathematical relationships describing growth or decay over time. If you are using an Excel spreadsheet, you could calculate the CI using the formula:
CI = 1 - EXP(-IR xT)
In the graph below the upper blue line shows the predicted number of deaths using the approximation CI = IR x T. The lower line, in red, shows the more accurate projection of cumulative deaths using the exponential equation.
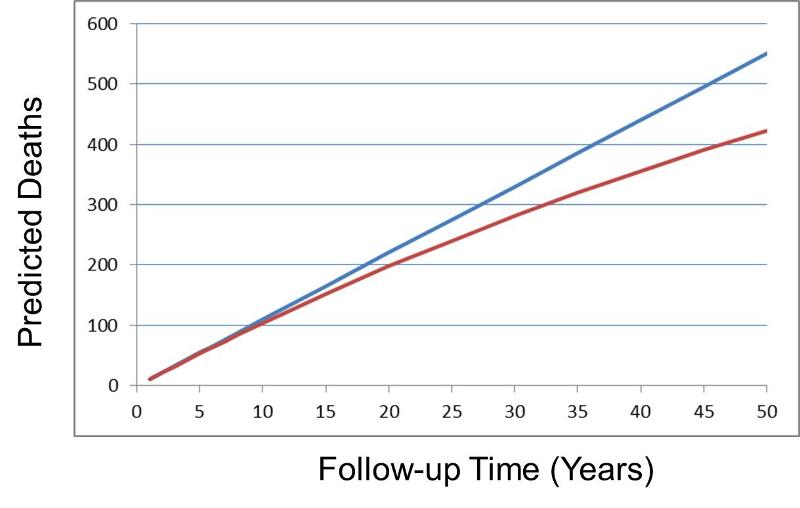
Nevertheless, note that the prediction from CI = IR x T gives quite reasonable estimates as long as the cumulative incidence remains less than 10% (equivalent to 100 deaths in the population of 1,000 in the above graph).
(Optional)
The equation CI = IR x T provides a reasonable estimate of risk when the incidence rate is relatively constant, but this isn't always the case. When the incidence rate changes over time there are other options for estimating risk.
Table - Life-table for Death from Motor-vehicle Injury from Bitth through Age 85
|
Age (years) |
Mortality Rate per 100,000 person-years |
At Risk |
Deaths in Interval |
Risk |
Survival Probability |
Cumulative Survival Probability |
|---|---|---|---|---|---|---|
|
0-14 |
4.7 |
100,000 |
70.5 |
0.000705 |
0.999295 |
0.999295 |
|
15-24 |
35.9 |
99,930 |
358.1 |
0.003584 |
0.996416 |
0.995714 |
|
25-44 |
20.1 |
99,571 |
399.5 |
0.004012 |
0.995988 |
0.991719 |
|
45-64 |
18.4 |
99,172 |
364.3 |
0.003673 |
0.996327 |
0.988077 |
|
65-84 |
21.7 |
98,808 |
427.9 |
0.004331 |
0.995669 |
0.983798 |
Adapted from Iskrant and Joliet
In this hypothetical example, the initial population at risk was arbitrarily set at 100,000, and the mortality rates in each group (column 2, mortality rates=deaths per 100,000 person-yrs.) were used to calculate the number of deaths among those remaining at risk for each interval using the formula CI = IR x T. Thus, the first age group spanned 15 years and the mortality rate was 4.7/100,000 person-years, so the number of deaths was 4.7 x 15 = 70.5.
The illustration below shows the results of analysis of a trial looking at the ability of zidovudine (an anti-retroviral drug used in the treatment and prevention of HIV) to reduce maternal to child transmission. Pegnant women with mildly symptomatic HIV disease and no prior treatment with antiretroviral drugs during the pregnancy, were randomly assigned to one of two regimens: 1) a regimen consisting of zidovudine given ante partum and intra partum to the mother and to the newborn for six weeks or 2) placebo.
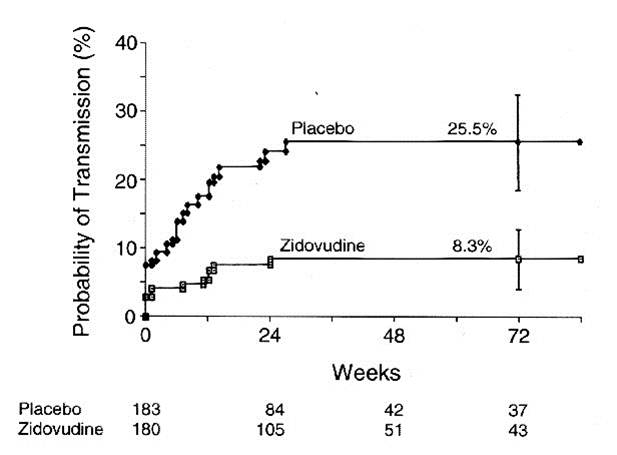
The graph shows that about 8 % of the infants in the placebo group tested HIV+ at birth, and the probability of HIV transmission in this group rose to 25.5% by 72 weeks of age. Infants in the zidovudine group only had about a 3% probablility of being born HIV+, and their risk of transmission only todr yo 8.3% by 72 weeks of age. (The data are from Connor EM, et al.: Reduction in maternal-infant transmission of human immunodeficiency virus type 1 with zidovudine treatment. N. Engl. J. Med. 1994;331:1173-1180, as quoted in the textbook by Aschengrau and Seage in Table 7-5, page 191 in the 2nd edition.) This was part of protocol 076 that originally demonstrated the efficacy of zidovudine in women in the United States and France. The illustration below shows Kaplan-Meier plots of the probability of HIV transmission for the two groups. The estimated percentages of infants infected at 72 weeks are shown with 95 percent confidence intervals. The numbers of infants at risk at 24, 48, and 72 weeks are shown below the figure.


Prevalence is the proportion of a population that has a condition at a specific time, but the prevalence will be influenced by both the rate at which new cases are occurring and the average duration of the disease. Incidence reflects the rate at which new cases of disease are being added to the population (and becoming prevalent cases). Average duration of disease is also important, because the only way you can stop being a prevalent case is to be cured or to move out of the population or die. For example, about a decade ago the average duration of lung cancer was about six months. Therapy was ineffective and almost all lung cancer cases died. From the time of diagnosis, the average survival was only about six months. So, the prevalence of lung cancer was fairly low. In contrast, diabetes has a long average duration, since it can't be cured, but it can be controlled with medications, so the average duration of diabetes is long, and the prevalence is fairly high.
If the population is initially in a "steady state," meaning that prevalence is fairly constant and incidence and outflow [cure and death] are about equal), then the relationship among these three parameters can be described mathematically as:
P/(1-P) = IR x Avg. Duration,
where P= proportion of the population with the disease and (1-P) is the proportion without it, IR is the incidence rate, and Avg. Duration is the average time that people have the disease (from diagnosis until they are either cured or die). If the frequency of disease is rare (i.e., <10% of the population has it), then the relationship can be expressed as follow:
Prevalence = (Incidence Rate) x (Average Duration of Disease)
The relationship can be visualized by thinking of inflow and outflow from a reservoir. The fullness of the reservoir can be thought of as analogous to prevalence. Raindrops might represent incidence or the rate at which new cases of a disease are being added to the population, thus becoming prevalent cases. Water also flows out of the reservoir, analogous to removal of prevalent cases by virtue of either dying or being cured of the disease. Imagine that incidence (rainfall) and the rate of cure or death are initially equal; if so, the height of water in the reservoir will remain constant.
This relationship can also be used to calculate the average duration of disease under steady state circumstances. If Prevalence = (Incidence) X (Average Duration), then it follows that
Average Duration = (Prevalence) / (Incidence)
Example: Suppose the incidence rate of lung cancer is 46 new cancers per 100,000 P-Y, and the prevalence is 23 per 100,000 population, then
Average Duration of Disease = (23/100,000 persons / 46/100,000 person-years = 0.5 year
Conclusion: Individuals with lung cancer survived an average of 6 months from the time of diagnosis to death.




Prevalence and incidence are the fundamental measures of disease frequency, but special names have evolved for these measures, depending on their specific use. All of these tend to be referred to as rates, even though, strictly speaking, they often refer to proportions (cumulative incidence or prevalence).
Either prevalence or incidence can be broken down into categoies, e.g., age groups, or by gender, or race, or some combination of these. For example, since disease frequency often differs substantially with age, one frequently sees "age-specific" rates of disease.
Example 1: A table of age-specific rates of stroke (incidence)
|
Age Group |
# New Occurrences |
Group Size |
Cumulative Incidence per 100,000 persons |
|---|---|---|---|
|
0-34 |
0 |
582,083 |
0 |
|
35-44 |
28 |
113,581 |
25 |
|
45-54 |
114 |
114,208 |
100 |
|
55-64 |
320 |
91,484 |
350 |
|
65-74 |
550 |
81,155 |
900 |
|
75+ |
1.126 |
37,531 |
3,000 |
Example 2: A Table of race-specific causes of death per 100,000 population (mortality rates, i.e., incidence) in the US, 1967
|
|
White |
Black |
|---|---|---|
|
Hypertension |
21.1 |
68.6 |
|
Homicide |
3.5 |
32.3 |
|
Diabetes mellitus |
16.6 |
28.9 |
|
Tuberculosis |
2.5 |
9.6 |
|
Suicide |
11.3 |
5.7 |
|
Leukemia |
7.4 |
5.5 |
|
Syphilis |
1.0 |
3.0 |
Morbidity rate is the incidence of non-fatal cases of a disease in a population during a specified time period. For example, during 1982 there were 25,520 non-fatal cases of TB in the US population. The mid-year population was estimated at 231,534,000. Therefore, the
Morbidity rate of TB =25,520/231,534,000 = 11.0/100,000 over one year
Note that this is a cumulative incidence and therefore is really a proportion, not a true rate.)
Mortality Rate: In 1982 there were 1,807 deaths from TB in the US population, so the mortality rate for TB was 7.8 per million over one year (also a cumulative incidence, not a true rate).
Case-Fatality Rate: the number of deaths from a specific disease divided by the total number of cases of that disease, i.e. the proportion of fatal cases of a disease (%). This provides a measure of the severity of the disease.
Example: Reyes Syndrome is a rare, but highly fatal disease in which the liver and brain become dysfunctional due to abnormal accumulation of cellular fat. It tends to occur when people are recovering from a viral illness, and it tends to be associated with use of aspirin, especially in children. If there were 200 cases of Reyes syndrome in 1982 and 70 died, then the case-fatality rate would be 70/200 = 35% over one year.
[Note: This is generally calculated by dividing the deaths reported in a given year by the number of cases reported in the same year, but this can be misleading since some diseases (e.g., TB) aren't rapidly fatal. Thus, many of the TB fatalities that occurred in 1982 were due to cases diagnosed several years earlier.]
Attack Rate: a cumulative incidence for a disease during a specific period (e.g., an epidemic).
Example: After a church picnic in Oswego, NY many attendees got food poisoning. There were 75 people at the picnic; 46 got sick within several hours, so the attack rate was 46/75 = 61%.
Live birth rate: the frequency of live births in one year per 1,000 females of childbearing age.
Infant Mortality Rate: the frequency of deaths in children under 1 year of age occurring during a one year period per 1,000 live births.
These are often incorrectly referred to as incidences or rates, but they are, in fact, proportions..
Autopsy Rate: the proportion of people who have a particular finding on a postmortem exam (the prevalence of a certain finding among the population of people who get autopsied).
Birth Defect Rate: the prevalence of a congenital abnormality at the "point" of birth. The denominator can be either live births or total births (which includes live births + stillbirths), but it generally does not include spontaneously aborted fetuses.

Questions to test your understanding



A sample of 100 middle aged and elderly women was followed prospectively for 10 years in order to study rates of ovarian cancer. All subjects entered the study on January 1, 1990, and all were free of cancer at the beginning. All women were followed until December 31, 1999. None were lost to follow-up. During this period, five subjects were diagnosed with ovarian cancer, but they all survived to the end of the study.
Case #1 was diagnosed with ovarian cancer in January 1991.
Case #2 was diagnosed in January 1992.
Case #3 was diagnosed in January 1993.
Case #4 was diagnosed in January 1986.
Case #5 was diagnosed in January 1996.
The time at which these 5 subjects developed cancer is shown in this table:
Use this information and the information in the table below to answer the questions beneath the tabl:
|
Subject |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|---|---|---|---|---|---|---|---|---|---|---|
|
Case #1 |
|
cancer |
|
|
|
|
|
|
|
|
|
Case #2 |
|
|
cancer |
|
|
|
|
|
|
|
|
Case #3 |
|
|
|
cancer |
|
|
|
|
|
|
|
Case #4 |
|
|
|
|
|
|
cancer |
|
|
|
|
Case #5 |
|
|
|
|
|
|
|
|
cancer |
|






Use this information and the information in the table below to answer the questions beneath the table:
In January of 1990, 1,010 young adults offered to participate in a 10-year prospective study to determine their risk of Type-I diabetes. This group underwent an initial blood test to determine whether they were diabetic, and eligible subjects were re-tested yearly for the next 10 years. Among the group that offered to join the study:
? = Lost to follow-up + = Blood test positive for diabetes ------ = Continued disease-free follow-up
|
Subject # |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|---|---|---|---|---|---|---|---|---|---|---|
|
1 |
------ |
------ |
+ |
|
|
|
|
|
|
|
|
2 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
+ |
|
3 |
------ |
------ |
------ |
------ |
------ |
------ |
------ |
+ |
|
|
|
4 |
------ |
+ |
|
|
|
|
|
|
|
|
|
5 |
------ |
------ |
------ |
------ |
+ |
|
|
|
|
|
|
6 |
------ |
------ |
+ |
|
|
|
|
|
|
|
|
7 |
------ |
------ |
------ |
------ |
? |
|
|
|
|
|
|
8 |
------ |
------ |
------ |
------ |
------ |
? |
|
|
|
|





