
Bias

Before concluding that an individual study's conclusions are valid, one must consider three sources of error that might provide an alternative explanation for the findings. These are:
If a determination is made that the findings of a study were not due to any one of these three sources of error, then the study is considered internally valid. In other words, the conclusions reached are likely to be correct for the circumstances of that particular study. This does not not necessarily mean that the findings can be generalized to other circumstances (external validity). For example, the Physicians' Health Study concluded that aspirin use reduced the risk of myocardial infarction in adult male physicians in the United States. The study was carefully done, and the study was internally valid, but it was not clear that the results could be extrapolated to women, or even to non-physicians (whose risk of myocardial infarction is generally lower than that of the population overall). However, internally validity must be established before one can consider whether the results are externally valid. Therefore, investigators must first ensure that a study is internally valid, even if that means that the generalizability of the findings will be compromised.
In contrast to random error, bias refers to systematic errors in any type of epidemiologic study that result in an incorrect estimate of the association between exposures and outcomes. Investigators can introduce bias into a study as a result of the procedures for identifying and enrolling subjects or from the procedures for collecting or analyzing information. Bias can also be introduced by errors in classification of outcomes or exposures. It is important for investigators to be mindful of potential biases in order to reduce their likelihood when they are designing a study, because once bias has been introduced, it cannot be removed. The two major types of bias are:
In addition, many epidemiologists think of confounding as a type of bias. While confounding also produces incorrect estimates of the association, one can often adjust for confounding in the analysis in order to remove its distorting effects to obtain a more accurate measure of association. The problem of confounding will be addressed in a separate module.
When reading a study, one should be aware of potential biases that might have affected the conclusions and be able to predict what effect a given bias would be expected to have on the estimate of effect.
After successfully completing this unit, the student will be able to:

Selection bias can result when the selection of subjects into a study or their likelihood of being retained in the study leads to a result that is different from what you would have gotten if you had enrolled the entire target population. If one enrolled the entire population and collected accurate data on exposure and outcome, then one could compute the true measure of association. We generally don't enroll the entire population; instead we take samples. However, if one sampled the population in a fair way, such the sampling from all four cells was fair and representative of the distribution of exposure and outcome in the overall population, then one can obtain an accurate estimate of the true association (assuming a large enough sample, so that random error is minimal and assuming there are no other biases or confounding). Conceptually, this might be visualized by equal sized ladles (sampling) for each of the four cells.
|
Fair Sampling |
Diseased |
Non-diseased |
|---|---|---|
|
Exposed |
|
|
|
Non-exposed |
|
|
However, if sampling is not representative of the exposure-outcome distributions in the overall population, then the measures of association will be biased, and this is referred to as selection bias. Consequently, selection bias can result when the selection of subjects into a study or their likelihood of being retained in a cohort study leads to a result that is different from what you would have gotten if you had enrolled the entire target population. One example of this might be represented by the table below, in which the enrollment procedures resulted in disproportionately large sampling of diseased subject who had the exposure.
|
Selection Bias |
Diseased |
Non-diseased |
|---|---|---|
|
Exposed |
|
|
|
Non-exposed |
|
|
There are several mechanisms that can produce this unwanted effect:
In a case-control study selection bias occurs when subjects for the "control" group are not truly representative of the population that produced the cases. Remember that in a case-control study the controls are used to estimate the exposure distribution (i.e., the proportion having the exposure) in the population from which the cases arose. The exposure distribution in cases is then compared to the exposure distribution in the controls in order to compute the odds ratio as a measure of association.
In the module on Overview of Analytic Studies and in the module on Measures of Association we considered a rare disease in a source population that looked like this:
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
7 |
1,000 |
1,007 |
|
Non-exposed |
6 |
5,634 |
5,640 |
Given the entire population, we could compute the risk ratio = 6.53. However, one often conducts a case-control study when the outcome is rare like this, because it is much more efficient. Consequently, in order to estimate the risk ratio we could use the relative distribution of exposure in a sample of the population, provided that these controls are selected by procedures such that the sample provides an accurate estimate of the exposure distribution in the overall population.
If a control sample was selected appropriately, i.e. such that is was representative of exposure status in the population, then the case-control results might look like the table below.
|
|
Cases |
Controls |
|---|---|---|
|
Exposed |
7 |
10 |
|
Non-exposed |
6 |
56 |
Note that the sample of controls represents only 1% of the overall population, but the exposure distribution in the controls (10/56) is representative of the exposure status in the overall population (1,000/5,634). As a result, the odds ratio = 6.53 gives an unbiased estimate ratio of the risk ratio.
In contrast, suppose that in the same hypothetical study controls were somewhat more likely to be chosen if they had the exposure being studied. The data might look something like this:
|
|
Cases |
Controls |
|---|---|---|
|
Exposed |
7 |
16 |
|
Non-exposed |
6 |
50 |
Here we have the same number of controls, but the investigators used selection procedures that were somewhat more likely to select controls who had the exposure. As a result, the estimate of effect, the odds ratio, was biased (OR = 3.65).
Conceptually, the bias here might be represented by the table below in which the large ladle indicates that non-diseased subjects with the exposure were over sampled.
|
Selection Bias |
Diseased |
Controls |
|---|---|---|
|
Exposed |
|
|
|
Non-exposed |
|
|
Depending on which category is over or under-sampled, this type of bias can result in either an underestimate or an overestimate of the true association.
Example:
A hypothetical case-control study was conducted to determine whether lower socioeconomic status (the exposure) is associated with a higher risk of cervical cancer (the outcome). The "cases" consisted of 250 women with cervical cancer who were referred to Massachusetts General Hospital for treatment for cervical cancer. They were referred from all over the state. The cases were asked a series of questions relating to socioeconomic status (household income, employment, education, etc.). The investigators identified control subjects by going from door–to-door in the community around MGH from 9:00 AM to 5:00 PM. Many residents are not home, but they persist and eventually enroll enough controls. The problem is that the controls were selected by a different mechanism than the cases (immediate neighborhood for controls compared to statewide for cases), AND the door-to-door recruitment mechanism may have tended to select individuals of different socioeconomic status, since women who were at home may have been somewhat more likely to be unemployed. In other words, the controls were more likely to be enrolled (selected) if they had the exposure of interest (lower socioeconomic status).

Epidemiologists sometimes use the "would" criterion" to test for the possibility of selection bias; they ask "If a control had had the disease, would they have been likely to be enrolled as a case?" If the answer is 'yes', then selection bias is unlikel
Selection bias can be introduced into case-control studies with low response or participation rates if the likelihood of responding or participating is related to both the exposure and the outcome.
Table 10-4 in the Aschengrau and Seage text shows a scenario with differential participation rates in which diseased subjects who had the exposure had a participation rate of 80%, which the other three categories had participation rates of 60%. This might be depicted as follows:
|
Selection Bias |
Diseased |
Non-diseased |
|---|---|---|
|
Exposed |
|
|
|
Non-exposed |
|
|

Question: Can self-selection bias occur in prospective cohort studies? Reflect on your answer before you look at the answer below.
Answer
Aschengrau and Seage give an example in which investigators conducted a case-control study to determine whether use of oral contraceptives increased the risk of thromboembolism. The case group consisted of women who had been admitted to the hospital for venous thromboembolism. The controls were women of similar age who had been hospitalized for unrelated problems at the same hospitals. The interviews indicated that 70% of the cases used oral contraceptives, but only 20% of the controls used them. The odds ratio was 10.2, but in retrospect, this was an overestimate. There had been reports suggesting such an association. As a result, health care providers were vigilant of their patients on oral contraceptives and were more likely to admit them to the hospital if they developed venous thrombosis or any signs or symptoms suspicious of thromboembolism. As a result the study had a tendency to over sample women who had both the exposure and the outcome of interest.
|
Selection Bias |
Diseased |
Non-diseased |
|---|---|---|
|
Exposed |
|
|
|
Non-exposed |
|
|
Aschengrau and Seage suggest that this selection bias could have been minimized by more restrictive case selection criteria, such that only women who clearly required hospitalization would be enrolled in the case group.
Factors affecting enrollment of subjects into a prospective cohort study would not be expected to introduce selection bias. In order for bias to occur, selection has to be related to both exposure and outcome. Subjects are enrolled in prospective cohort studies before they have experienced the outcome of interest. Therefore, while it is easy to see how enrollment might be related to exposure (exposed might be more or less likely to enroll), it is difficult to imagine how either investigators or enrollees could be influenced by awareness of an outcome that hasn't yet occurred.
This form of selection bias could be more common in a retrospective cohort study, especially if individuals have to provide informed consent for participation. Since a retrospective cohort study starts after all cases of disease have occurred, subjects generally would know both their exposure and outcome status. It is not hard to imagine that those with the most interest in participation would both have been exposed and have the disease, a dynamic that would only be accentuated if the study question were a controversial one and/or there were potential liability and monetary consequences tied to the results of the study. Another less common mechanism of selection bias in a retrospective cohort study might occur if retention or loss of records of study subjects (e.g., employment, medical) were related to both exposure and outcome status.
Selection bias can occur if selection or choice of the exposed or unexposed subjects in a retrospective cohort study is somehow related to the outcome of interest.
Example:
Consider a hypothetical investigation of an occupational exposure (e.g., an organic solvent) that occurred 15-20 years ago in factory. Over the years there were suspicions that working eith the solvent led to adverse health events, but no definitive data existed. Eventually, a retrospective cohort study was conducted using the employee health records. If all records had been retained the results might have looked like those shown in the first contingency table below.
|
Unbiased Results |
Diseased |
Non-diseased |
Totaal |
|---|---|---|---|
|
Solvent exposure |
100 |
900 |
1000 |
|
Unexposed |
50 |
950 |
1000 |
This unbiased data would give a risk ratio as follows:
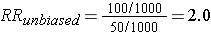
However, suppose that many of the old records had been lost or discarded, but,given the suspicions about the effects of the solvent, the records of employees who had worked with the solvents and subequently had health problems were more likely to be retained. Consequently, record retention was 99% among workers who were exposed and developed health problems, but recorded retention was only 80% for all other workers. This scenario would result in data shown in the next contingency table.
|
Biased Results |
Diseased |
Non-diseased |
Totaal |
|---|---|---|---|
|
Solvent exposure |
99 |
720 |
819 |
|
Unexposed |
40 |
760 |
800 |
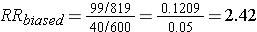
Differential loss of records results in selection bias and an overestimate of the association in this case, although depending on the scenario, this type of selection bias could also result in an underestimate of an associaton.
Prospective cohort studies will not have selection bias as they enroll subjects, because the outcomes are unknown at the beginning of a prospective cohort study. However, prosective cohort studies may have differential retention of subjects over time that is somehow related to exposure status and outcome, and this differential loss to follow up is also a type of selection bias that is analagous to what we saw above in the retrospective study on solvents in a factory..
As noted above, the enrollment of subjects will not bias a prospective cohort study, because the outcome has not yet occurred. Therefore, choice cannot be related to both exposure status and outcome status. However, retention of subjects may be differentially related to exposure and outcome, and this has a similar effect that can bias the results, causing either an overestimate or an underestimate of an association. In the hypothetical cohort study below investigators compared the incidence of thromboembolism (TE) in 10,000 women on oral contraceptives (OC) and 10,000 women not taking OC. TE occurred in 20 subjects taking OC and in 10 subjects not taking OC, so the true risk ratio was (20/10,000) / (10/10,000) = 2.
|
Unbiased Results |
Thromboembolism |
Non-diseased |
Totaal |
|---|---|---|---|
|
Oral Contraceptives |
20 |
9980 |
10,000 |
|
Unexposed |
10 |
9990 |
10,000 |
This unbiased data would give a risk ratio as follows:
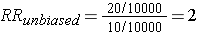
However, suppose there were substantial loses to follow-up in both groups, and a greater tendency to loose subjects taking oral contraceptives who developed thromboembolism. In other words, there was differential loss to follow up with loss of 12 diseased subjects in the group taking oral contraceptives, but loss of only 2 subjects with thromboembolism in the unexposed group. This might result in a contingency table like the one shown below.
|
Biased Results |
Thromboembolism |
Non-diseased |
Totaal |
|---|---|---|---|
|
Oral Contraceptives |
8 |
5980 |
5988 |
|
Unexposed |
8 |
5984 |
5992 |
This biased data would give a risk ratio as follows:
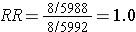
So, in this scenario both exposure groups lost about 40% of their subjects during the follow up period, but there was a greater loss of diseased subjects in the exposed group than in the unexposed group, and it was this differential loss to followup that biased the results.
|
Selection Bias |
Diseased |
Non-diseased |
|---|---|---|
|
Exposed |
|
|
|
Non-exposed |
|
|
Again, depending on which category is underreported as a result of differential loss to follow-up, either an underestimate or overestimate of effect (association) can occur.

The only way to prevent bias from loss to follow-up is to maintain high follow up rates (>80%). This can be achieved by:
The "health worker" effect is really a special type of selection bias that occurs in cohort studies of occupational exposures when the general population is used as the comparison group. The general population consists of both healthy people and unhealthy people. Those who are not healthy are less likely to be employed, while the employed work force tends to have fewer sick people. Moreover, people with severe illnesses would be most likely to be excluded from employment, but not from the general population. As a result, comparisons of mortality rates between an employed group and the general population will be biased.
Suppose, for example, that a given occupational exposure truly increases the risk of death by 20% (RR=1.2). Suppose also that the general population has an overall risk of death that is 10% higher than that of the employed workforce. Given this scenario, use of the general population as a comparison group would result in a underestimate of the risk ratio, i.e. RR=1.1.
Another possibility is that the exposure being tested is not associated with any difference in risk of death (i.e., true RR=1.0). If the general population is used as a comparison group the estimated RR might be around 0.9. Aschengrau and Seage cite a report (Link to report) that found a 16% lower mortality rate (standardized mortality rate = 0.84 in radiation-exposed workers at the Portsmouth Shipyard. It was noted, however, that the radiation workers had to undergo a special physical examination in order to be eligible to work in this particular program. Consequently, it is likely that their baseline health was significantly better than that of the population at large.
From the previous section it should be clear that, even if the categorization of subjects regarding exposure and outcome is perfectly accurate, bias can be introduced differential selection or retention in a study. The converse is also true: even if the selection and retention into the study is a fair representation of the population from which the samples were drawn, the estimate of association can be biased if subjects are incorrectly categorized with respect to their exposure status or outcome. These errors are often referred to as misclassification, and the mechanism that produces these errors can result in either non-differential or differential misclassification. Ken Rothman distinguishes these as follows:
"For exposure misclassification, the misclassification is nondifferential if it is unrelated to the occurrence or presence of disease; if the misclassification of exposure is different for those with and without disease, it is differential. Similarly, misclassification of disease [outcome] is nondifferential if it is unrelated to the exposure; otherwise, it is differential."
Nondifferential misclassification means that the frequency of errors is approximately the same in the groups being compared. Misclassification of exposure status is more of a problem than misclassification of outcome (as explained on page 6), but a study may be biased by misclassification of either exposure status, or outcome status, or both.
Nondifferential misclassification of a dichotomous exposure occurs when errors in classification occur to the same degree regardless of outcome. Nondifferential misclassification of exposure is a much more pervasive problem than differential misclassification (in which errors occur with greater frequency in one of the study groups). The figure below illustrates a hypothetical study in which all subjects are correctly classified with respect to outcome, but some of the exposed subjects in each outcome group were incorrectly classified as 'non-exposed.'
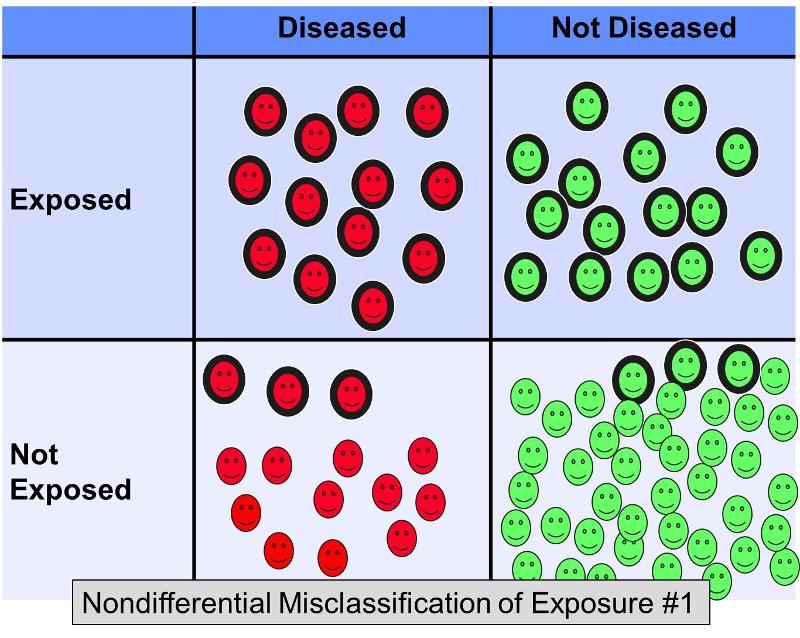
Suppose a case-control study was conducted to examine the association between a high fat diet and coronary artery disease. Subjects with heart disease and controls without heart disease might be recruited and asked to complete questionnaires about their dietary habits in order to categorize them as having diets with high fat content or not. It is difficult to assess dietary fat content accurately from questionnaires, so it would not be surprising if there were errors in classification of exposure. However, it is likely that in this scenario the misclassification would occur with more or less equal frequency regardless of the eventual disease status. Nondifferential misclassification of a dichotomous exposure always biases toward the null. In other words, if there is an association, it tends to minimize it regardless of whether it is a positive or a negative association.
The figure above depicts a scenario in which disease status is correctly classified, but some of the exposed subjects are incorrectly classified as non-exposed. This would result in bias toward the null. Rothman gives a hypothetical example in which the true odds ratio for the association between a high fat diet and coronary heart disease is 5.0, but if about 20% of the exposed subjects were misclassified as 'not exposed' in both disease groups, the biased estimate might give an odds ratio of, say, 2.4. In other words, it resulted in bias toward the null.
However, now consider what would happen in the same example if 20% of the exposed subjects were misclassified as 'not exposed' in both outcome groups, AND 20% of the non-exposed subjects were misclassified as 'exposed' in both groups - in other words a scenario that looked something like this:
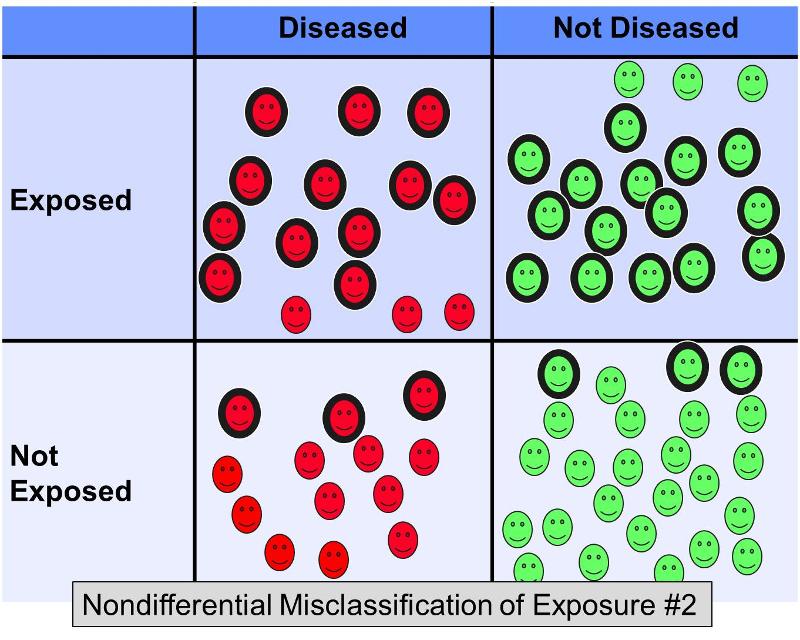
This additional nondifferential misclassification would result in even more severe bias toward the null, giving an odds ratio of perhaps 2.0.
Note that If there are multiple exposure categories, i.e. if the exposure is not dichotomous, then nondifferential misclassification may bias the estimate either toward the null or away from it, depending on the categories into which subjects are misclassified.
Mechanisms for Nondifferential Misclassification
Nondifferential misclassification can occur in a number of ways. Records may be incomplete, e.g., a medical record in which none of the healthcare workers remember to ask about tobacco use. There may be errors in recording or interpreting information in records, or there may be errors in assigning codes to disease diagnoses by clerical workers who are unfamiliar with a patient's hospital course, diagnosis, and treatment. Subjects completing questionnaires or being interviewed may have difficulty in remembering past exposures. Note that if difficulty in remembering past exposures occurs to the same extent in both groups being compared, then there is nondifferential misclassification, which will bias toward the null. However, if one outcome group in a case-control study remembers better than the other, then there is a differential misclassification which is called "recall bias." Recall bias is described below under differential misclassification of exposure.
If errors in classification of exposure status occur more frequently in one of the groups being compared, then differential misclassification will occur, and the estimate of association can be over estimated or under estimated. There are several mechanisms by which differential misclassification of exposure can occur.
Recall bias occurs when there are systematic differences in the way subjects remember or report exposures or outcomes. Recall bias can occur in either case-control studies or retrospective cohort studies. In a case-control study: subjects with disease may remember past exposures differently (more or less accurately) than those who do not have the disease.
Example:
Mothers of children with birth defects are likely to remember drugs they took during pregnancy differently than mothers of normal children. In this particular situation the bias is sometimes referred to as maternal recall bias. Mothers of the affected infants are likely to have thought about their drug use and other exposures during pregnancy to a much greater extent than the mothers of normal children. The primary difference arises more from under reporting of exposures in the control group rather than over reporting in the case group. However, it is also possible for the mothers in the case group to under report their past exposures. For example, mothers of infants who died from SIDS may be inclined to under report their use of alcohol or recreational drugs during pregnancy.
Recall bias occurs most often in case-control studies, but it can also occur in retrospective cohort studies. For example, those who have been exposed to a potentially harmful agent in the past may remember their subsequent outcomes with a different degree of completeness or accuracy.
Example:
In the retrospective portion of the Ranch Hand Study which looked at effects of exposure to Agent Orange (dioxin). Pilots who had been exposed may have had a greater tendency to remember skin rashes that occurred during the year following exposure.

Pitfall: In a case-control study, if both cases and controls have more or less equal difficulty in remembering past exposures accurately, it is nondifferential, and it is a form of nondifferential misclassification. In contrast, if one group remembers past exposures more accurately than the other, then it is called "recall bias" which is a differential type of misclassification.
Ways to Reduce Recall Bias
(Also Recorder Bias)
Differential bias can be introduced into a study when there are systematic differences in soliciting, recording, or interpreting information on exposure (in a case-control study) or outcome (in retrospective and prospective cohort studies and in intervention studies [clinical trials]). This type of bias can also occur when data is collected by review of medical records if the reviewer (abstractor) interprets or records information differently for one group or if the reviewer searches for information more diligently for one group. Since this is introduces a differential misclassification, it can cause bias either toward or away from the null, depending on the circumstances.
Ways to Reduce Interviewer Bias
Obviously, if the data for each of the groups being compared comes from different sources, the accuracy of the data may be better in one group, and this will introduce differential misclassification. For example, if exposure data for a case group were obtained from a facility specializing in the care of that condition and data from the comparison group were obtained from another source, there might be significant differences in the completeness and accuracy of the exposure data.
Misclassification of outcomes can also introduce bias into a study, but it usually has much less of an impact than misclassification of exposure. First, most of the problems with misclassification occur with respect to exposure status since exposures are frequently more difficult to assess and categorize. We glibly talk about smokers and non-smokers, but what do these terms really mean? One needs to consider how heavily the individual smoked, the duration, how long ago they started, whether and when they stopped, and even whether they inhaled or whether they were exposed to environmental smoke. In addition, as illustrated above, there are a number of mechanisms by which misclassification of exposure can be introduced. In contrast, most outcomes are more definitive and there are few mechanisms that introduce errors in outcome classification.
Another important consideration is that most of the outcomes that one studies are relatively uncommon; even when an association does exist, the majority of exposed and non-exposed subjects do not experience the outcome. As a result, there is much less potential for errors to have a major effect in distorting the measure of association.
Certainly there may be clerical and diagnostic errors in classification of outcome, but compared to the frequency of exposure misclassification, errors in outcome classification tend to be less common and have much less impact on the estimate of association. In addition to having little impact on the estimate of effect, misclassification of outcome will generally bias toward the null, so if an association is demonstrated, if anything the true effect might be slightly greater.
Example:
Consider the case-control conducted by Doll and Hill in 1947. This was one of the first analytic studies that examined the association between smoking and lung cancer. The study gathered data from more than twenty hospitals in the London area. Cases with a recent diagnosis of lung cancer were identified and interviewed about their past exposures, including a detailed history of smoking tobacco. Non-cancer control patients in the same hospitals were also interviewed. The study was quite extensive, but the bottom line was that statistically significant associations between smoking and lung cancer were found in both males and females (although the association was not as strong in females.
The investigators took steps to verify the diagnoses whenever possible by checking operative findings, pathology reports, and autopsy findings. Given the nature of the disease and the efforts to verify the diagnosis, it is likely that the diagnosis was correct in the vast majority of subjects. However, far more problematic was the classification of the degree of exposure to tobacco. The assessment of exposure could be influenced not only by misclassification as a result of trying to remember the details of smoking exposure over a lifetime, but the potential problems with recall bias and interviewer bias.
To illustrate differential misclassification of outcome Rothman uses the following example"
"Suppose a follow-up study were undertaken to compare incidence rates of emphysema among smokers and nonsmokers. Emphysema is a disease that may go undiagnosed without unusual medical attention. If smokers, because of concern about health effects of smoking (such as bronchitis), seek medical attention to a greater degree than nonsmokers, then emphysema might be diagnosed more frequently among smokers than among nonsmokers simply as a consequence of the greater medical attention. Unless steps were taken to ensure comparable follow-up, an information bias would result. An 'excess' of emphysema incidence would be found among smokers compared with nonsmokers that is unrelated to any biologic effect of smoking. This is an example of differential misclassification, since the underdiagnosis of emphysema, a misclassification error, occurs more frequently for nonsmokers than for smokers."
Non-differential misclassification of a dichotomous outcome will generally bias toward the null, but there are situations in which it will not bias the risk ratio. Bias in the risk difference depends upon the sensitivity (probability that someone who truly has the outcome will be identified as such) and specificity (probability that someone who does not have the outcome will be identified as such).
OPTIONAL
This is additional detail on the effects of non-differential misclassification of outcome that is not required in the introductory course, although it is required in Intermediate Epidemiology.
From "Modern Epidemiology" (3rd edition, page 142):
"Consider a cohort study in which 40 cases actually occur among 100 exposed subjects and 20 cases actually occur among 200 unexposed subjects. Then, the actual risk ratio is (40/100)/(20/200) = 4, and the actual risk difference is 40/100-20/200 = 0.30. Suppose that specificity of disease detection is perfect (there are no false positives), but sensitivity is only 70% in both exposure groups. (that is sensitivity of disease detection is nondifferential and does not depend on errors in classification of exposure). The expected numbers detected will then be 0.70(40) = 28 exposed cases and 0.70(20) = 14 unexposed cases, which yield an expected risk-ratio estimate of (28/100)/(14/200) = 4 and expected risk-difference estimate of 28/100 - 14/200 = 0.21. Thus, the disease misclassification produced no bias in the risk ratio, but the expected risk-difference estimate is only 0.21/0.30 = 70% of the actual risk difference.
"This example illustrates how independent nondifferential disease misclassification with perfect specificity will not bias the risk-ratio estimate, but will downwardly bias the absolute magnitude of the risk-difference estimate by a factor equal to the false-negative probability (Rogers and MacMahon, 1995). With this type of misclassification, the odds ratio and the rate ratio will remain biased toward the null, although the bias will be small when the risk of disease is low (<10%) in both exposure groups. This approximation is a consequence of the relation of the odds ratio and the rate ratio to the risk ratio when the disease risk is low in all exposure groups."
The scenario described above could be summarized with the following contingency tables.
First, consider the true relationship:
Table - True Relationship A:
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
40 |
60 |
100 |
|
Unexposed |
20 |
180 |
200 |
Sensitivity = 100% (all disease cases were detected)
Specificity = 100% (all non-cases correctly classified)
Risk Ratio = (40/100)/(20/200) = 4
Risk Difference = 40/100-20/200 = 0.30
Then consider:
Table - Misclassification of Outcome #1
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
28 |
72 |
100 |
|
Unexposed |
14 |
186 |
200 |
Sensitivity = 70% (30% false negative rate)
Specificity = 100% (all non-cases correctly classified)
Risk Ratio = (28/100)/(14/200) = 4
Risk Difference = 28/100-14/200 = 0.21
This illustrates the effect when all of the non-diseased subjects are correctly classified, but some of the diseased subjects are misclassified as non-diseased. As you can see the risk ratio is not biased under these circumstances, but the risk difference is. The reason for this is that decreased sensitivity results in a proportionate decrease in the cumulative incidence in both groups, so the ratio of the two (the risk ratio) is unchanged. However, the groups are of unequal size, so the absolute difference between the groups (the risk difference) does change.
It is also possible for non-diseased subjects to be incorrectly classified as diseased, i.e., specificity <100%. For the scenario above, suppose that sensitivity had been 100% (all of the truly diseased subjects were identified), but the specificity was only 70%, i.e., 70% of the non-diseased people were correctly categorized as non-diseased, but 30% of them were incorrectly identified as diseased. In that case the scenario would give a contingency table as illustrated below.
Table - Misclassification of Outcome #2
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
58 |
42 |
100 |
|
Unexposed |
74 |
126 |
200 |
Sensitivity = 100% (all disease cases were detected)
Specificity = 70% (30% of non-cases incorrectly classified)
Risk Ratio = (58/100)/(74/200) = 1.57
Risk Difference = 58/100-74/200 = 0.58-0.37= 0.21
Here, the specificity is 70% in both groups, but there are more non-diseased subjects in the unexposed, so the result is a disproportionate increase in the apparent number of diseased subjects in the unexposed group, and both the risk ratio and the risk difference are underestimated.
This is also true when the number of subjects in the exposed group is larger as illustrated in the example below.
First, consider true relationship B:
Table - True Relationship B
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
40 |
160 |
200 |
|
Unexposed |
10 |
90 |
100 |
Sensitivity = 100% (all disease cases were detected)
Specificity = 100% (all non-cases correctly classified)
Risk Ratio = (40/200)/(10/100) = 0.2/0.1 = 2
Risk Difference = 40/200-10/100 = 0.20-0.10 = 0.21
In contrast, consider the next table with misclassification of outcome, but a larger number of exposed subjects..
Table - Misclassification of Outcome #3
|
|
Diseased |
Non-diseased |
Total |
|---|---|---|---|
|
Exposed |
88 |
112 |
200 |
|
Unexposed |
37 |
63 |
100 |
Sensitivity = 100% (all disease cases were detected)
Specificity = 70% (30% of non-cases incorrectly classified)
Risk Ratio = (88/200)/(40/100) = 0.44/0.40 = 1.1
Risk Difference = 88/200-40/100 = 0.44-0.40= 0.04
In this example, sensitivity is again 100% and specificity is 70%. As a result, 0.30*160 = 48 diseased subjects in the exposed group are incorrectly classified as diseased and move from cell B to cell A. Similarly, in the unexposed group, 0.30*90 = 27 non-diseased people are incorrectly classified as diseased and move from cell D to cell C. Again, the risk ratio and the risk difference are biased toward the null.
When listening to a presentation or reading an article in which data is presented to support a conclusion, one must always consider alternative explanations that may threaten the validity of the conclusions. Specifically, one needs to consider whether random error, bias or confounding could have undermined the conclusions to a significant extent. Virtually all studies have potential flaws, but carefully done studies are designed and conducted in a way that minimizes these problems so that they don't have any important effect on the conclusions. However, in other studies that are conducted in difficult circumstances (e.g., a prospective cohort study in a homeless population in which one would expect difficulty maintaining follow-up) or in poorly designed studies, biases may have a major impact and produce large overestimates or underestimates of the true association. In view of this, it is always important to ask oneself:
Direction of Bias
 Developing skill in identifying bias and predicting its potential impact on an association requires practice and experience. Here is a series of questions on bias from old exams that will give you some practice and sharpen your understanding of bias.
Developing skill in identifying bias and predicting its potential impact on an association requires practice and experience. Here is a series of questions on bias from old exams that will give you some practice and sharpen your understanding of bias.
The Doll and Hill Case-Control Study
Read the summary in the iframe below (a summary of the classic case-control study by Sir Richard Doll and Bradford Hill in 1948), and then answer the questions beneath the frame.





The next iFrame is a PDF summary of a study by Joann Manson and others looking at the effect of ecercise on coronary heart disease in women. Read the summary and then answer the questions beneath the iFrame.
Manson et al.: The Effect of Exercise on Coronary Heart Disease in Women


