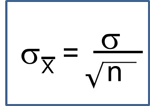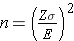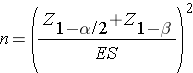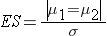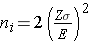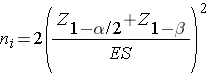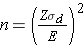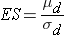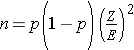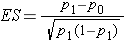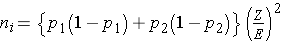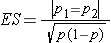Summary
Determining the appropriate design of a study is more important than the statistical analysis; a poorly designed study can never be salvaged, whereas a poorly analyzed study can be re-analyzed. A critical component in study design is the determination of the appropriate sample size. The sample size must be large enough to adequately answer the research question, yet not too large so as to involve too many patients when fewer would have sufficed. The determination of the appropriate sample size involves statistical criteria as well as clinical or practical considerations. Sample size determination involves teamwork; biostatisticians must work closely with clinical investigators to determine the sample size that will address the research question of interest with adequate precision or power to produce results that are clinically meaningful.
The following table summarizes the sample size formulas for each scenario described here. The formulas are organized by the proposed analysis, a confidence interval estimate or a test of hypothesis.
|
Situation |
Sample Size to Estimate Confidence Interval |
Sample Size to Conduct Test of Hypothesis |
|---|---|---|
|
Continuous Outcome, One Sample: CI for μ, H0: μ = μ0 |
|
|
|
Continuous Outcome, Two Independent Samples: CI for ( μ1-μ2), H0: μ1 = μ2 |
|
|
|
Continuous Outcome, Two Matched Samples: CI for μd , H0: μd = 0 |
|
|
|
Dichotomous Outcome, One Sample: CI for p , H0: p = p0 |
|
|
|
Dichotomous Outcome, Two Independent Samples: CI for (p1-p2) , H0: p1 = p2 |
|
|