
Correlation and Linear Regression
Author:
Lisa Sullivan, PhD
Professor of Biostatistics
Boston University School of Public Health

In this section we discuss correlation analysis which is a technique used to quantify the associations between two continuous variables. For example, we might want to quantify the association between body mass index and systolic blood pressure, or between hours of exercise per week and percent body fat. Regression analysis is a related technique to assess the relationship between an outcome variable and one or more risk factors or confounding variables (confounding is discussed later). The outcome variable is also called the response or dependent variable, and the risk factors and confounders are called the predictors, or explanatory or independent variables. In regression analysis, the dependent variable is denoted "Y" and the independent variables are denoted by "X".
[ NOTE: The term "predictor" can be misleading if it is interpreted as the ability to predict even beyond the limits of the data. Also, the term "explanatory variable" might give an impression of a causal effect in a situation in which inferences should be limited to identifying associations. The terms "independent" and "dependent" variable are less subject to these interpretations as they do not strongly imply cause and effect.
After completing this module, the student will be able to:

In correlation analysis, we estimate a sample correlation coefficient, more specifically the Pearson Product Moment correlation coefficient. The sample correlation coefficient, denoted r,
ranges between -1 and +1 and quantifies the direction and strength of the linear association between the two variables. The correlation between two variables can be positive (i.e., higher levels of one variable are associated with higher levels of the other) or negative (i.e., higher levels of one variable are associated with lower levels of the other).
The sign of the correlation coefficient indicates the direction of the association. The magnitude of the correlation coefficient indicates the strength of the association.
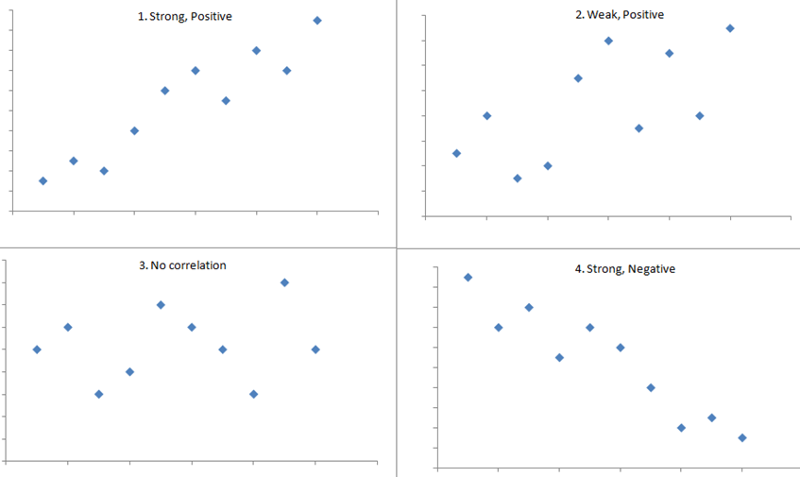
For example, a correlation of r = 0.9 suggests a strong, positive association between two variables, whereas a correlation of r = -0.2 suggest a weak, negative association. A correlation close to zero suggests no linear association between two continuous variables.
It is important to note that there may be a non-linear association between two continuous variables, but computation of a correlation coefficient does not detect this. Therefore, it is always important to evaluate the data carefully before computing a correlation coefficient. Graphical displays are particularly useful to explore associations between variables.
The figure below shows four hypothetical scenarios in which one continuous variable is plotted along the X-axis and the other along the Y-axis.


A small study is conducted involving 17 infants to investigate the association between gestational age at birth, measured in weeks, and birth weight, measured in grams.
|
Infant ID # |
Gestational Age (weeks) |
Birth Weight (grams) |
|---|---|---|
|
1 |
34.7 |
1895 |
|
2 |
36.0 |
2030 |
|
3 |
29.3 |
1440 |
|
4 |
40.1 |
2835 |
|
5 |
35.7 |
3090 |
|
6 |
42.4 |
3827 |
|
7 |
40.3 |
3260 |
|
8 |
37.3 |
2690 |
|
9 |
40.9 |
3285 |
|
10 |
38.3 |
2920 |
|
11 |
38.5 |
3430 |
|
12 |
41.4 |
3657 |
|
13 |
39.7 |
3685 |
|
14 |
39.7 |
3345 |
|
15 |
41.1 |
3260 |
|
16 |
38.0 |
2680 |
|
17 |
38.7 |
2005 |
We wish to estimate the association between gestational age and infant birth weight. In this example, birth weight is the dependent variable and gestational age is the independent variable. Thus y=birth weight and x=gestational age. The data are displayed in a scatter diagram in the figure below.
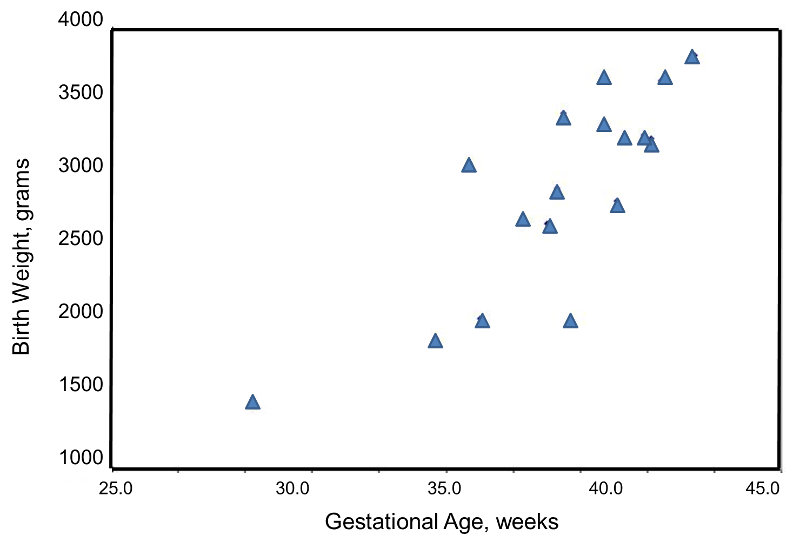
Each point represents an (x,y) pair (in this case the gestational age, measured in weeks, and the birth weight, measured in grams). Note that the independent variable, gestational age) is on the horizontal axis (or X-axis), and the dependent variable (birth weight) is on the vertical axis (or Y-axis). The scatter plot shows a positive or direct association between gestational age and birth weight. Infants with shorter gestational ages are more likely to be born with lower weights and infants with longer gestational ages are more likely to be born with higher weights.
The formula for the sample correlation coefficient is:
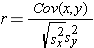
where Cov(x,y) is the covariance of x and y defined as
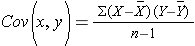
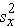 and
and 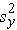 are the sample variances of x and y, defined as follows:
are the sample variances of x and y, defined as follows:
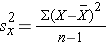 and
and 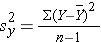
The variances of x and y measure the variability of the x scores and y scores around their respective sample means of X and Y considered separately. The covariance measures the variability of the (x,y) pairs around the mean of x and mean of y, considered simultaneously.


To compute the sample correlation coefficient, we need to compute the variance of gestational age, the variance of birth weight, and also the covariance of gestational age and birth weight.
We first summarize the gestational age data. The mean gestational age is:
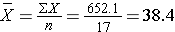
To compute the variance of gestational age, we need to sum the squared deviations (or differences) between each observed gestational age and the mean gestational age. The computations are summarized below.
|
Infant ID # |
Gestational Age (weeks) |
|
|
|---|---|---|---|
|
1 |
34.7 |
-3.7 |
13.69 |
|
2 |
36.0 |
-2.4 |
5.76 |
|
3 |
29.3 |
-9.1 |
82,81 |
|
4 |
40.1 |
1.7 |
2.89 |
|
5 |
35.7 |
-2.7 |
7.29 |
|
6 |
42.4 |
4.0 |
16.0 |
|
7 |
40.3 |
1.9 |
3.61 |
|
8 |
37.3 |
-1.1 |
1.21 |
|
9 |
40.9 |
2.5 |
6.25 |
|
10 |
38.3 |
-0.1 |
0.01 |
|
11 |
38.5 |
0.1 |
0.01 |
|
12 |
41.4 |
3.0 |
9.0 |
|
13 |
39.7 |
1.3 |
1.69 |
|
14 |
39.7 |
1.3 |
1.69 |
|
15 |
41.1 |
2.7 |
7.29 |
|
16 |
38.0 |
-0.4 |
0.16 |
|
17 |
38.7 |
0.3 |
0.09 |
|
|
|
|
|
The variance of gestational age is:
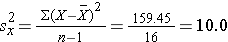
Next, we summarize the birth weight data. The mean birth weight is:
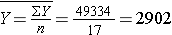
The variance of birth weight is computed just as we did for gestational age as shown in the table below.
|
Infant ID# |
Birth Weight |
|
|
|---|---|---|---|
|
1 |
1895 |
-1007 |
1,014,049 |
|
2 |
2030 |
-872 |
760,384 |
|
3 |
1440 |
-1462 |
2,137,444 |
|
4 |
2835 |
-67 |
4,489 |
|
5 |
3090 |
188 |
35,344 |
|
6 |
3827 |
925 |
855,625 |
|
7 |
3260 |
358 |
128,164 |
|
8 |
2690 |
-212 |
44,944 |
|
9 |
3285 |
383 |
146,689 |
|
10 |
2920 |
18 |
324 |
|
11 |
3430 |
528 |
278,764 |
|
12 |
3657 |
755 |
570,025 |
|
13 |
3685 |
783 |
613,089 |
|
14 |
3345 |
443 |
196,249 |
|
15 |
3260 |
358 |
128,164 |
|
16 |
2680 |
-222 |
49,284 |
|
17 |
2005 |
-897 |
804,609 |
|
|
|
|
|
The variance of birth weight is:
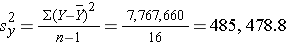
Next we compute the covariance:
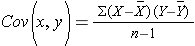
To compute the covariance of gestational age and birth weight, we need to multiply the deviation from the mean gestational age by the deviation from the mean birth weight for each participant, that is:
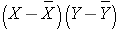
The computations are summarized below. Notice that we simply copy the deviations from the mean gestational age and birth weight from the two tables above into the table below and multiply.
|
Infant ID# |
|
|
|
|---|---|---|---|
|
1 |
-3.7 |
-1007 |
3725.9 |
|
2 |
-2.4 |
-872 |
2092.8 |
|
3 |
-9,1 |
-1462 |
13,304.2 |
|
4 |
1.7 |
-67 |
-113.9 |
|
5 |
-2.7 |
188 |
-507.6 |
|
6 |
4.0 |
925 |
3700.0 |
|
7 |
1.9 |
358 |
680.2 |
|
8 |
-1.1 |
-212 |
233.2 |
|
9 |
2.5 |
383 |
957.5 |
|
10 |
-0.1 |
18 |
-1.8 |
|
11 |
0.1 |
528 |
52.8 |
|
12 |
3.0 |
755 |
2265.0 |
|
13 |
1.3 |
783 |
1017.9 |
|
14 |
1.3 |
443 |
575.9 |
|
15 |
2.7 |
358 |
966.6 |
|
16 |
-0.4 |
-222 |
88.8 |
|
17 |
0.3 |
-897 |
-269.1 |
|
Total = 28,768.4 |
The covariance of gestational age and birth weight is:
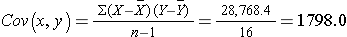
Finally, we can ow compute the sample correlation coefficient:
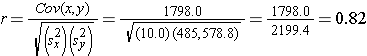
Not surprisingly, the sample correlation coefficient indicates a strong positive correlation.
As we noted, sample correlation coefficients range from -1 to +1. In practice, meaningful correlations (i.e., correlations that are clinically or practically important) can be as small as 0.4 (or -0.4) for positive (or negative) associations. There are also statistical tests to determine whether an observed correlation is statistically significant or not (i.e., statistically significantly different from zero). Procedures to test whether an observed sample correlation is suggestive of a statistically significant correlation are described in detail in Kleinbaum, Kupper and Muller.1
Regression analysis is a widely used technique which is useful for many applications. We introduce the technique here and expand on its uses in subsequent modules.
Simple linear regression is a technique that is appropriate to understand the association between one independent (or predictor) variable and one continuous dependent (or outcome) variable. For example, suppose we want to assess the association between total cholesterol (in milligrams per deciliter, mg/dL) and body mass index (BMI, measured as the ratio of weight in kilograms to height in meters2) where total cholesterol is the dependent variable, and BMI is the independent variable. In regression analysis, the dependent variable is denoted Y and the independent variable is denoted X. So, in this case, Y=total cholesterol and X=BMI.
When there is a single continuous dependent variable and a single independent variable, the analysis is called a simple linear regression analysis . This analysis assumes that there is a linear association between the two variables. (If a different relationship is hypothesized, such as a curvilinear or exponential relationship, alternative regression analyses are performed.)
The figure below is a scatter diagram illustrating the relationship between BMI and total cholesterol. Each point represents the observed (x, y) pair, in this case, BMI and the corresponding total cholesterol measured in each participant. Note that the independent variable (BMI) is on the horizontal axis and the dependent variable (Total Serum Cholesterol) on the vertical axis.
BMI and Total Cholesterol
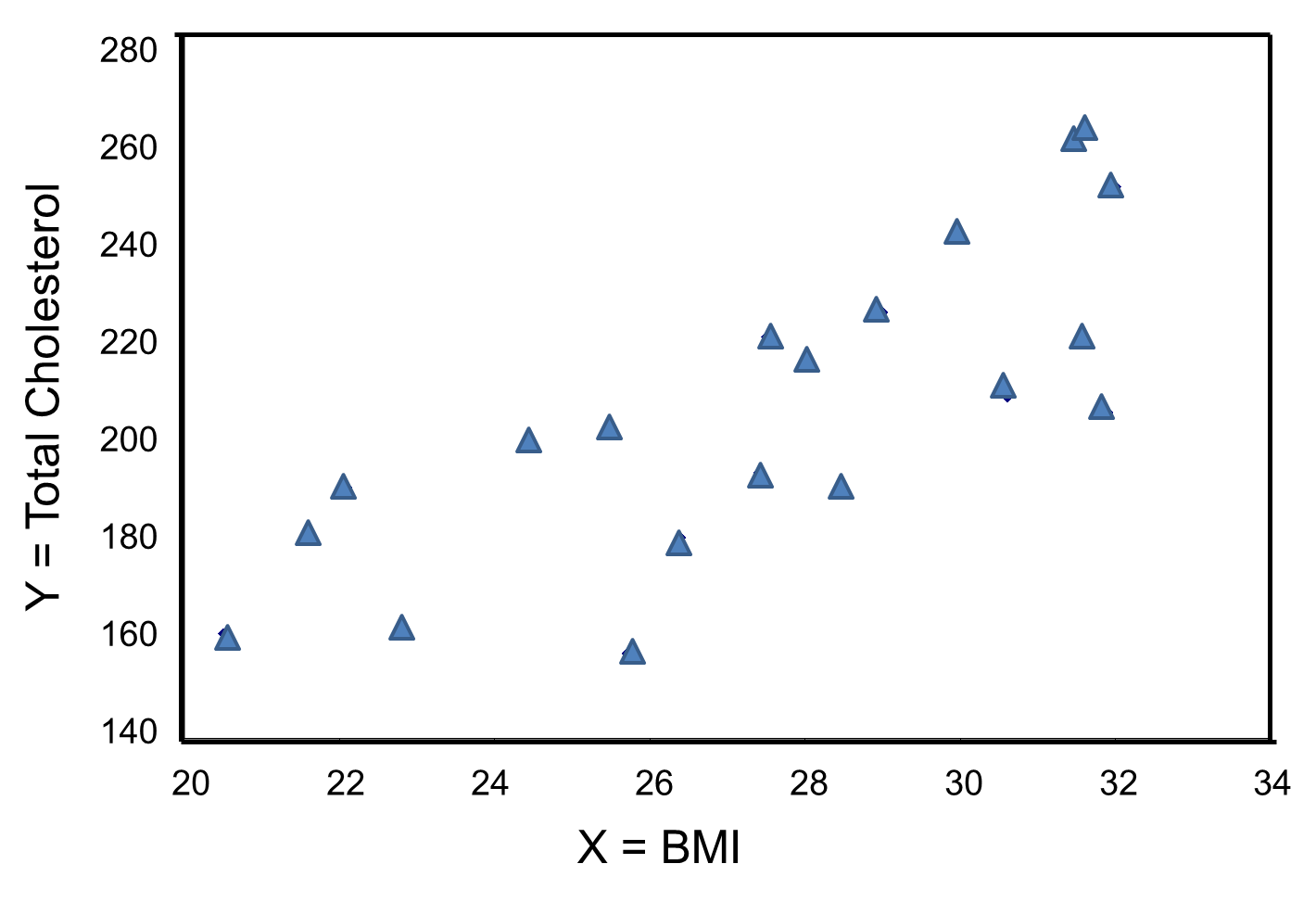
The graph shows that there is a positive or direct association between BMI and total cholesterol; participants with lower BMI are more likely to have lower total cholesterol levels and participants with higher BMI are more likely to have higher total cholesterol levels. In contrast, suppose we examine the association between BMI and HDL cholesterol.
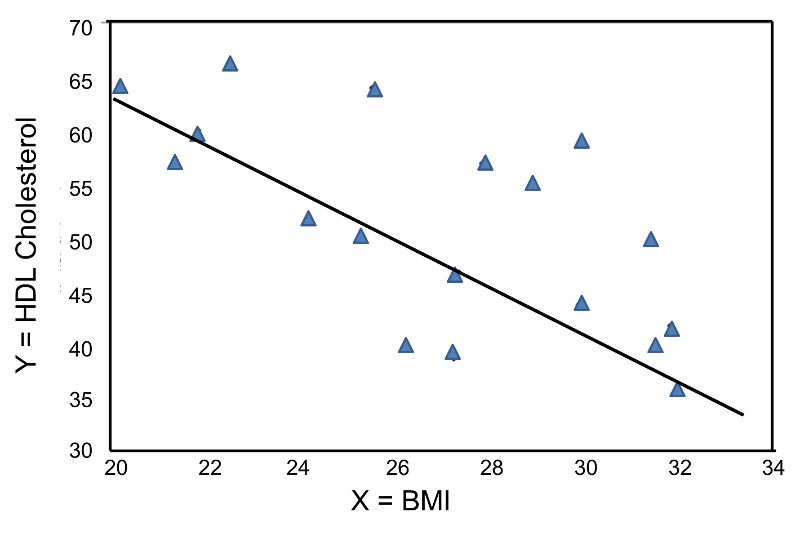
In contrast, the graph below depicts the relationship between BMI and HDL cholesterol in the same sample of n=20 participants.
BMI and HDL Cholesterol
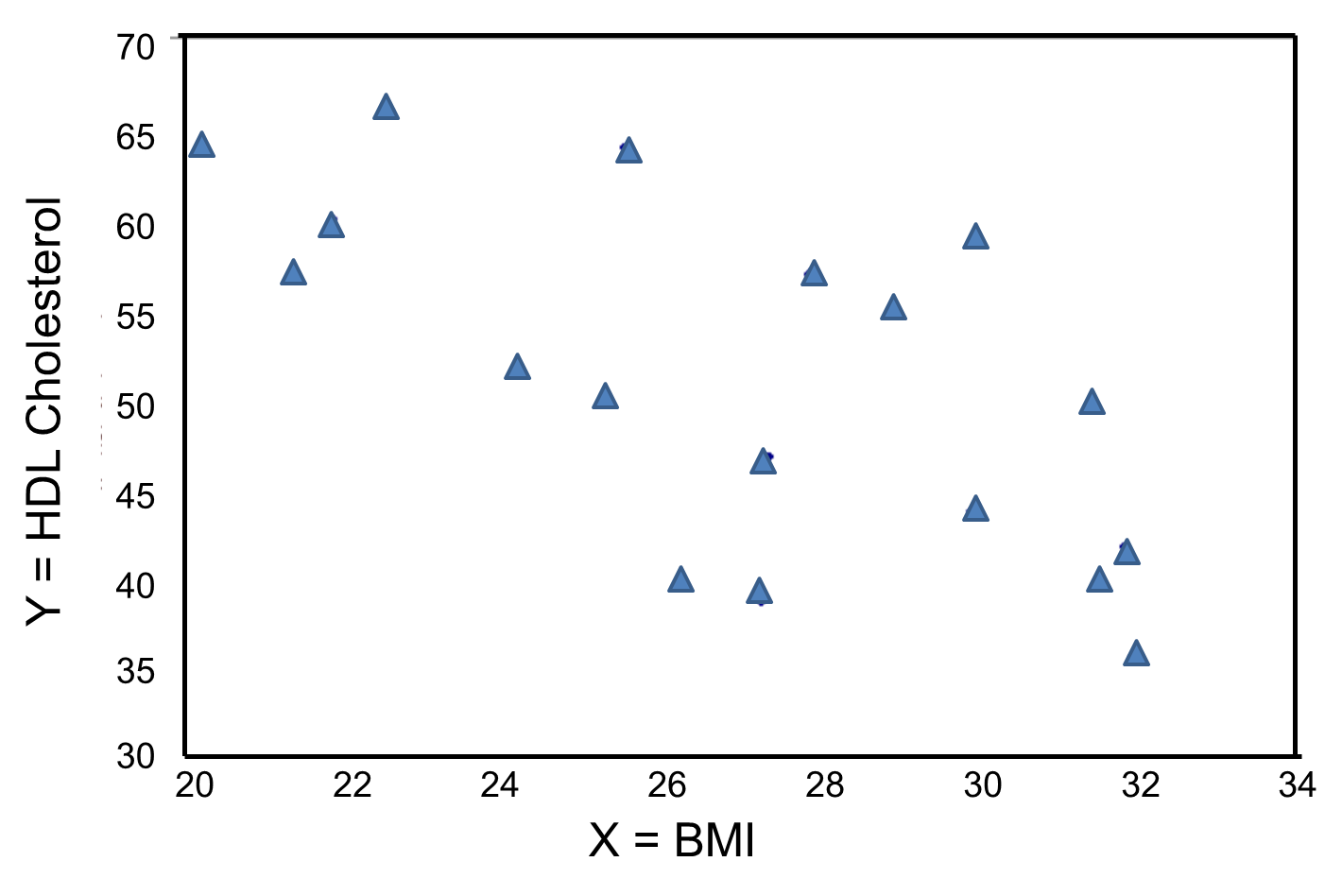
This graph shows a negative or inverse association between BMI and HDL cholesterol, i.e., those with lower BMI are more likely to have higher HDL cholesterol levels and those with higher BMI are more likely to have lower HDL cholesterol levels.
For either of these relationships we could use simple linear regression analysis to estimate the equation of the line that best describes the association between the independent variable and the dependent variable. The simple linear regression equation is as follows:
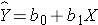
where Y is the predicted or expected value of the outcome, X is the predictor, b0 is the estimated Y-intercept, and b1 is the estimated slope. The Y-intercept and slope are estimated from the sample data, and they are the values that minimize the sum of the squared differences between the observed and the predicted values of the outcome, i.e., the estimates minimize:
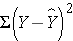
These differences between observed and predicted values of the outcome are called residuals. The estimates of the Y-intercept and slope minimize the sum of the squared residuals, and are called the least squares estimates.1
|
Residuals Conceptually, if the values of X provided a perfect prediction of Y then the sum of the squared differences between observed and predicted values of Y would be 0. That would mean that variability in Y could be completely explained by differences in X. However, if the differences between observed and predicted values are not 0, then we are unable to entirely account for differences in Y based on X, then there are residual errors in the prediction. The residual error could result from inaccurate measurements of X or Y, or there could be other variables besides X that affect the value of Y.
|
Based on the observed data, the best estimate of a linear relationship will be obtained from an equation for the line that minimizes the differences between observed and predicted values of the outcome. The Y-intercept of this line is the value of the dependent variable (Y) when the independent variable (X) is zero. The slope of the line is the change in the dependent variable (Y) relative to a one unit change in the independent variable (X). The least squares estimates of the y-intercept and slope are computed as follows:
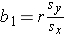
and
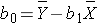
where
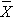 and
and 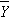
The least squares estimates of the regression coefficients, b 0 and b1, describing the relationship between BMI and total cholesterol are b0 = 28.07 and b1=6.49. These are computed as follows:
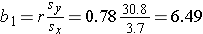
and
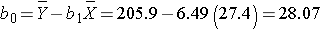
The estimate of the Y-intercept (b0 = 28.07) represents the estimated total cholesterol level when BMI is zero. Because a BMI of zero is meaningless, the Y-intercept is not informative. The estimate of the slope (b1 = 6.49) represents the change in total cholesterol relative to a one unit change in BMI. For example, if we compare two participants whose BMIs differ by 1 unit, we would expect their total cholesterols to differ by approximately 6.49 units (with the person with the higher BMI having the higher total cholesterol).
The equation of the regression line is as follows:
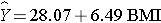
The graph below shows the estimated regression line superimposed on the scatter diagram.
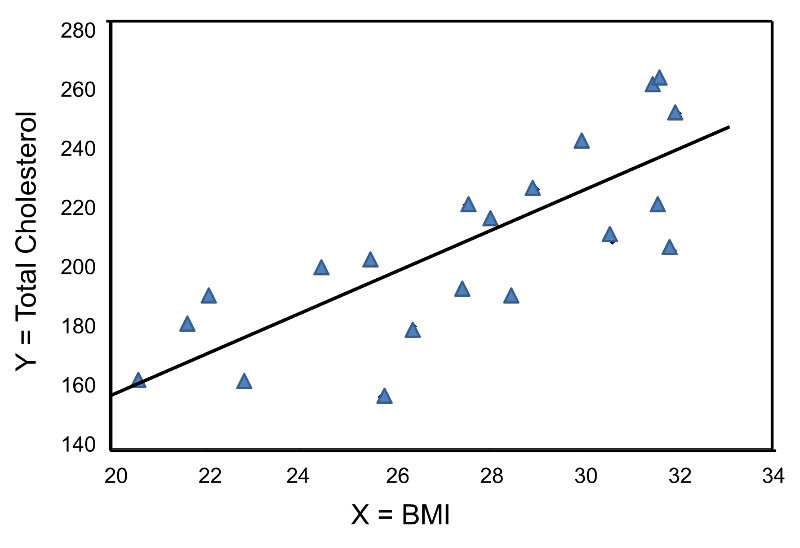
The regression equation can be used to estimate a participant's total cholesterol as a function of his/her BMI. For example, suppose a participant has a BMI of 25. We would estimate their total cholesterol to be 28.07 + 6.49(25) = 190.32. The equation can also be used to estimate total cholesterol for other values of BMI. However, the equation should only be used to estimate cholesterol levels for persons whose BMIs are in the range of the data used to generate the regression equation. In our sample, BMI ranges from 20 to 32, thus the equation should only be used to generate estimates of total cholesterol for persons with BMI in that range.
There are statistical tests that can be performed to assess whether the estimated regression coefficients (b0 and b1) are statistically significantly different from zero. The test of most interest is usually H0: b1=0 versus H1: b1≠0, where b1 is the population slope. If the population slope is significantly different from zero, we conclude that there is a statistically significant association between the independent and dependent variables.
The least squares estimates of the regression coefficients, b0 and b1, describing the relationship between BMI and HDL cholesterol are as follows: b0 = 111.77 and b1 = -2.35. These are computed as follows:
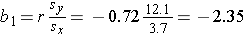
and
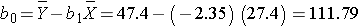
Again, the Y-intercept in uninformative because a BMI of zero is meaningless. The estimate of the slope (b1 = -2.35) represents the change in HDL cholesterol relative to a one unit change in BMI. If we compare two participants whose BMIs differ by 1 unit, we would expect their HDL cholesterols to differ by approximately 2.35 units (with the person with the higher BMI having the lower HDL cholesterol. The figure below shows the regression line superimposed on the scatter diagram for BMI and HDL cholesterol.
Linear regression analysis rests on the assumption that the dependent variable is continuous and that the distribution of the dependent variable (Y) at each value of the independent variable (X) is approximately normally distributed. Note, however, that the independent variable can be continuous (e.g., BMI) or can be dichotomous (see below).
Consider a clinical trial to evaluate the efficacy of a new drug to increase HDL cholesterol. We could compare the mean HDL levels between treatment groups statistically using a two independent samples t test. Here we consider an alternate approach. Summary data for the trial are shown below:
|
|
Sample Size |
Mean HDL |
Standard Deviation of HDL |
|---|---|---|---|
|
New Drug |
50 |
40.16 |
4.46 |
|
Placebo |
50 |
39.21 |
3.91 |
HDL cholesterol is the continuous dependent variable and treatment assignment (new drug versus placebo) is the independent variable. Suppose the data on n=100 participants are entered into a statistical computing package. The outcome (Y) is HDL cholesterol in mg/dL and the independent variable (X) is treatment assignment. For this analysis, X is coded as 1 for participants who received the new drug and as 0 for participants who received the placebo. A simple linear regression equation is estimated as follows:
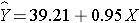
where Y is the estimated HDL level and X is a dichotomous variable (also called an indicator variable, in this case indicating whether the participant was assigned to the new drug or to placebo). The estimate of the Y-intercept is b0=39.21. The Y-intercept is the value of Y (HDL cholesterol) when X is zero. In this example, X=0 indicates assignment to the placebo group. Thus, the Y-intercept is exactly equal to the mean HDL level in the placebo group. The slope is estimated as b1=0.95. The slope represents the estimated change in Y (HDL cholesterol) relative to a one unit change in X. A one unit change in X represents a difference in treatment assignment (placebo versus new drug). The slope represents the difference in mean HDL levels between the treatment groups. Thus, the mean HDL for participants receiving the new drug is:
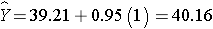
 -----
-----

A study was conducted to assess the association between a person's intelligence and the size of their brain. Participants completed a standardized IQ test and researchers used Magnetic Resonance Imaging (MRI) to determine brain size. Demographic information, including the patient's gender, was also recorded.

There is convincing evidence that active smoking is a cause of lung cancer and heart disease. Many studies done in a wide variety of circumstances have consistently demonstrated a strong association and also indicate that the risk of lung cancer and cardiovascular disease (i.e.., heart attacks) increases in a dose-related way. These studies have led to the conclusion that active smoking is causally related to lung cancer and cardiovascular disease. Studies in active smokers have had the advantage that the lifetime exposure to tobacco smoke can be quantified with reasonable accuracy, since the unit dose is consistent (one cigarette) and the habitual nature of tobacco smoking makes it possible for most smokers to provide a reasonable estimate of their total lifetime exposure quantified in terms of cigarettes per day or packs per day. Frequently, average daily exposure (cigarettes or packs) is combined with duration of use in years in order to quantify exposure as "pack-years".
It has been much more difficult to establish whether environmental tobacco smoke (ETS) exposure is causally related to chronic diseases like heart disease and lung cancer, because the total lifetime exposure dosage is lower, and it is much more difficult to accurately estimate total lifetime exposure. In addition, quantifying these risks is also complicated because of confounding factors. For example, ETS exposure is usually classified based on parental or spousal smoking, but these studies are unable to quantify other environmental exposures to tobacco smoke, and inability to quantify and adjust for other environmental exposures such as air pollution makes it difficult to demonstrate an association even if one existed. As a result, there continues to be controversy over the risk imposed by environmental tobacco smoke (ETS). Some have gone so far as to claim that even very brief exposure to ETS can cause a myocardial infarction (heart attack), but a very large prospective cohort study by Enstrom and Kabat was unable to demonstrate significant associations between exposure to spousal ETS and coronary heart disease, chronic obstructive pulmonary disease, or lung cancer. (It should be noted, however, that the report by Enstrom and Kabat has been widely criticized for methodological problems, and these authors also had financial ties to the tobacco industry.)
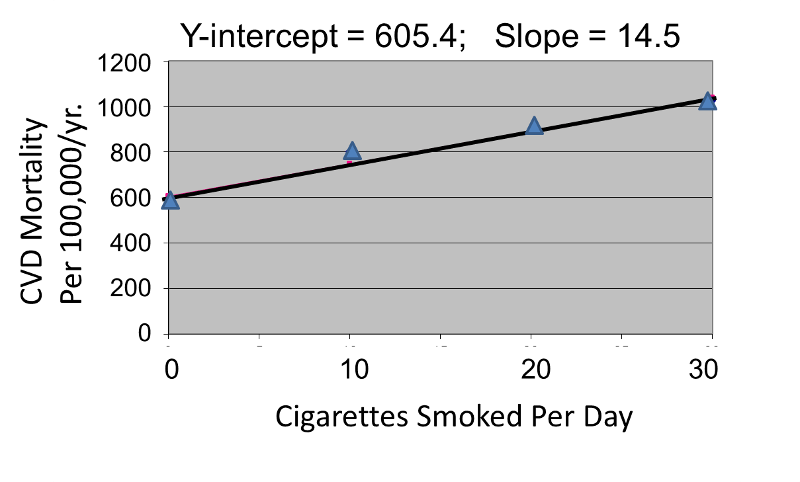
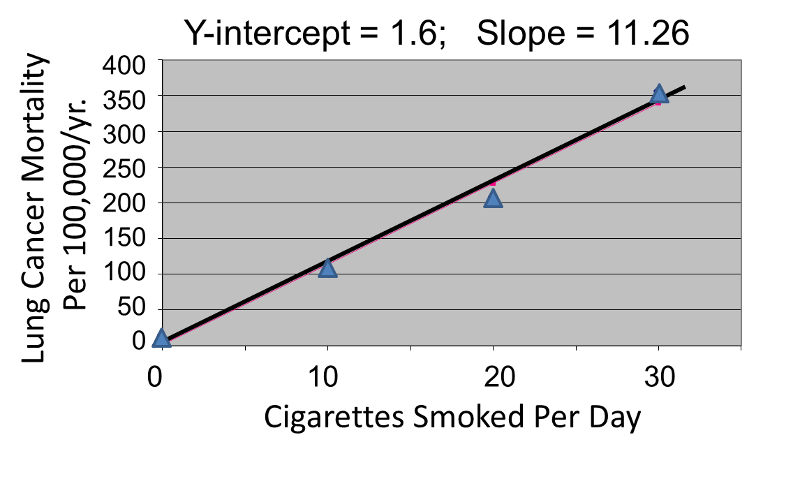
Correlation analysis provides a useful tool for thinking about this controversy. Consider data from the British Doctors Cohort. They reported the annual mortality for a variety of disease at four levels of cigarette smoking per day: Never smoked, 1-14/day, 15-24/day, and 25+/day. In order to perform a correlation analysis, I rounded the exposure levels to 0, 10, 20, and 30 respectively.
|
Cigarettes Smoked Per Day |
CVD Mortality Per 100,000 Men Per Year |
Lung Cancer Mortality Per 100,000 Men Per Year |
|---|---|---|
|
0 |
572 |
14 |
|
10 (actually 1-14) |
802 |
105 |
|
20 (actually 15-24) |
892 |
208 |
|
30 (actually >24) |
1025 |
355 |
The figures below show the two estimated regression lines superimposed on the scatter diagram. The correlation with amount of smoking was strong for both CVD mortality (r= 0.98) and for lung cancer (r = 0.99). Note also that the Y-intercept is a meaningful number here; it represents the predicted annual death rate from these disease in individuals who never smoked. The Y-intercept for prediction of CVD is slightly higher than the observed rate in never smokers, while the Y-intercept for lung cancer is lower than the observed rate in never smokers.
The linearity of these relationships suggests that there is an incremental risk with each additional cigarette smoked per day, and the additional risk is estimated by the slopes. This perhaps helps us think about the consequences of ETS exposure. For example, the risk of lung cancer in never smokers is quite low, but there is a finite risk; various reports suggest a risk of 10-15 lung cancers/100,000 per year. If an individual who never smoked actively was exposed to the equivalent of one cigarette's smoke in the form of ETS, then the regression suggests that their risk would increase by 11.26 lung cancer deaths per 100,000 per year. However, the risk is clearly dose-related. Therefore, if a non-smoker was employed by a tavern with heavy levels of ETS, the risk might be substantially greater.
Finally, it should be noted that some findings suggest that the association between smoking and heart disease is non-linear at the very lowest exposure levels, meaning that non-smokers have a disproportionate increase in risk when exposed to ETS due to an increase in platelet aggregation.
Correlation and linear regression analysis are statistical techniques to quantify associations between an independent, sometimes called a predictor, variable (X) and a continuous dependent outcome variable (Y). For correlation analysis, the independent variable (X) can be continuous (e.g., gestational age) or ordinal (e.g., increasing categories of cigarettes per day). Regression analysis can also accommodate dichotomous independent variables.
The procedures described here assume that the association between the independent and dependent variables is linear. With some adjustments, regression analysis can also be used to estimate associations that follow another functional form (e.g., curvilinear, quadratic). Here we consider associations between one independent variable and one continuous dependent variable. The regression analysis is called simple linear regression - simple in this case refers to the fact that there is a single independent variable. In the next module, we consider regression analysis with several independent variables, or predictors, considered simultaneously.