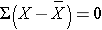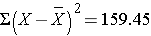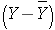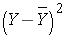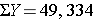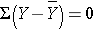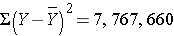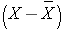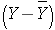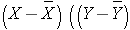Computing the Correlation Coefficient
The formula for the sample correlation coefficient is:

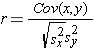
where Cov(x,y) is the covariance of x and y defined as

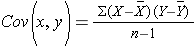

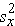 and
and 
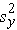 are the sample variances of x and y, defined as follows:
are the sample variances of x and y, defined as follows:

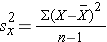 and
and 
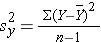
The variances of x and y measure the variability of the x scores and y scores around their respective sample means of X and Y considered separately. The covariance measures the variability of the (x,y) pairs around the mean of x and mean of y, considered simultaneously.

To compute the sample correlation coefficient, we need to compute the variance of gestational age, the variance of birth weight, and also the covariance of gestational age and birth weight.
We first summarize the gestational age data. The mean gestational age is:

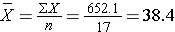
To compute the variance of gestational age, we need to sum the squared deviations (or differences) between each observed gestational age and the mean gestational age. The computations are summarized below.
|
Infant ID # |
Gestational Age (weeks) |
|
|
|---|---|---|---|
|
1 |
34.7 |
-3.7 |
13.69 |
|
2 |
36.0 |
-2.4 |
5.76 |
|
3 |
29.3 |
-9.1 |
82,81 |
|
4 |
40.1 |
1.7 |
2.89 |
|
5 |
35.7 |
-2.7 |
7.29 |
|
6 |
42.4 |
4.0 |
16.0 |
|
7 |
40.3 |
1.9 |
3.61 |
|
8 |
37.3 |
-1.1 |
1.21 |
|
9 |
40.9 |
2.5 |
6.25 |
|
10 |
38.3 |
-0.1 |
0.01 |
|
11 |
38.5 |
0.1 |
0.01 |
|
12 |
41.4 |
3.0 |
9.0 |
|
13 |
39.7 |
1.3 |
1.69 |
|
14 |
39.7 |
1.3 |
1.69 |
|
15 |
41.1 |
2.7 |
7.29 |
|
16 |
38.0 |
-0.4 |
0.16 |
|
17 |
38.7 |
0.3 |
0.09 |
|
|
|
|
|
The variance of gestational age is:

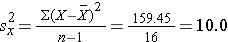
Next, we summarize the birth weight data. The mean birth weight is:

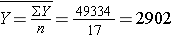
The variance of birth weight is computed just as we did for gestational age as shown in the table below.
|
Infant ID# |
Birth Weight |
|
|
|---|---|---|---|
|
1 |
1895 |
-1007 |
1,014,049 |
|
2 |
2030 |
-872 |
760,384 |
|
3 |
1440 |
-1462 |
2,137,444 |
|
4 |
2835 |
-67 |
4,489 |
|
5 |
3090 |
188 |
35,344 |
|
6 |
3827 |
925 |
855,625 |
|
7 |
3260 |
358 |
128,164 |
|
8 |
2690 |
-212 |
44,944 |
|
9 |
3285 |
383 |
146,689 |
|
10 |
2920 |
18 |
324 |
|
11 |
3430 |
528 |
278,764 |
|
12 |
3657 |
755 |
570,025 |
|
13 |
3685 |
783 |
613,089 |
|
14 |
3345 |
443 |
196,249 |
|
15 |
3260 |
358 |
128,164 |
|
16 |
2680 |
-222 |
49,284 |
|
17 |
2005 |
-897 |
804,609 |
|
|
|
|
|
The variance of birth weight is:

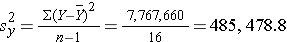
Next we compute the covariance:

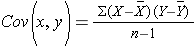
To compute the covariance of gestational age and birth weight, we need to multiply the deviation from the mean gestational age by the deviation from the mean birth weight for each participant, that is:

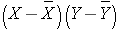
The computations are summarized below. Notice that we simply copy the deviations from the mean gestational age and birth weight from the two tables above into the table below and multiply.
|
Infant ID# |
|
|
|
|---|---|---|---|
|
1 |
-3.7 |
-1007 |
3725.9 |
|
2 |
-2.4 |
-872 |
2092.8 |
|
3 |
-9,1 |
-1462 |
13,304.2 |
|
4 |
1.7 |
-67 |
-113.9 |
|
5 |
-2.7 |
188 |
-507.6 |
|
6 |
4.0 |
925 |
3700.0 |
|
7 |
1.9 |
358 |
680.2 |
|
8 |
-1.1 |
-212 |
233.2 |
|
9 |
2.5 |
383 |
957.5 |
|
10 |
-0.1 |
18 |
-1.8 |
|
11 |
0.1 |
528 |
52.8 |
|
12 |
3.0 |
755 |
2265.0 |
|
13 |
1.3 |
783 |
1017.9 |
|
14 |
1.3 |
443 |
575.9 |
|
15 |
2.7 |
358 |
966.6 |
|
16 |
-0.4 |
-222 |
88.8 |
|
17 |
0.3 |
-897 |
-269.1 |
|
Total = 28,768.4 |
The covariance of gestational age and birth weight is:

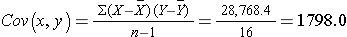
Finally, we can ow compute the sample correlation coefficient:

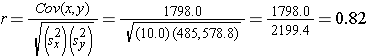
Not surprisingly, the sample correlation coefficient indicates a strong positive correlation.
As we noted, sample correlation coefficients range from -1 to +1. In practice, meaningful correlations (i.e., correlations that are clinically or practically important) can be as small as 0.4 (or -0.4) for positive (or negative) associations. There are also statistical tests to determine whether an observed correlation is statistically significant or not (i.e., statistically significantly different from zero). Procedures to test whether an observed sample correlation is suggestive of a statistically significant correlation are described in detail in Kleinbaum, Kupper and Muller.1