Population Parameters versus Sample Statistics

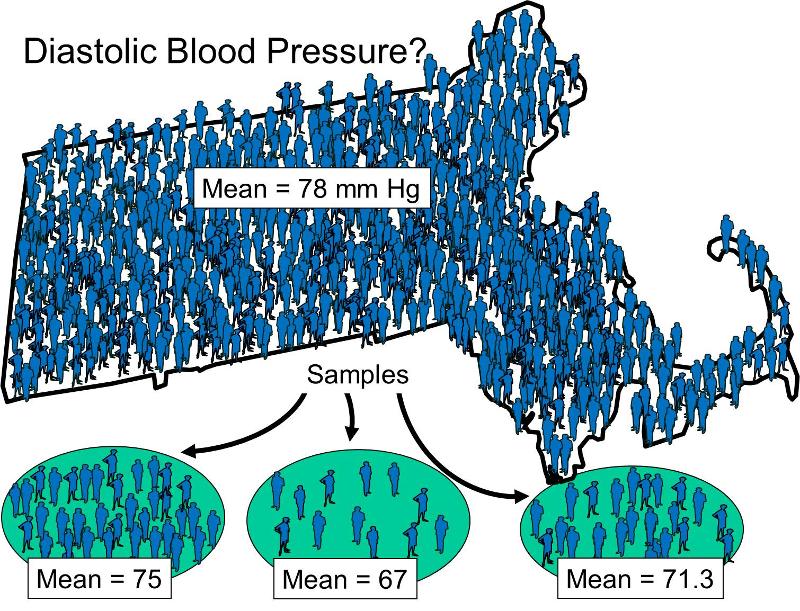
As noted in the Introduction, a fundamental task of biostatistics is to analyze samples in order to make inferences about the population from which the samples were drawn.  To illustrate this, consider the population of Massachusetts in 2010, which consisted of 6,547,629 persons. One characteristic (or variable) of potential interest might be the diastolic blood pressure of the population. There are a number of ways of reporting and analyzing this, which will be considered in the module on Summarizing Data. However, for the time being, we will focus on the mean diastolic blood pressure of all people living in Massachusetts. It is obviously not feasible to measure and record blood pressures for of all the residents, but one could take samples of the population in order estimate the population's mean diastolic blood pressure.

Map of Massachusetts with thousands of iconic people overlayed. Three random samples are drawn from the population and each sample has a slightly different mean value.

Despite the simplicity of this example, it raises a series of concepts and terms that need to be defined. The terms population, subjects, sample, variable, and data elements are defined in the tabbed activity below.

  spacer

alternative accessible content Roll over the tabs to see the definitions of these terms.
This content requires JavaScript enabled.
 

It is possible to select many samples from a given population, and we will see in other learning modules that there are several methods that can be used for selecting subjects from a population into a sample. The simple example above shows three small samples that were drawn to estimate the mean diastolic blood pressure of Massachusetts residents, although it doesn't specify how the samples were drawn. Note also that each of the samples provided a different estimate of the mean value for the population, and none of the estimates was the same as the actual mean for the overall population (78 mm Hg in this hypothetical example). In reality, one generally doesn't know the true mean values of the characteristics of the population, which is of course why we are trying to estimate them from samples. Consequently, it is important to define and distinguish between:


return to top | previous page | next page