The Criterion of Positivity
(Or the Criterion of "Normal")
One problem is that a decision must be made about what test value will be used to distinguish normal versus abnormal results. Unfortunately, when we compare the distributions of screening measurements in subjects with and without disease, we find that there is almost always some overlap, as shown in the figure to the right. Deciding the criterion for "normal" versus abnormal can be difficult.
Figure 16-5 in the textbook by Aschengrau and Seage summarizes the problem.

There may be a very low range of test results (e.g., below point A in the figure above) that indicates absence of disease with very high probability, and there may be a very high range (e.g., above point B) that indicates the presence of disease with very high probability. However, where the distributions overlap, there is a "gray zone" in which there is much less certainly about the results.
Consider the example illustrated by the next figure.
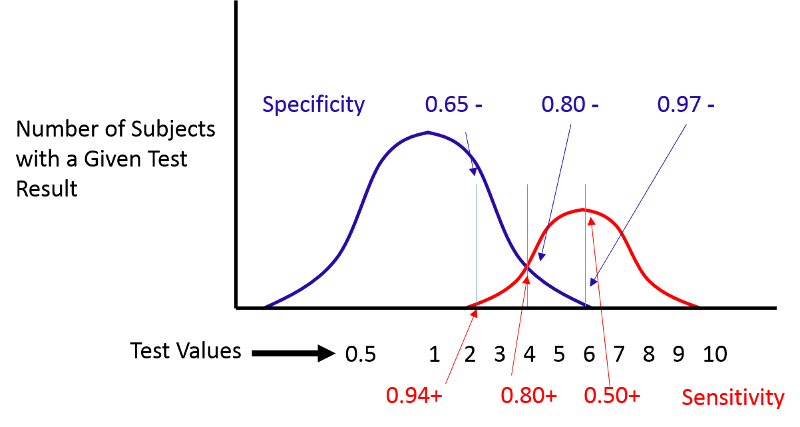
If we move the cut-off to the left, we can increase the sensitivity, but the specificity will be worse. If we move the cut-off to the right, the specificity will improve, but the sensitivity will be worse. Altering the criterion for a positive test ("abnormality") will always influence both the sensitivity and specificity of the test.
ROC Curves
(Receiver Operating Characteristic Curves)
(NOTE: You will not be tested on ROC curves in the introductory course.)
ROC curves provide a means of defining the criterion of positivity that maximizes test accuracy when the test values in diseased and non-diseased subjects overlap. As the previous figure demonstrates, one could select several different criteria of positivity and compute the sensitivity and specificity that would result from each cut point. In the example above, suppose I computed the sensitivity and specificity that would result if I used cut points of 2, 4, or 6. If I were to do this for the example above, by table would look something like this:
|
Criterion of Positivity |
Sensitivity (True Positive Rate) |
Specificity |
False Positive Rate (1-Specificity) |
|---|---|---|---|
|
2 |
0.94 |
0.65 |
0.35 |
|
4 |
0.80 |
0.80 |
0.20 |
|
6 |
0.50 |
0.97 |
0.03 |
I could then plot the true positive rate (the sensitivity) as a function of the false positive rate (1-specificity), and the plot would look like the figure below.
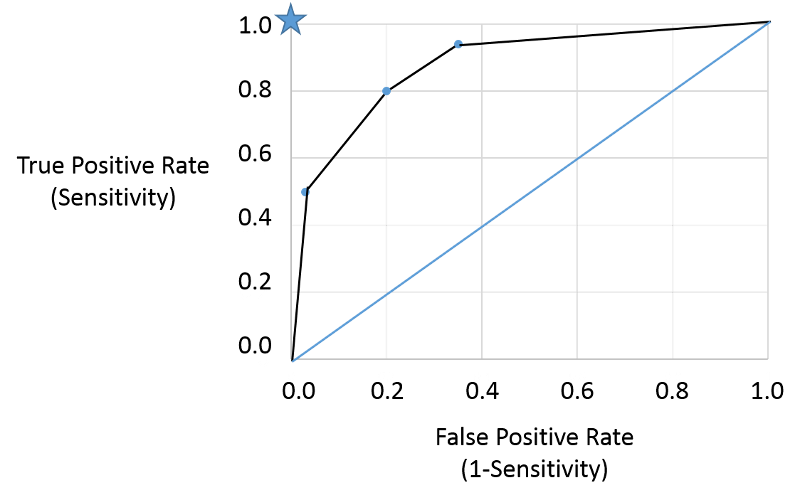
Note that the true positive and false positive rates obtained with the three different cut points (criteria) are are shown by the three blue points representing true positive and false positive rates using the three different criteria of positivity. This is a receiver-operator characteristic curve that assesses test accuracy by looking at how true positive and false positive rates change when different criteria of positivity are used. If the diseased people had test values that were always greater than the test values in non-diseased people, i.e., there were two entirely separate distributions then one could easily select a criterion of positivity that gave a true positive rate of 1 (100%) and a false positive rate of 0, as depicted by the blue star at the upper left hand corner (coordinates 0,1). The closer the ROC curve hugs the left axis and the top border, the more accurate the test, i.e., the closer the curve is to the star. The diagonal blue line illustrates the ROC curve for a useless test for which the true positive rate and the false positive rate are equal regardless of the criterion of positivity that is used - in other words the distribution of test values for disease and non-diseased people overlap entirely. So, the closer the ROC curve is to the blue star, the better it is, and the closer it is to the diagonally blue line, the worse it is.
This provides a standard way of assessing test accuracy, but perhaps another approach might be to consider the seriousness of the consequences of a false negative test. For example, failing to identify diabetes right away from a dip stick test of urine would not necessarily have any serious consequences in the long run, but failing to identify a condition that was more rapidly fatal or had serious disabling consequences would be much worse. Consequently, a common sense approach might be to select a criterion that maximizes sensitivity and accept the if the higher false positive rate that goes with that if the condition is very serious and would benefit the patient if diagnosed early.
Here is a link to a journal article describing a study looking at sensitivity and specificity of PSA testing for prostate cancer. [Richard M Hoffman, Frank D Gilliland, et al.: Prostate-specific antigen testing accuracy in community practice. BMC Family Practice 2002, 3:19]
In the video below Dr. David Felson from the Boston University School of Medicine discusses sensitivity and specificity of screening tests and diagnostic tests.