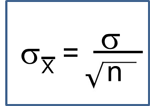Box-Whisker Plots for Continuous Variables
A popular graphical display for a continuous variable is a box-whisker plot. Outliers or extreme values can also be assessed graphically with box-whisker plots. For the subsample of n=10 Framingham participants who we considered previously we computed the following summary statistics on diastolic blood pressures:
|
Minimum: Q1: Median: Q3: Maximum: |
62 64 71 77 81 |
These are sometimes referred to as quantiles or percentiles of the distribution. A specific quantile or percentile is a value in the data set that holds a specific percentage of the values at or below it. The first quartile, for example, is the 25th percentile meaning that it holds 25% of the values at or below it. The median is the 50th percentile, the third quartile is the 75th percentile and the maximum is the 100th percentile (i.e., 100% of the values are at or below it).
A box-whisker plot is a graphical display of these percentiles. Figure 11 is a box-whisker plot of the diastolic blood pressures measured in the subsample of n=10 participants described above in Table 14. The horizontal lines represent (from the top) the maximum, the third quartile, the median (also indicated by the dot), the first quartile and the minimum. The shaded box represents the middle 50% of the distribution (between the first and third quartiles). A box-whisker plot is meant to convey the distribution of a variable at a quick glance. We determined that there were no outliers in the distribution of diastolic blood pressures in the subsample of n=10 participants who attended the seventh examination of the Framingham Offspring Study.
Figure 11 - Box-Whisker Plot of Diastolic Blood Pressures in Subsample of n=10.
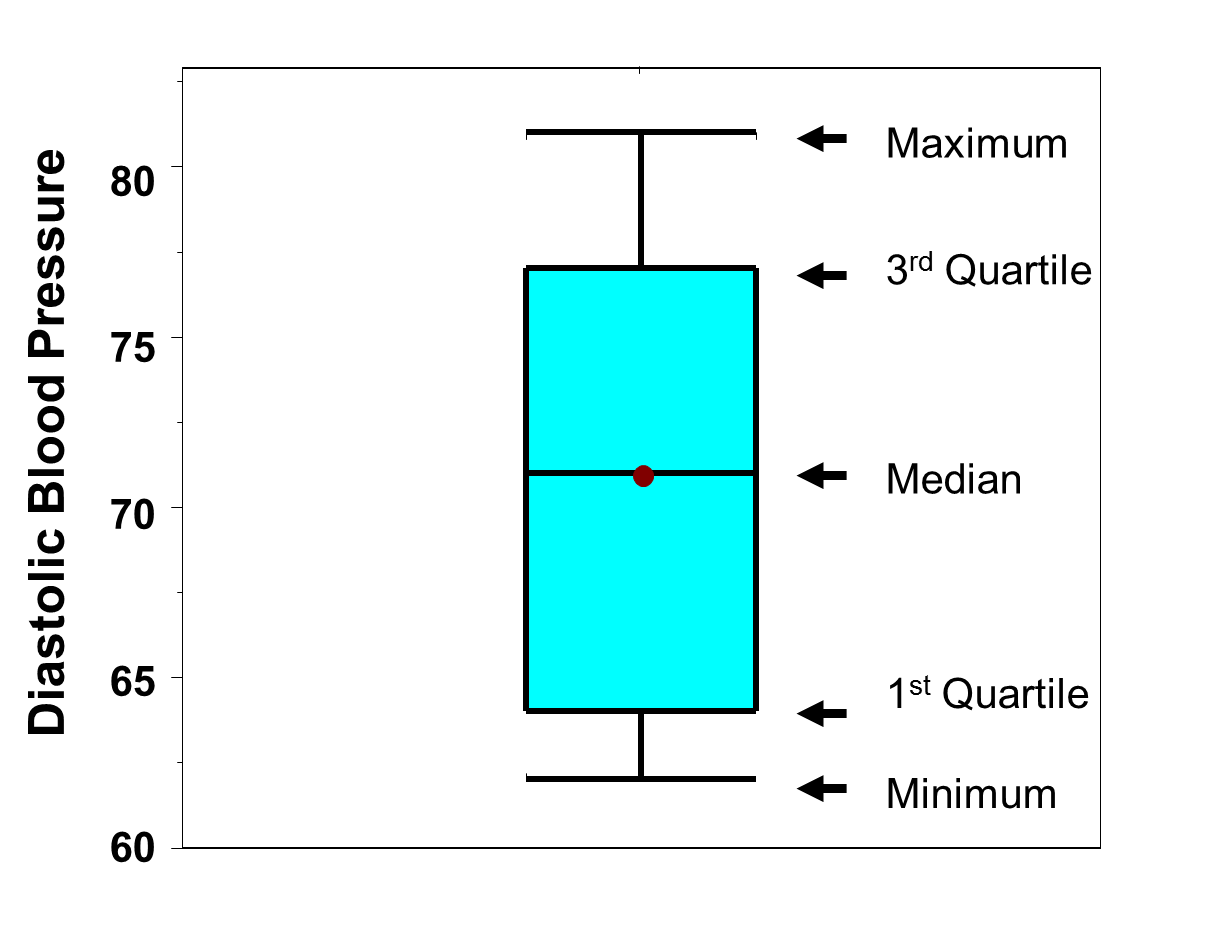
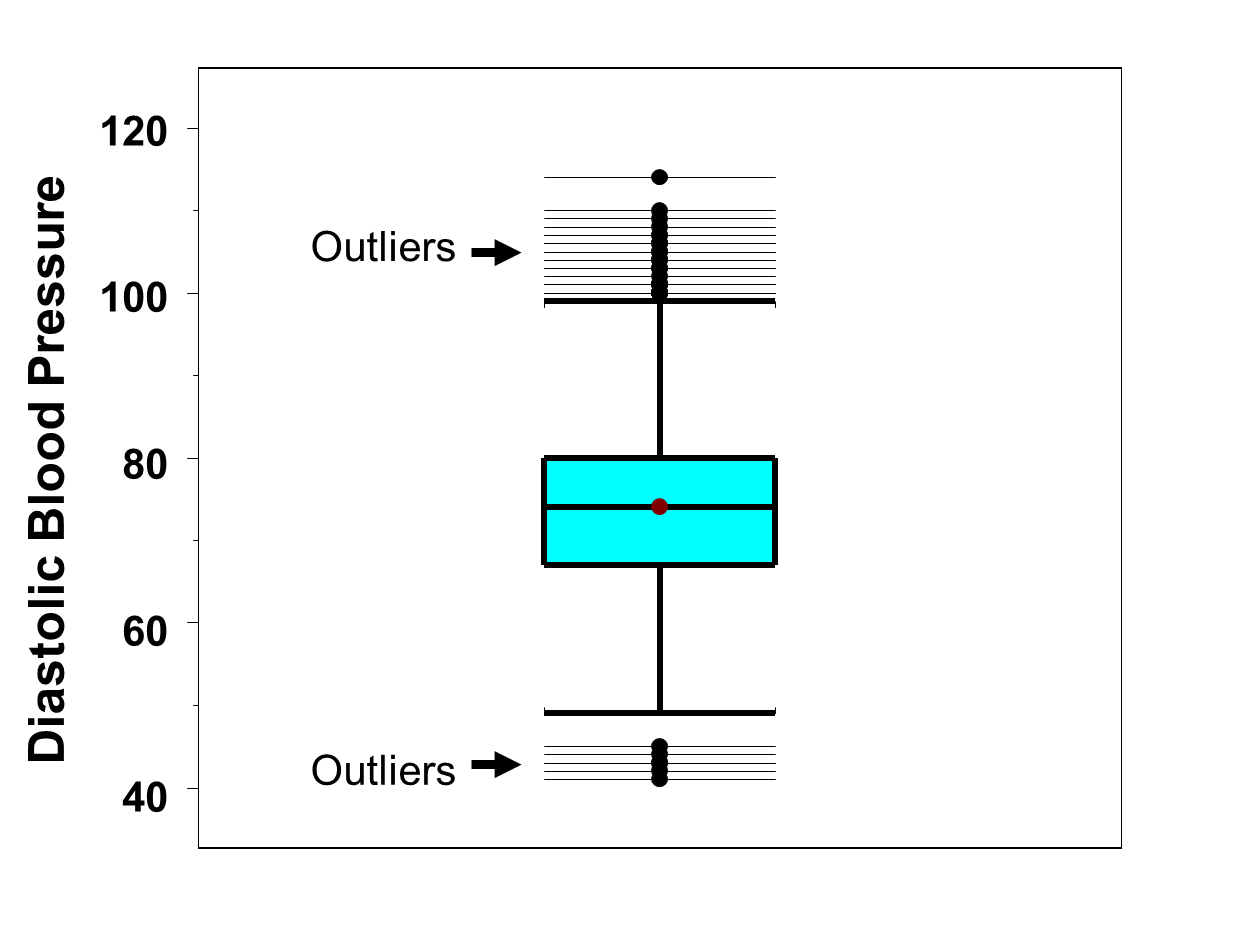
Figure 12 is a box-whisker plot of the diastolic blood pressures measured in the full sample (n=3,539) of participants. Recall that in the full sample we determined that there were outliers both at the low and the high end (See Table 16). In Figure 12 the outliers are displayed as horizontal lines at the top and bottom of the distribution. At the low end of the distribution, there are 5 values that are considered outliers (i.e., values below 47.5 which was the lower limit for determining outliers). At the high end of the distribution, there are 12 values that are considered outliers (i.e., values above 99.5 which was the upper limit for determining outliers). The "whiskers" of the plot (boldfaced horizontal brackets) are the limits we determined for detecting outliers (47.5 and 99.5).
Figure 12 - Box-Whisker Plot of Diastolic Blood Pressures with Full Sample (n=3,539) of Participants
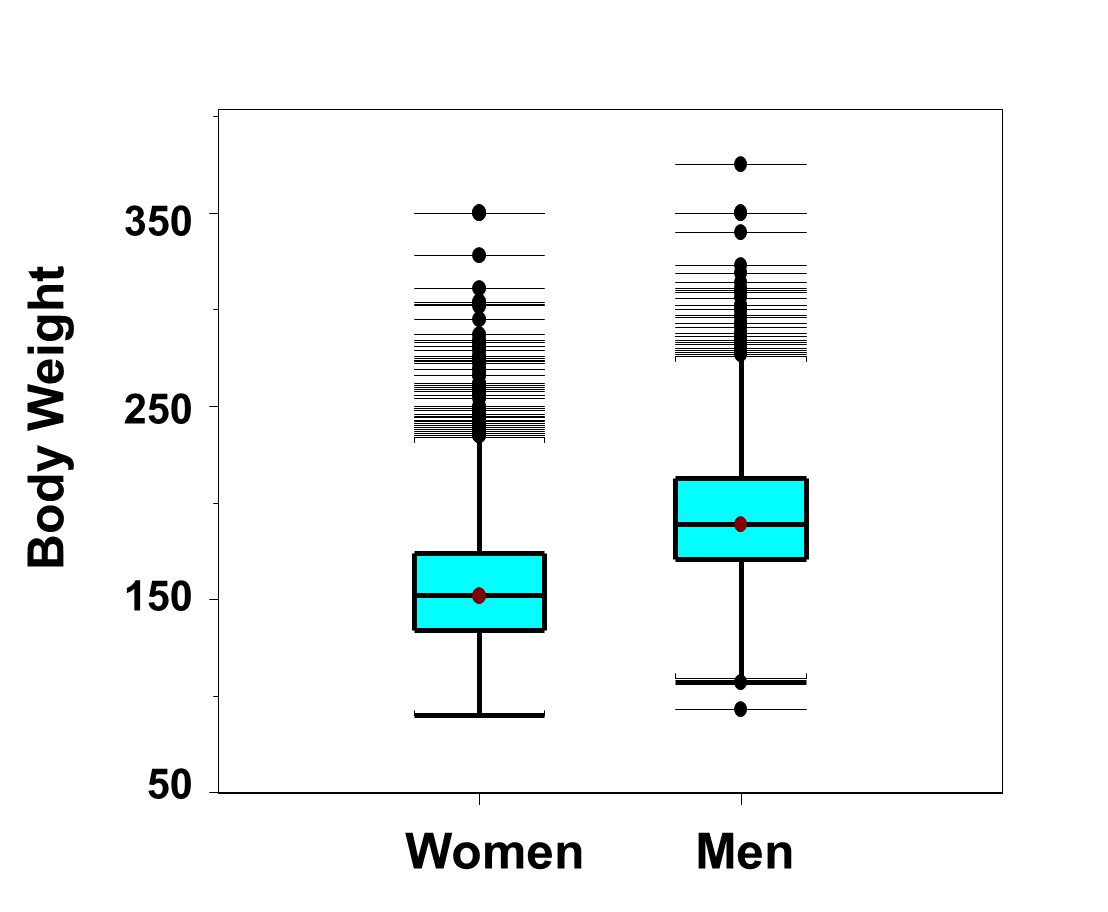
Box-whisker plots are very useful for comparing distributions. Figure 13 below shows side-by-side box-whisker plots of the distributions of weights, in pounds, for men and women in the Framingham Offspring Study. The figure clearly shows a shift in the distributions with men having much higher weights. In fact, the 25th percentile of the weights in men is approximately 180 pounds and equal to the 75th percentile in women. Specifically, 25% of the men weigh 180 or less as compared to 75% of the women. There are many outliers at the high end of the distribution among both men and women. There are two outlying low values among men.
Figure 13 - Side-by-Side Box-Whisker Plots of Weights in Men and Women in the Framingham Offspring Study
Because men are generally taller than women (see Figure 14 below), it is not surprising that men have higher weights than women.
Figure 14 - Side-by-Side Box-Whisker Plots of Heights in Men and Women in the Framingham Offspring Study
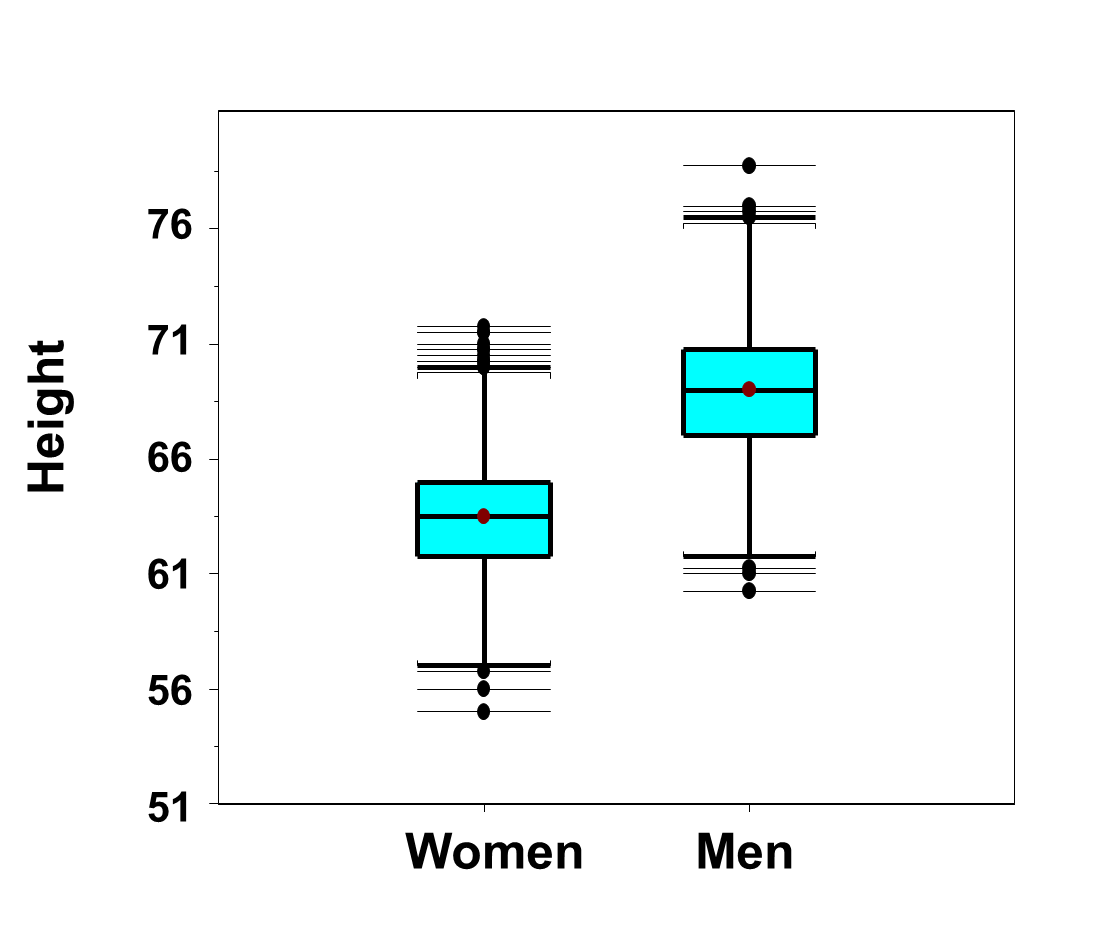
Because men are taller, a more appropriate comparison is of body mass index, see Figure 15 below.
Figure 15 - Side-by-Side Box-Whisker Plots of Body Mass Index in Men and Women in the Framingham Offspring Study
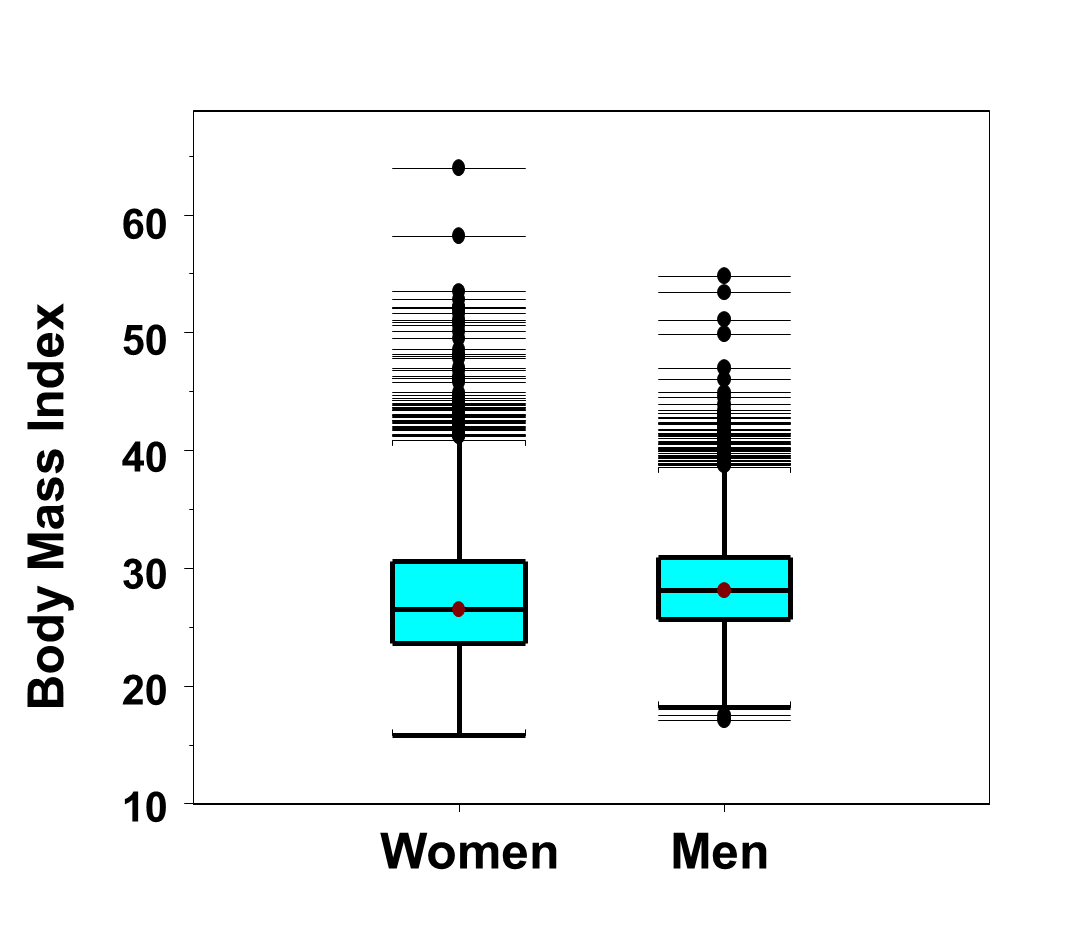
The distributions of body mass index are similar for men and women. There are again many outliers in the distributions in both men and women. However, when taking height into account (by comparing body mass index instead of comparing weights alone), we see that the most extreme outliers are among the women.

In the box-whisker plots, outliers are values which either exceed Q3 + 1.5 IQR or fall below Q1- 1.5 IQR. Some statistical computing packages use the following to determine outliers: values which either exceed Q3 + 3 IQR or fall below Q1- 3 IQR, which would result in fewer observations being classified as outliers.7,8 The rule using 1.5 IQR is the more commonly applied rule to determine outliers.